Einführung in die Integralrechnung

Lernpfad

In diesem Lernpfad können die Schüler die grundlegenden Zusammenhänge der Integralrechnung anhand vieler interaktiver Übungen entdecken.

Einige Übungen sind dem gleichnamigen Lernpfad Einführung in die Integralrechnung der österreichischen Arbeitsgruppe Medienvielfalt im Mathematikunterricht entnommen, die aus einer Kooperation von mathe-online und GeoGebra entstanden ist.

Voraussetzungen:
Zeitbedarf: etwa 3 Schulstunden

Materialien: Das bestimmte Integral;  Aufgaben mit Lösung;  Integralfunktion

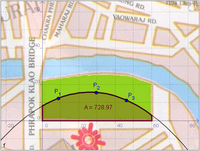
Das Flächenproblem

Ziel der folgenden Überlegungen ist es, ein Verfahren zu entwickeln, mit dem Flächeninhalte von krummlinig begrenzten Flächen berechnet werden können. Wie groß ist der Wasserverbrauch? Wie groß ist der Flächeninhalt des Grundstücks?

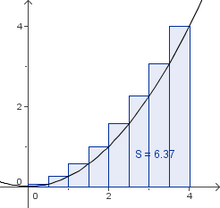
Unter- und Obersumme

• Begriffsklärung Unter- und Obersumme
• Aufgabe: Gegeben ist die Funktion f(x) = 0.25 x².

1. Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft.
2. Berechne die zugehörige Ober- und Untersumme.
3. Gib auch das arithmetische Mittel von Ober- und Untersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an.
4. Lösung:

x

0

0,5

1,5

2

2,5

3

3,5

4

f(x)

0

x

0,0625

0,25

1,5

2

2,5

3

3,5

4

1,5

2

2,5

3

3,5

4

Für den Flächeninhalt der Obersumme gilt:
S = f (0,5) $\cdot$ 0,5 + f (1) $\cdot$ 0,5 + .....f (4) $\cdot$ 0,5 = 0,5 $\cdot$f(0,5) + f(1) + ...f (4) = 6,375

Für den Flächeninhalt der Untersumme gilt:
s = f (0) $\cdot$ 0,5 + f (0,5) $\cdot$ 0,5 + .....f (3,5) $\cdot$ 0,5 = 4,375

Mittelwert: 5,375

• Berechnung von Unter- und Obersummen mit GeoGebra

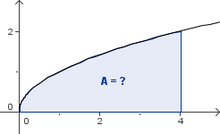
Das bestimmte Integral

• Informiere dich im  Arbeitsblatt "Das bestimmte Integral" über die Definition des Begriffs "bestimmtes Integral".
• Auf dem  Arbeitsblatt sind für einige einfache Funktionen die bestimmten Integrale über dem Intervall [a;b] angegeben. Finde anschauliche Erklärungen für die Herleitung und berechne die bestimmten Integrale für die angegeben Werte!  Lösung
• Berechne: $\int_{0}^{3}(x^2-2x-3)\, \mathrm{d}x$; $\int_{1}^{4}(x^2-2x-3)\, \mathrm{d}x$; $\int_{4}^{1}(x^2-2x-3)\, \mathrm{d}x$
• Überprüfe die Lösung mit folgendem Applet, in dem du mit Hilfe der Schieberegler die Integrationsgrenzen anpasst!

Flächenberechnung

• Aufgaben zur Flächenberechnung mit Geogebra
• Kläre die Bedeutung des Begriffs "negativer Flächeninhalt"!
• Erkläre den Unterschied zwischen dem Wert des bestimmten Integrals und dem Flächeninhalt zwischen Graph und x-Achse!

Integralfunktion

• Bearbeite die Punkte 1 bis 6 des dynamischen Arbeitsblatts zur Integralfunktion. Halte die Ergebnisse in deinem Heft fest.
• Überlege: Welche Funktionen der Kurvenschar sind keine Integralfunktionen?
• Bearbeite nun als Zusammmenfassung das  Arbeitsblatt "Die Integralfunktion".

Zusätzliche Übungsaufgaben

• Integration mit unbekannten Grenzen

Für Interessierte

• Hauptsatz der Differential- und Integralrechnung mit ausführlichem Beweis

• Informiere dich im Internet über die Geschichte der Integralrechnung.
• Bei welchen Fragestellungen kommt die Integralrechung zum Einsatz? Finde möglichst vielfältige Beispiele.

<metakeywords>ZUM2Edutags,ZUM-Wiki,Mathematik-digital,Einführung in die Integralrechnung,Mathematik,Einführung,Integralrechnung,12. Klasse,Oberstufe,Lernpfad</metakeywords>