Einführung in die Differentialrechnung

Lernpfad

Im bisherigen Mathematikunterricht wurden bereits vielfach Funktionen und deren Wertetabellen und Graphen betrachtet. Allerdings wurde das Änderungsverhalten von Funktionen bisher nur eingeschränkt untersucht, obwohl es eine essentielle Eigenschaft von Funktionen ist.

Am Ende des 17. Jahrhunderts gingen Gottfried Wilhelm Leibniz und Isaac Newton der mathematischen Bestimmung des Änderungsverhaltens von Funktionen genauer nach und entwickelten Ideen, auf deren Grundlage die Differentialrechnung entwickelt wurde. Die Differentialrechnung war ein wichtiger Baustein in der Weiterentwicklung der Mathematik und der Naturwissenschaften und ist heute eine unverzichtbare Methode in der Mathematik.

Im folgenden Lernpfad lernen Sie die Ideen von Leibniz und Newton kennen. Sie lernen dabei die grundlegenden Begriffe der Differentialrechnung wie mittlere und momentane Änderungsrate, Steigung, Sekante, Tangente, Differenzenquotient, Differentialquotient und Ableitung kennen.
Zur erfolgreichen Bearbeitung sollten Sie vertraut mit der Theorie der linearen Funktionen sein. Sie sollten insbesondere wissen, was die Steigung einer linearen Funktion ist und wie man sie bestimmt.

Zur Dokumentation Ihres Lernprozesses sollen Sie die Aufgaben des Lernpfades in einer Mappe oder einem Heft nachvollziehbar aufschreiben.

Die didaktischen Gestaltungselemente dieses Lernpfad werden im Abschnitt 8 des Buchs Medienvielfalt im Mathematikunterricht, Jürgen Roth, Evelyn Süss-Stepancik, Heike Wiesner (Hrsg.), Springer Spektrum 2015, ISBN 978-3-658-06448-8 beschrieben.

Einstiegsaufgabe 1 - Blumenvase

Unterschiedliche Gefäßformen lassen sich durch ihren Füllgraphen beschreiben. Dieser ergibt sich, wenn in ein Gefäß eine Flüssigkeit mit gleichmäßigem Zufluss einfließt. Die entstehende Zuordnung Zeit(t) -> Höhe(h) kann in ein Koordinatensystem übertragen werden und stellt die Zunahme des Wasserspiegels in Abhängigkeit von der Zeit dar.

Experiment

Skizzieren Sie zunächst einen möglichen Verlauf des Füllgraphen für die Gefäße in ein Koordinatensystem. Vergleichen Sie Ihre Ergebnisse mit einer anderen Zweiergruppe und begründen Ihre Skizze.

Mit dem folgenden Experiment können Sie Ihre Vermutung aus der ersten Aufgabe überprüfen. Dazu sollen Sie gleichmäßig Wasser in ein Gefäß füllen. Mit einer Stoppuhr wird die Zeit gemessen, wie lange der Wasserspiegel braucht um auf 0.5 cm, 1 cm, 1.5 cm, 2cm usw. zu steigen. Die Messdaten für die Zeit übertragen Sie danach vom Arbeitsblatt in die untenstehende GeoGebra-Tabelle.

Benötigte Materialien:

• Messbecher
• Einfülltrichter
• Höhenskala
• Stoppuhr (z.B. App im Smartphone)
• leere Plastikflasche 500ml

Im Bild sehen Sie den Versuchsaufbau. Bei der Versuchsdurchführung ist es zum einen besonders wichtig, dass der Wasserzufluss immer gleichmäßig ist. Der obere Teil des Trichters muss daher immer mit Wasser gefüllt sein, sodass der Zufluss konstant bleibt. Zum anderen muss der „Zeitmesser“ genau beobachten, wann der Wasserspiegel die markierten Höhen erreicht, damit die Messung so exakt wie möglich ist.

Achtung: Bei manchen Stoppuhren lassen sich Zwischenzeiten stoppen. Diese liefern für unseren Versuch die genaueren Ergebnisse, müssen aber zunächst noch addiert werden.

Wenn alle Messdaten in der Tabelle eingetragen sind, können Sie sich die dazugehörigen Punkte im Koordinatensystem anzeigen lassen. Markieren Sie als erstes alle Messwerte (Zeit und Höhe). Durch einen Rechtsklick über den markierten Werten kann im erscheinenden Kontextmenü Erzeuge - Liste von Punkten ausgewählt werden, sodass die zu den Messwerten gehörigen Punkte im Koordinatensystem erscheinen.

Aufgabe 1

a) Vergleichen Sie die Versuchsdaten mit ihren Skizzen und beschreiben den Verlauf des Füllgraphen. Inwiefern kann man die Form des Gefäßes am Füllgraphen ablesen?

b) Um weitere Erkenntnisse über den Füllvorgang zu erhalten soll nun die Geschwindigkeit des Anstiegs des Wasserspiegels untersucht werden. Ist es möglich, diese Geschwindigkeit zum Zeitpunkt $t = 3s$ zu ermitteln? Begründen Sie ihre Antwort kurz.

Einstiegsaufgabe 2 - Barringer-Krater

Die Idee zu dieser Aufgabe entstammt dem Schulbuch Lambacher-Schweizer, Analysis Leistungskurs Gesamtband, Ausgabe A, Klett Verlag, Stuttgart 2001, ISBN 3127321805.

Barrington-Krater

In Arizona gibt es einen Einschlagskrater eines Meteoriten, den sogenannten Barringer-Krater. Der Krater hat einen Durchmesser von bis zu 1200 Meter und eine Tiefe von 180 Meter. An einer sehr flachen Stelle kann der Teilquerschnitt des Kraters bis zum Rand durch die Funktion $k(x)=0,002x^2$ für $0 \leq x \leq 300$ beschrieben werden.

Aufgabe 2

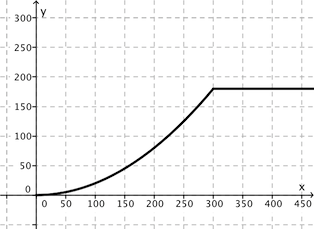
Im Krater befindet sich ein Fahrzeug, das eine Steigung von bis zu 115% bewältigen kann. Kann das Fahrzeug den Kraterrand erreichen und aus dem Krater herausfahren?

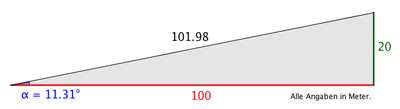
Wird eine Steigung, wie z.B. bei einem Verkehrschild angegeben, so bedeutet die Prozentangabe eine Höhenveränderung von 20m je 100m horizontaler Strecke. Im nachstehenden Bild finden Sie die genauen Angaben. Beachten Sie insbesondere auch die Länge der tatsächlich zurückgelegten Strecke je 100m, sowie den realen Winkel der Höhenänderung.

Arbeitsblätter zu den Einstiegsaufgaben

Vorwissenstest

Vor der Bearbeitung der weiteren Aufgaben sollten Sie in einem kurzen Vorwissenstest überprüfen, ob Sie mit für die weitere Arbeit benötigten Rechnungen vertraut genug sind.

1a) Gegeben ist die Funktion f(x) = 2x+1. Welchen Wert hat f(3)? (!1) (!3) (!5) (7) (!9)

1b) Die Rechenvorschrift $t(v) = \frac{100}{v}$ gibt an, wie viele Stunden t man für 100 km bei einer bestimmten Geschwindigkeit v (in km/h) benötigt. Welchen Wert hat t(50)? (2) (!1) (!3) (!4) (!5) (!50) (!100)

1c) Für die Rechenvorschrift aus 1b gilt: t(25) = 4. Was bedeutet das? (Für 100 km benötigt man 4 Stunden bei 25 km/h) (!Für 25 Kilometer benötigt man 1/4 Stunde bei 100 km/h) (!Für 4 Kilometer benötigt man 25 Sekunden bei 100 km/h)

1d) Wenn man einen Gegenstand von z.B. einem Turm fallen lässt, kann die Fallstrecke s (in Meter) näherungsweise mit der Formel s(t) = 5t² beschrieben werden, wobei t die Fallzeit in Sekunden angibt. Um wie viel Meter fällt ein Gegenstand zwischen Sekunde 1 und 2? (15 Meter) (!5 Meter) (!10 Meter) (!20 Meter) (!25 Meter)

Wenn deine Lösungsrate mindestens 75% beträgt, gehe zu den weiteren Aufgaben. Wenn du weniger als 75% richtig hast, schaue dir das folgende Video an, bearbeite die Testaufgaben erneut und finde deine Fehler in den Testaufgaben:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Von der mittleren zur momentanen Änderungsrate

Für diesen Abschnitt haben Sie 60 Minuten Zeit.

In diesem Abschnitt soll die erste Einstiegsaufgabe, die Sie im Unterricht bearbeitet haben, vertieft werden. Sie üben, mittlere Änderungsraten zu bestimmen und damit momentane Änderungsraten anzunähern.

Blumenvase

In der Einstiegsaufgabe haben Sie in Gefäßen gleichmäßig Wasser eingelassen und die Höhe des Wasserstandes gemessen. Betrachten wir nun die abgebildete Vase, in die ebenfalls gleichmäßig Wasser eingelassen wird. Die Tabelle stellt dar, wie sich die Wasserhöhe (hier gemessen vom Tischboden) in der Vase beim Einfüllvorgang im Zeitverlauf verändert. Im Gegensatz zum Vorgehen zur Einstiegsaufgabe wurde nun alle drei Sekunden die Höhe des Wasserstandes gemessen.

Zeit (Sekunden)	Höhe (cm)
0	0,51
3	1,33
6	2,74
9	4,91
12	8,00
15	12,17
18	17,58

Mittlere Änderungsrate

Die mittlere Änderungsrate gibt an, wie viel Zentimeter pro Sekunde die Wasserhöhe in einem Zeitabschnitt im Schnitt zunimmt.

Bsp.
In den drei Sekunden zwischen Sekunde 6 und 9 steigt das Wasser um 4,91 cm - 2,74 cm = 2,17 cm. Daher nimmt das Wasser pro Sekunde um 2,17 cm : 3 s = 0,72 cm/s zu. Die mittlere Änderungsrate im Zeitabschnitt von Sekunde 6 und Sekunde 9 beträgt daher 0,72 cm pro Sekunde (abgekürzte Schreibweise: 0,72 cm/s)

Aufgabe 3

Berechnen Sie anhand der obigen Tabelle und mit dem Taschenrechner die mittlere Änderungsrate in den angegebenen Zeitabschnitten:
a) in den ersten drei Sekunden
b) zwischen Sekunde 3 und 6
c) zwischen Sekunde 12 und 15
d) zwischen Sekunde 3 und 12
e) in den ersten 18 Sekunden

a) 0,273 cm/s
b) 0,47 cm/s
c) 1,39 cm/s
d) 0,741 cm/s.

e) 0,948 cm/s

a) In den ersten drei Sekunden steigt die Wasserhöhe um 1,33 cm - 0,51 cm = 0,82 cm. Pro Sekunde steigt es daher um 0,82 cm : 3 s = 0,273 cm/s.
b) In den drei Sekunden von Sekunde 3 auf Sekunde 6 nimmt die Wasserhöhe um 2,74 cm - 1,33 cm = 1,41 cm zu. Die mittlere Änderungsrate ist daher 1,41 cm : 3 s = 0,47 cm/s.
c) Zwischen Sekunde 12 und 15 liegen wiederum 3 Sekunden. In diesem Zeitraum steigt das Wasser um 12,17 cm - 8 cm = 4,17 cm. Pro Sekunde nimmt das Wasser in diesem Zeitraum daher um 4,17 cm : 3 s = 1,39 cm/s zu.
d) Bei Sekunde 3 beträgt die Wasserhöhe 1,33 cm, während sie bei Sekunde 12 genau 8 cm beträgt. In diesen 9 Sekunden ist die Wasserhöhe also um 8 cm - 1,33 cm = 6,67 cm gesteigen. Die mittlere Änderungsrate zwischen Sekunde 3 und 12 beträgt daher 6,67 cm : 9 s = 0,741 cm/s.

e) Das Wasser nimmt in den ersten 18 Sekunden um 17,58 cm - 0,51 cm = 17,07 cm zu. Die mittlere Änderungsrate beträgt in diesem Zeitintervall daher 17,07 cm : 18 s = 0,948 cm/s.

Momentane Änderungsrate

Möchte man nun für einen Zeitpunkt (z.B. Sekunde 12) eine Änderungsrate bestimmen, so spricht man von der momentanen Änderungsrate. Wie man die momentane Änderungsrate näherungsweise bestimmen kann, erfahren Sie in der folgenden Aufgabe.

Aufgabe 4

Um näherungsweise die momentane Änderungsrate für den Zeitpunkt t₀ = 12 Sekunden zu erhalten, bestimmen Sie mit Hilfe der Schieberegler des Applets und mit Hilfe des Taschenrechners die mittlere Änderungsrate im Zeitintervall von ...
a) ... t₀ = 12 Sekunden und t₁ = 13 Sekunden
b) ... t₀ = 12 Sekunden und t₁ = 12,5 Sekunden
c) ... t₀= 12 Sekunden und t₁= 12,1 Sekunden
d) ... t₀ = 12 Sekunden und t₁ = 12,05 Sekunden
e) Schätzen Sie aufgrund der Ergebnisse aus a) - d), welches Ergebnis für die momentane Änderungsrate bei Sekunde 12 Ihnen plausibel erscheint.

a) 1,261 cm/s.
b) 1,2302 cm/s
c) 1,206 cm/s
d) 1,204 cm/s

e) 1,2 cm/s

a) Bei Sekunde 12 beträgt die Wasserhöhe genau 8 cm, während das Wasser bei Sekunde 13 die Höhe 9,261 cm hat. In der einen Sekunden ist es also um 9,261 - 8 cm = 1,261 cm gestiegen. Die mittlere Änderungsrate in diesem Zeitabschnitt beträgt daher 1,261 cm/s.
b) 8,6151 cm - 8 cm = 0,6151 cm => 0,6151 cm : 0,5 s = 1,2302 cm/s
c) 1,206 cm/s
d) 1,204 cm/s

e) Der Wert scheint sich dem Wert 1,2 cm/s anzunähern; man sagt, der Wert strebt gegen 1,2 cm/s.

Wenn der Wasserstand als Funktion von der Zeit mit einer Funktionsvorschrift gegeben ist, kann man die mittleren Änderungsraten auch rechnerisch bestimmen.

Aufgabe 5

Die Höhe des Wasserstandes der bisher betrachteten Vase kann mit der Funktion w(t)=0,001(t+8)³ beschrieben werden. Hierbei gibt w(t) die Höhe des Wasserstandes in cm zu einem Zeitpunkt t (in Sekunden) an.
a) Bestimmen Sie den Näherungswert für die momentane Änderungsrate noch genauer, indem Sie mit Hilfe der Funktionsvorschrift die mittlere Änderungsrate im Zeitabschnitt von Sekunde 12 bis 12,001 bestimmen.
b) Beschreiben Sie, wie Sie vorgehen müssten, um einen möglichst exakten Wert für die momentane Änderungsrate bei Sekunde 12 zu erhalten.

Die Höhe des Wasserstands zu einem Zeitpunkt kann bestimmt werden, indem der Zeitpunkt in die Funktionsvorschrift eingesetzt wird, z. B. wird der Wasserstand zu Zeitpunkt t=12 Sekunden bestimmt durch $w(12)=0,001(12+8)^3=0,001*20^3=8$.

a) 1,20006 cm/s

a)
$w(12)=0,001(12+8)^3=8$
$w(12,001)=0,001(12,001+8)^3=8,00120006$
=> Höhenzunahme: $8,00120006 cm - 8 cm = 0,00120006 cm$
=> mittlere Änderungsrate: $0,00120006 cm : 0,001 s = 1,20006 cm/s$

b) Der Zeitabschnitt für die mittlere Änderungsrate müsste immer kleiner gewählt werden, z.B. zwischen Sekunde 12 und 12,00001 usw.

Hausaufgaben:

• Seite 155/6, Seite 156/7 (Bigalke-Köhler, Mathematik 1, Hessen, Cornelsen-Verlag 2009, ISBN 978-3-464-57449-2) bzw.
• Seite 40/6, Seite 41/7 (Bigalke-Köhler, Mathematik Band 1, Analysis, Cornelsen-Verlag 2007, ISBN 978-3-06-000478-2) bzw.
• Seite 41/2, Seite 45/1c, Seite 45/3 (Lambacher-Schweizer, Mathematik Leistungskurs, Klett-Verlag 2011, ISBN 978-3-12-735601-4)

Testen

Sie sollten nach dem Test sagen können:

Ich kann mittlere Änderungsraten bestimmen, wenn die Werte in einer Wertetabelle vorliegen oder die Funktionsvorschrift gegeben ist.
Ich kann mit mittleren Änderungsraten die momentane Änderungsrate annähern.

Aus technischen Gründen werden an manchen Stellen bei den Aufgaben eckige Klammern statt der in diesem Zusammenhang sonst üblichen runden Klammern verwendet.

1a) Mit 10 Jahren war Peter 141 cm groß. Mit 12 Jahren war er 149 cm. Mit welcher mittleren Änderungsrate ist Peter während der zwei Jahre gewachsen? (4 cm/Jahr) (!8 cm/Jahr) (!2 cm/Jahr) (!6 cm/Jahr) (!10 cm/Jahr)

1b) Ein Auto beschleunigt von 0 auf 100 gemäß der Formel s[t]=1,5t², wobei s[t] die zurückgelegte Strecke zu einem bestimmten Zeitpunkt t in Sekunden angibt. Sara möchte einen möglichst guten Näherungswert für die momentane Änderungsrate zum Zeitpunkt t=4 Sekunden berechnen. Welche beiden der folgenden Funktionswerte sollte sie dafür verwenden? (s[4]) (!s[4,01]) (!s[4,05]) (!s[4,001]) (s[4,0001]) (!s[4,5])

1c) Beziehen sich die folgenden Aussagen auf die mittlere oder die momentane Änderungsrate?

"Ich bin mit 110km/h geblitzt worden, wo nur 80 km/h erlaubt waren!" (Momentane Änderungsrate) (!Mittlere Änderungsrate)

"Unsere Sonnenblumen im Garten sind im letzten Monat durchschnittlich 1cm am Tag gewachsen." (!Momentane Änderungsrate) (Mittlere Änderungsrate)

"Bei unserer Hinfahrt zum Urlaub waren wir im Schnitt nur mit 80 km/h unterwegs, da die Autobahn so überfüllt war." (!Momentane Änderungsrate) (Mittlere Änderungsrate)

"Der ICE hat eine Höchstgeschwindigkeit von 330 km/h." (Momentane Änderungsrate) (!Mittlere Änderungsrate)

Wenn Ihre Lösungsrate mindestens 75% beträgt, gehen Sie zu den weiteren Aufgaben. Wenn Sie weniger als 75% richtig haben, überprüfen Sie genau Ihre Fehler und versuchen Sie zu verstehen, was Sie falsch gemacht haben.

Von der Sekanten- zur Tangentensteigung

Für diesen Abschnitt haben Sie 60 Minuten Zeit.

In diesem Abschnitt soll die zweite Einstiegsaufgabe, die Sie im Unterricht bearbeitet haben, vertieft und verallgemeinert werden. Sie lernen und üben, Sekantensteigungen und Tangentensteigungen zu bestimmen.

Barringer-Krater

Um entscheiden zu können, ob das Raumfahrzeug aus dem Krater kommt, benötigen wir die Steigung des Kraters am Rand des Kraters.
Die durchschnittliche Steigung des Kraters zwischen zwei Punkten $A\left( x_0 | k(x_0) \right)$ und $B\left( x_1 | k(x_1) \right)$ kann mit $m=\frac{\Delta y}{\Delta x}=\frac{k(x_1)-k(x_0)}{x_1-x_0}$ berechnet werden. Dies enspricht der Steigung der Geraden, die durch die Punkte A und B geht.

Eine solche Gerade, die den Graphen einer Funktion k(x) in zwei Punkten $A\left( x_0 | k(x_0) \right)$ und $B\left( x_1 | k(x_1) \right)$ schneidet, nennt man Sekante.

$m=\frac{\Delta y}{\Delta x}=\frac{k(x_1)-k(x_0)}{x_1-x_0}$ ist dann die Sekantensteigung.

Aufgabe 6

Überlegen Sie, wo in der Zeichnung folgende Größen zu finden sind: $x_1-x_0$ und $k(x_1)-k(x_0)$

Achtung: Nicht auf den Monitor malen;-)

Lösung mit Beschriftung

Aufgabe 7

Berechnen Sie die durchschnittliche Steigung des Kraters zwischen den Punkten A(300|180) und B(400|320), wenn man sich das Kraterprofil über den Wert x₀ hinaus fortgesetzt denkt.

$m=\frac{320-180}{400-300}=\frac{140}{100}=1,4$

Dieser Wert ist größer als 1,15. Das heißt, dass das Raumfahrzeug diese Steigung nicht mehr bewältigen kann. Es ist aber auch nur die durchschnittliche Steigung zwischen den Punkten A und B und nicht die Steigung im Punkt A, die für das Herauskommen des Fahrzeugs interessant ist.

Information
Eine Sekante schneidet den Graphen in zwei Punkten. Wenn nun der Punkt B immer weiter dem Punkt A angenähert wird und bei diesem Prozess letztendlich der Punkt B mit dem Punkt A zusammenfällt, so berührt die Gerade (lokal) den Graphen nur noch in einem Punkt, dem sogenannten Berührpunkt. Diese Gerade nennt man nun nicht mehr Sekante (da es keine zwei Schnittpunkte mehr gibt), sondern Tangente an den Graphen der Funktion k im Punkt A. Die Steigung der Tangenten gibt die Steigung des Graphen der Funktion im Berührpunkt an. Wenn die Steigung der Tangenten positiv ist, steigt der Graph, wenn sie negativ ist, bedeutet dies, dass der Graph in diesem Punkt fällt.

In der Graphik der Lösung der Aufgabe 6 kann man den Punkt B bewegen, indem man mit der Maus auf ihn zeigt und bei gedrückter linker Maustaste die Maus bewegt.

Aufgabe 8

Vollziehen Sie den beschriebenen Übergang von der Sekante zur Tangente im obigen Applet nach.

Berechnen Sie die Steigungen verschiedener Sekanten mit Hilfe der Werte, die Sie für $\Delta x$ und $\Delta y$ aus dem Applet entnehmen können.

Was können Sie nun über die Steigung im Punkt A sagen?

Um zu entscheiden, ob das Fahrzeug aus dem Krater heraus kommt, muss ein genauer Wert für die Steigung der Tangenten an den Graphen im Punkt A betrachtet werden. Wenn die Steigung des Kraters im Punkt A(300|180) kleiner als 1,15 ist, kann das Raumfahrzeug den Krater verlassen.

Die weiteren Betrachtungen führen wir nun etwas allgemeiner auch für andere Funktionen durch, bevor wir die Steigung im Punkt A des Kraters tatsächlich berechnen.

Verallgemeinerung

Die Überlegungen, die wir für die Kraterfunktion angestellt haben, kann man auch für andere Funktionen durchführen.

Aufgabe 9

Auf dem Arbeitsblatt, das am Pult liegt, ist der Graph der Funktion f mit $f(x)=x^2$ gezeichnet.
a) Zeichnen Sie die Sekante durch die Punkte A(1|f(1)) und B(2|f(2)) und bestimmen Sie aus der Zeichnung ihre Steigung.
b) Zeichnen Sie ebenso die Sekante durch die Punkte A(1|f(1)) und C(1,5|f(1,5)) und bestimmen Sie aus der Zeichnung ihre Steigung.
c) Zeichnen Sie (näherungsweise) die Tangente an den Graphen im Punkt A(1|1) ein und bestimmen Sie ihre Steigung aus der Zeichnung.

a) Die Steigung ist (ungefähr) 3.
b) Die Steigung ist (ungefähr) 2,5.

c) Die Steigung ist (ungefähr) 2.

Aufgabe 10

Wir betrachten weiterhin die Funktion f mit $f(x)=x^2$.
a) Bestimmen Sie rechnerisch für die Werte $x_0=1$ und $x_1=2$ mit Hilfe der Formel $m=\frac{f(x_1)-f(x_0)}{x_1-x_0}$ die Steigung der Sekante durch die Punkte A(1|f(1)) und B(2|f(2)). Vergleichen Sie mit dem Ergebnis aus der vorherigen Aufgabe.
b) Näheren Sie nun die Steigung der Tangenten im Punkt A(1|1) an den Graphen besser an, indem Sie für x₁ einen Wert wählen, der näher an x₀ liegt. Vergleichen Sie mit Ihrem Ergebnis aus der vorherigen Aufgabe.
c) Überlegen Sie, wie man einen möglichst genauen Wert für die Steigung der Tangenten erhalten kann.

a) Die Steigung ist $m=\frac{4-1}{2-1}=3$.
b) Wählt man $x_1=1,5$, so ergibt sich $m=2,5$.
c) Wenn man x₁ sehr dicht an 1 wählt, ist die Näherung recht genau.

Die Idee bei der Annäherung der Tangente durch Sekanten ist es, den Wert x₁ immer mehr x₀ anzunähern. Dann ergibt die Steigung der Sekanten eine immer bessere Näherung für die Tangentensteigung.

Hausaufgaben

a) Zeichnen Sie Tangenten an den Graphen der Funktion f mit $f(x)=x^2$ in Punkten A(3| 9) und B(-2| 4) und bestimmen Sie aus der Zeichnung die Steigungen dieser Geraden.
b) Bestimmen Sie wie in Aufgabe 10 Näherungswerte für die Steigungen der Tangenten an den Graphen der Funktion f mit $f(x)=x^2$ in Punkten A(3| 9) und B(-2| 4) und vergleichen Sie Ihre Ergebnisse mit den Ergebnissen aus Aufgabenteil a.
c) Bestimmen Sie wie in Aufgabe 10 einen Näherungswert für die Steigung der Tangenten an den Graphen der Funktion f mit $f(x)=3 x^2+2$ im Punkt A(2| f(2)).

a) Die Steigungen sind ungefähr 6 und -4.
b) Die Steigungen sind 6 und -4.

c) Die Steigung ist 12.

Aufgabe Differenzieren

a) Zeichnen Sie Tangenten an den Graphen der Funktion f mit $f(x)=\frac{1}{x}$ in Punkten A(1| f(1)) und B(-0,5| f(-0,5)) und bestimmen Sie aus der Zeichnung die Steigungen dieser Geraden.
b) Bestimmen Sie wie in Aufgabe 10 Näherungswerte für die Steigungen der Tangenten an den Graphen der Funktion f mit $f(x)=\frac{1}{x}$ in Punkten A(1| f(1)) und B(-0,5| f(-0,5)) und vergleichen Sie Ihre Ergebnisse mit den Ergebnissen aus Aufgabenteil a.

a) Die Steigungen sind ungefähr -1 und -4.

b) Die Steigungen sind -1 und -4.

Testen

Sie sollten nach dem Test sagen können:

Ich kann Sekanten und Tangenten an Graphen von Funktionen zeichnen und ihre Steigungen aus der Zeichnung bestimmen.
Ich kann bei gegebener Funktionsvorschrift rechnerisch Sekantensteigungen bestimmen und damit Tangentensteigungen annähern.

1a) Welchen Wert hat $\Delta x$ für die Funktion f(x)=x² im Intervall zwischen x=1 und x=3? (!1) (2) (!3) (!5) (!8) (!9)

1b) Welchen Wert hat $\Delta y$ für die Funktion f(x)=x² im Intervall zwischen x=1 und x=3? (!1) (!2) (!3) (!5) (8) (!9)

1c) Was gibt $\Delta y$ in 1b) an? (Um wie viele Einheiten sich der Funktionswert zwischen den Stellen 1 und 3 verändert.)(!Die Funktionswerte an den Stellen 1 und 3.) (!Die Stellen für die Funktionswerte 1 und 3.) (!Die durchschnittliche Veränderung des Funktionswertes zwischen den Stellen 1 und 3.)

1d) Ein Teilstück einer Achterbahn kann mit der Funktion h[x]=0,2x³+x beschrieben werden. Mit welcher Berechnung kann die Tangentensteigung an der Stelle x=2 am besten angenähert werden? ($\frac{h[2,0001]-h[2]}{2,0001-2}$) (!$\frac{2,0001-2}{h[2,0001]-h[2]}$) (!$\frac{h[2,001]-h[2]}{2,001-2}$)(!$\frac{2,001-2}{h[2,001]-h[2]}$) (!$\frac{h[2,01]-h[2]}{2,01-2}$)(!$\frac{2,01-2}{h[2,01]-h[2]}$)

Wenn Ihre Lösungsrate mindestens 75% beträgt, gehen Sie zu den weiteren Aufgaben. Wenn Sie weniger als 75% richtig haben, überprüfen Sie genau Ihre Fehler und versuchen Sie zu verstehen, was Sie falsch gemacht haben.

Der Differenzenquotient

Sie haben für diese Aufgabe 10 Minuten Zeit.

Aufgabe 11

Erläutern Sie die Vorgehensweise im Abschnitt "Von der mittleren zur momentanen Änderungsrate" und im Abschnitt "Von der Sekanten- zur Tangentensteigung". Vergleichen Sie dabei die Vorgehensweisen und arbeiten Sie Gemeinsamkeiten heraus.

Plenumsphase

Der Differentialquotient

Sie haben für diesen Abschnitt 15 Minuten Zeit.

Merke

Der Differentialquotient f'(x₀ ) ist definiert als Grenzwert eines Differenzenquotienten:

Differentialquotient $f'(x_0) = \lim_{x_1\to x_0} \frac{f(x_1)-f(x_0)}{x_1-x_0}$

Der Differentialquotient f'(x₀) wird auch als Ableitung der Funktion f an der Stelle x₀ bezeichnet.

Der Differentialquotient f'(x₀ )

• beschreibt die momentane Änderungsrate der Funktion f an der Stelle x₀ und entsteht im Rahmen eines Grenzprozesses, wenn man bei der durchschnittlichen Änderungsrate zwischen x₀ und x₁ den Wert x₁ immer mehr dem Wert x₀ annnährt,
• beschreibt die Steigung der Tangenten an den Graphen der Funktion im Punkt A(x₀|f(x₀)) und entsteht, wenn man im Rahmen eines Grenzprozesses bei der Sekantensteigung zwischen den Punkten A(x₀|f(x₀)) und B(x₁|f(x₁)) den Punkt B(x₁|f(x₁)) immer mehr dem Punkt A(x₀|f(x₀)) annähert.

Im Applet können Sie den Übergang vom Differenzenquotienten zum Differentialquotienten nachvollziehen.

Übertragen Sie die Definition des Differentialquotienten zusammen mit einer geeigneten Skizze in Ihr Heft.

Aufgabe 12

Verschieben Sie im Applet den Punkt B nahe zu A und beobachten Sie den Wert des Differenzenquotienten. Was passiert, wenn B und A zusammenfallen? Beschreiben Sie Ihre Beobachtungen in Ihrem Heft.

Testen

Sie sollten nach dem Test sagen können:

Ich kann die Bedeutung von Differenzenquotienten und des Differentialquotienten erklären. Ich kann erklären, wie man mit Hilfe von Differenzenquotienten den Differentialquotienten annähern kann.

Ordnen Sie die Ausdrücke unten den richtigen Oberbegriffen zu.

Differenzenquotient	Sekantensteigung	Durchschnittsgeschwindigkeit	mittlere Änderungsrate	$\frac{f(x)-f(x_0)}{x-x_0}$	$\frac{y_2-y_1}{x_2-x_1}$
Differentialquotient	Tangentensteigung	Momentangeschwindigkeit	$\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}$	momentane Änderungsrate

Wenn Sie mehr als zwei falsche Zuordnungen gemacht haben, sollten Sie vor der Weiterarbeit noch einmal die Definitionen und Zusammenhänge der Begriffe wiederholen.

Die Ableitungsfunktion

Für diesen Abschnitt haben Sie 20 Minuten Zeit.

Man kann nun zu jedem x-Wert den Differentialquotienten f'(x) bestimmen.

Ordnet man jedem x -Wert den zugehörigen Wert der Ableitung f'(x) zu, so erhält man eine neue Funktion, die Ableitungsfunktion f' .

Sie sollten nach der Aufgaben sagen können:

Ich kann den Graphen der Ableitungsfunktion skizzieren, wenn der Graph der Funktion gegeben ist.

Aufgabe 13

a) Auf dem ausliegenden Arbeitsblatt ist der Graph der Funktion f mit f(x)=x² gegeben. Zeichnen Sie an mehreren Stellen die Tangenten an den Graphen der Funktion und bestimmen Sie deren Steigungen. Legen Sie nun eine Tabelle an, in der Sie die x-Werte und die zugehörigen Werte der Tangentensteigung eintragen. Die Werte dieser Tabellen übertragen Sie in ein neues Koordinatensystem; dies ist der Graph der Ableitungsfunktion. Stellen Sie eine Vermutung für die Funktionsvorschrift der Ableitungsfunktion auf.
b) Auf der zweiten Seite des ausliegenden Arbeitsblatt ist der Graph der Funktion f mit f(x)=x³ gegeben. Zeichnen Sie an mehreren Stellen die Tangenten an den Graphen der Funktion und bestimmen Sie deren Steigungen. Zeichnen Sie nun in einem neuen Koordinatensystem den Graphen der Ableitungsfunktion. Stellen Sie eine Vermutung für die Funktionsvorschrift der Ableitungsfunktion auf.

c) Vergleichen Sie Ihre Ergebnisse mit einer anderen Gruppe.

Hausaufgaben:

• Seite 132/1, Seite 132/3a,b (Bigalke-Köhler, Mathematik 1, Hessen, Cornelsen-Verlag 2009, ISBN 978-3-464-57449-2) bzw.
• Seite 50/1, Seite 50/3a,b (Bigalke-Köhler, Mathematik Band 1, Analysis, Cornelsen-Verlag 2007, ISBN 978-3-06-000478-2) bzw.
• Seite 52/2, 52/3 (Lambacher-Schweizer, Mathematik Leistungskurs, Klett-Verlag 2011, ISBN 978-3-12-735601-4)

Übungen für Fortgeschrittene:

• Seite 132/2 (Bigalke-Köhler, Mathematik 1, Hessen, Cornelsen-Verlag 2009, ISBN 978-3-464-57449-2) bzw.
• Seite 50/2 (Bigalke-Köhler, Mathematik Band 1, Analysis, Cornelsen-Verlag 2007, ISBN 978-3-06-000478-2) bzw.
• Seite 52/5, 52/6 (Lambacher-Schweizer, Mathematik Leistungskurs, Klett-Verlag 2011, ISBN 978-3-12-735601-4)

Die h-Schreibweise

Für diesen Abschnitt haben Sie 90 Minuten Zeit.

Da sich dadurch einige Rechungen später einfacher gestalten lassen, betrachten wir in diesem Abschnitt noch eine andere Schreibweise für den Differenzenquotienten und den Differentialquotienten.

Die h-Schreibweise des Differenzenquotienten und des Differentialquotienten

Anstatt beim Übergang vom Differenzenquotienten zum Differentialquotienten x₁ immer mehr x₀ anzunähern, kann man auch die Differenz $h=\Delta x=x_1-x_0$ klein werden lassen. Es ist dann $x_1=x_0+h$.

Aufgabe 14

a) Überlegen Sie, wo in der folgenden Zeichnung die Größen $h$, $x_0+h$, $f(x_0+h)$, $f(x_0+h)-f(x_0)$ zu finden sind.
b) Geben Sie eine Formel für die Sekantensteigung für eine Funktion f an, wenn die Sekante durch den Punkt A(x₀| f(x₀)) und den Punkt B(x₀+h| f(x₀+h)) gehen soll.
c) Welches rechnerische Problem ergibt sich, wenn man in dieser Formel einfach h= 0 setzen würde.

Vollziehen Sie im Applet den Übergang von der Sekante zur Tangente nach. Wie ändert sich dabei h?

Sekantensteigung: $m=\frac{f(x_0+h)-f(x_0)}{h}$

Wenn man h= 0 setzt, würde man durch 0 dividieren, was ja nicht erlaubt ist. Daher können wir zur Bestimmung der Tangensteigung nicht einfach h gleich 0 setzen, sondern können nur einen Grenzwert betrachten, indem wir h immer kleiner werden lassen und so der 0 annähern.

Aufgabe 15

Gegeben ist wieder die Funktion f mit $f(x)=x^2$.

Berechnen Sie für $h = 0,1$ ($h= 0,01$ und $h = 0,001$) die Steigung der Sekanten für $x_0= 1$ und $x_1= 1+h$. (Sie können hierzu die Tabellenfunktion Ihres Taschenrechners verwenden; schreiben Sie dazu $h=0,1^n$ mit n gleich 0, 1, 2, 3,...)

Bestimmen Sie einen Näherungswert für die Steigung der Tangenten an die Parabel im Punkt A(1|1). Vergleichen Sie mit den Ergebnissen aus den Aufgaben 9 und 10.

Die Sekantensteigung ist $m=\frac{(1+h)^2-1^2}{h}=\frac{(1+0,1^n)^2-1}{0,1^n}$. Dies muss für verschiedene n ausgerechnet werden. (Bei der Tabellenfunktion des Taschenrechners muss statt n als Variable x gewählt werden.)

n	h	x1	Sekantensteigung m
0	1	2	3
1	0,1	1,1	2,1
2	0,01	1,01	2,01
3	0,001	1,001	2,001
4	0,0001	1,0001	2,0001
5	0,00001	1,00001	2,00001

Aufgabe 16

Ersetzen Sie in der Definition des Differentialquotienten den Wert x₁ durch x₀+h.

$f'(x_0)=\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}$

Dies nennt man die h-Schreibweise des Differentialquotienten.

Die Berechnung von Ableitungen

Mit Hilfe dieser h-Schreibweise des Differentialquotienten kann man die Ableitung f'(x₀) einer Funktion f an einer Stelle x₀ berechnen.

Aufgabe 17

Bearbeiten Sie nun folgende Aufgaben. Schreiben Sie die Rechnungen auch in Ihr Heft.

• Übung 1
• Übung 2

Beispielaufgabe

Betrachtet wird die Funktion $k(x)=0,002x^2$ (die in der Einstiegsaufgabe die Höhes des Kraters beschreibt).

• Die Ableitung an der Stelle x=100 wird wie folgt berechnet:

$f'(100)= \lim_{h\to 0} \frac{f(100+h)-f(100)}{h}$

$= \lim_{h\to 0} \frac{0,002 \cdot (100+h)^2-0,002 \cdot 100^2}{h}$

$= \lim_{h\to 0} \frac{0,002 \cdot (100^2+2 \cdot 100h+h^2-100^2)}{h}$

$= \lim_{h\to 0} \frac{0,002 \cdot (2 \cdot 100h+h^2)}{h}$

$= \lim_{h\to 0} 0,002 \cdot \left( 2 \cdot 100+h \right)=0,004 \cdot 100 = 0,4$

• Ganz analog lässt sich die Ableitung auch für eine beliebige Stelle x=x₀ bestimmen:

$f'(x_0)= \lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}$

$= \lim_{h\to 0} \frac{0,002 \cdot (x_0+h)^2-0,002 \cdot x_0^2}{h}$

$= \lim_{h\to 0} \frac{0,002 \cdot (x_0^2+2 \cdot x_0 \cdot h+h^2-x_0^2)}{h}$

$= \lim_{h\to 0} \frac{0,002 \cdot (2 \cdot x_0 \cdot h+h^2)}{h}$

$= \lim_{h\to 0} 0,002 \cdot \left( 2 \cdot x_0+h \right)=0,004 \cdot x_0$

Aufgabe 18

1. Bestimmen Sie mit Hilfe des Applets, wie weit das Fahrzeug im Barringer-Krater kommt.
2. Berechnen Sie mit Hilfe der Ableitungsfunktion aus der vorherigen Aufgabe, wie weit das Fahrzeug kommt.

Differenzieren

Bestimmen Sie wie in der Beispielaufgabe die Ableitung für die die Funktion $w(t)=0,001(t+8)^3$ (die in der Einstiegsaufgabe die Wasserhöhe in der Vase beschreibt) zum Zeitpunkt t=5s und für einen bliebigen Zeitpunkt t=t₀.

Aufgabe 19

1. Variieren Sie die Stelle x₀ im Applet und beschreiben Sie die Bedeutung der sich ergebenden Ortslinie.
2. Treffen Sie sich mit einem weiteren Lernteam und vergleichen Sie Ihre Lösungen.

Merke

Die Berechnung des Grenzwertes des Differenzenquotienten für eine bestimmte Stelle x₀ ergibt die Ableitung an dieser Stelle. Wird diese Berechnung für eine allgemeine Stelle x durchgeführt, so erhält man die Funktion f´(x), die jeder Stelle x die Ableitung an der Stelle zuordnet – die sogenannte Ableitungsfunktion.

Mithilfe der Ableitungsfunktion lässt sich die Steigung des Graphen an jeder beliebigen Stelle bzw. die Änderungsrate zu jedem beliebigen Zeitpunkt schnell berechnen.

Hausaufgabe:

Berechnen Sie die Ableitung der Funktion f mit f(x)=3x²+1 an der Stelle x=2 und an der Stelle x₀.

f'(2)=12 und f'(x₀)=6x₀

Üben und Vertiefen

Bearbeiten Sie zwei der drei Aufgaben. Die Anzahl der * gibt den Schwierigkeitsgrad der Aufgaben an.

Aufgabe 20 *

• Seite 133/4b (Bigalke-Köhler, Mathematik 1, Hessen, Cornelsen-Verlag 2009, ISBN 978-3-464-57449-2) bzw.
• Seite 51/4b (Bigalke-Köhler, Mathematik Band 1, Analysis, Cornelsen-Verlag 2007, ISBN 978-3-06-000478-2) bzw.
• Seite 48/3b (Lambacher-Schweizer, Mathematik Leistungskurs, Klett-Verlag 2011, ISBN 978-3-12-735601-4)

Aufgabe 21 **

• Seite 133/4c (Bigalke-Köhler, Mathematik 1, Hessen, Cornelsen-Verlag 2009, ISBN 978-3-464-57449-2) bzw.
• Seite 51/4c (Bigalke-Köhler, Mathematik Band 1, Analysis, Cornelsen-Verlag 2007, ISBN 978-3-06-000478-2) bzw.
• Seite 52/4 (Lambacher-Schweizer, Mathematik Leistungskurs, Klett-Verlag 2011, ISBN 978-3-12-735601-4)

Aufgabe 22 ***

• Seite 133/5a (Bigalke-Köhler, Mathematik 1, Hessen, Cornelsen-Verlag 2009, ISBN 978-3-464-57449-2) bzw.
• Seite 51/5a (Bigalke-Köhler, Mathematik Band 1, Analysis, Cornelsen-Verlag 2007, ISBN 978-3-06-000478-2) bzw.
• Seite 48/10 (Lambacher-Schweizer, Mathematik Leistungskurs, Klett-Verlag 2011, ISBN 978-3-12-735601-4)

Testen

Sie sollten nach dem Test sagen können:

Ich kann die Ableitungsfunktionen für quadratische Funktionen und kubische Funktionen mit Hilfe des Grenzprozesses des Übergangs vom Differenzenquotienten zum Differentialquotienten berechnen.

Aus technischen Gründen werden in den Aufgaben an manchen Stellen eckige Klammern verwendet statt der sonst in diesem Zusammenhang üblichen runden Klammern.

1) Ordnen Sie die Formeln richtig den Oberbegriffen zu.

Differenz der x-Werte	$\Delta x$	$x_1-x_0$	h
Differenz der Funktionswerte	$\Delta y$	$f(x_1)-f(x_0)$	$f(x_0+h)-f(x_0)$

2a) Welchen Wert hat h für die Funktion f(x)=x² im Intervall zwischen x₀=1 und x₁=1,1? (!1) (0,1) (!2) (!1,1) (!3) (!0,01) (!2,1)

2b) Welchen Wert hat $f(x_0+h)$ für die Funktion f(x)=x² im Intervall für x₀=2 und h=0,1? (!2) (!4) (!1) (!0,01) (4,41) (!4,1) (!2,1) (!0,1) (!4,01)

2c) Was gibt h in der Formel $m=\frac{f(x_0+h)-f(x_0)}{h}$ an? (!Um wie viele Einheiten sich der Funktionswert zwischen den Stellen x₀ und x₀+h verändert.)(!Die Differenz der Funktionswerte.) (Die Differenz der x-Werte.) (!Die Steigung.)

2d) Wir betrachten die Funktion f[x]=0,2x³+x. Mit welcher Berechnung kann die Tangentensteigung an der Stelle x=2 am besten angenähert werden? ($\frac{f[2,0001]-f[2]}{0,0001}$) (!$\frac{0,0001}{f[2,0001]-f[2]}$) (!$\frac{f[2,001]-f[2]}{0,001}$)(!$\frac{0,001}{f[2,001]-f[2]}$) (!$\frac{f[2,01]-f[2]}{0,01}$)(!$\frac{0,01}{f[2,01]-f[2]}$)

Wenn Ihre Lösungsrate mindestens 75% beträgt, gehen Sie zu den weiteren Aufgaben. Wenn Sie weniger als 75% richtig haben, überprüfen Sie genau Ihre Fehler und versuchen Sie zu verstehen, was Sie falsch gemacht haben.

Zum Abschluss

Betrachten Sie noch einmal die beiden Einstiegsaufgaben und bearbeiten Sie schriftlich folgende Fragen:

• Was waren die Problemstellungen?
• Was waren die ersten Lösungsansätze?
• Wie sieht die mathematische Lösung aus?

Testen Schätzen Sie Ihren aktuellen Lernstand anhand des ausliegenden Selbsteinschätzungsbogen ein.

Autoren: Jochen Dörr, Tobias Rolfes, Dirk Schmerenbeck, Roland Weber<metakeywords>ZUM2Edutags,ZUM-Wiki,Mathematik-digital/Einführung in die Differentialrechnung,Mathematik-digital,Einführung in die Differentialrechnung,Mathematik,Einführung,Differentialrechnung,Lernpfad</metakeywords>