Eigenschaften ganzrationaler Funktionen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 197: | Zeile 197: | ||
{{!}} style="padding:5px" {{!}} [[Bild:A2.h.png]] | {{!}} style="padding:5px" {{!}} [[Bild:A2.h.png]] | ||
{{!}}- | {{!}}- | ||
{{!}} <strong>y = 3x<sup>5</sup>-2x<sup>2</sup>-1 </strong> {{!}}{{!}} <strong>y = = | {{!}} <strong>y = 3x<sup>5</sup>-2x<sup>2</sup>-1 </strong> {{!}}{{!}} <strong>y =2x<sup>4</sup></strong> {{!}}{{!}} <strong>y = -4x<sup>4</sup>+3x+1</strong> {{!}}{{!}} <strong>y = -2,1x<sup>9</sup>-2x<sup>8</sup>+x<sup>7</sup>-4x<sup>6</sup>+3,5x<sup>4</sup>+2,8</strong> {{!}}{{!}} <strong>y = [x<sup>2</sup>+3x+2][2x-3x<sup>3</sup>] </strong> {{!}}{{!}} <strong>y =[-3x<sup>2</sup>]<sup>3</sup>+4 </strong> {{!}}{{!}} <strong>y =7.1x<sup>5</sup>+2x<sup>3</sup>+4 </strong> {{!}}{{!}} <strong>y =[2x<sup>2</sup>-3x+1]<sup>3</sup></strong> | ||
{{!}}} | {{!}}} | ||
</div> | </div> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Version vom 12. November 2018, 15:12 Uhr
Willkommen beim Lernpfad zu den Eigenschaften ganzrationaler Funktionen
Zur Zeit beschäftigen wir uns mit ganzrationalen Funktionen, wobei du die einfachste Form, die Potenzfunktionen, bereits kennengelernt hast. Von Interesse ist hier vor allem der Verlauf einer Funktion in Abhängigkeit des Funktionsterms für betragsmäßig große x-Werte, d.h. am "linken und am rechten Rand" des Definitionsbereiches. Dieses hast du bei den Potenzfunktionen mit natürlichem Exponenten bereits kennengelernt. Im folgenden sollen die bereits bekannten Informationen über die Potenzfunktionen auf allgemeine ganzrationale Funktionen übertragen werden.
Voraussetzungen
- Du kannst den Verlauf des Funktionsgraphen einer Potenzfunktion anhand des Funktionsterms beschreiben und skizzieren.
- Du kannst den Funktionsterm einer Potenzfunktion mit Hilfe eines Gleichungssystems ermitteln.
Ziele
- Du erkennst, wann eine ganzrationale Funktion vorliegt, und wann nicht.
- Du kannst den Verlauf für betragsmäßig große x-Werte des Funktionsgraphen einer ganzrationalen Funktion anhand des Funktionsterms beschreiben.
(Z.B. "von links unten nach rechts oben") - Du kannst den Funktionsterm einer ganzrationalen Funktion mit Hilfe eines Gleichungssystems ermitteln.
Hinweise zur Bearbeitung
1. Hefteintrag
Den groben Hefteintrag hast du bereits bekommen. Ansonsten kannst du ihn dir hier herunterladen.
Fülle die noch leeren Felder mit den im Lernpfad gewonnenen Informationen aus.
2. Bearbeitung
- Bearbeite die Aufgaben mit einem Mitschüler.
- Bearbeite die Aufgaben der Reihe nach.
- Überprüfe dein Wissen am Ende jedes Abschnittes durch die Beispielaufgaben
- Nutze die versteckten Hinweise erst, wenn du mit deinem Mitschüler sicher nicht mehr weiter kommst. Versuche so lange wie möglich ohne die Hinweise auszukommen.
Wichtige Definitionen
Terme, die aus einer Summe von Potenzen (mit Exponenten aus ) bestehen, heißen Polynome.
Der höchste vorkommende Exponent entspricht dem Grad des Polynoms.
Beispiele:
2x4 - 3x3 + x - 5 ist ein Polynom vom Grad 4
-3x12 + 14x2 - 20 ist ein Polynom vom Grad 12Funktionen, deren Funktionsterme f(x) Polynome sind, nennt man ganzrationale Funktionen. Der Grad des Polynoms ist dann auch der Grad der Funktion.
Beispiel:
ist eine ganzrationale Funktion vom Grad 7Der allgemeine Funktionsterm einer ganzrationalen Funktion vom Grad n ist
Die ak nennt man Koeffizienten (0 k n).
Beispiele:
Entscheide ob folgende Funktionen ganzrational sind. Gib gegebenenfalls den Grad und alle Koeffizienten an.
- a)
- b)
- c)
- d)
a) keine ganzrationale Funktion
b) ganzrationale Funktion vom Grad 8, , , ,
c) ganzrationale Funktion vom Grad 3, , , ,
d) keine ganzrationale Funktion
Verhalten ganzrationaler Funktionen für betragsmäßig große x-Werte
Gerader Funktionsgrad
Gegeben sind die Funktionen und
- a) Zeichne die Graphen der Funktionen mit GeoGebra in ein gemeinsames Koordinatensystem.
- b) Welcher Unterschied bzw. welche Gemeinsamkeit fällt dir bezüglich des Verhaltens für betragsmäßig große x-Werte auf?
- c) Welcher Summand im Funktionsterm ist vermutlich ausschlaggebend für das Verhalten?
Verändere die Koeffizienten der Funktion 4ten Grades mit Hilfe der Schieberegler und finde heraus, welcher Summand das Verhalten des Graphen für große x-Werte beeinflusst.

- d) Welche Fälle müssen beim Koeffizienten dieses Summanden unterschieden werden? Wie wirken sich diese auf das Verhalten aus?
- e) Zeichne weitere ganzrationale Funktionen mit geradem Funktionsgrad und verschiedenen Koeffizienten in das Koordinatensystem und überprüfe damit deine Vermutungen.
- f) Fasse deine Ergebnisse zusammen und ergänze den Hefteintrag an den entsprechenden Stellen.
Ungerader Funktionsgrad
Gegeben sind die Funktionen und
- a) Untersuche die beiden Funktionen wie im vorherigen Abschnitt zum geraden Funktionsgrad.
Verändere die Koeffizienten der Funktion 3ten Grades mit Hilfe der Schieberegler und finde heraus, welcher Summand das Verhalten des Graphen für große x-Werte beeinflusst.

- b) Fasse deine Ergebnisse zusammen und ergänze den Hefteintrag an den entsprechenden Stellen.
WICHTIG
Weitere Aussagen, z.B. über die Wertemenge, Extremwerte, Symmetrie, etc., sind hier noch nicht möglich!
Vergleiche deine Ergebnisse mit dem Schulbuch (S.112)
Ein ausgefülltes Arbeitsblatt findest du hier.
Übungsaufgaben
Gib den charakteristischen Verlauf folgender Funktionen an:
- a) links oben nach rechts oben
- b) links oben nach rechts unten
- c) links oben nach rechts oben
- d) links unten nach rechts oben
- e) links unten nach rechts unten
- f) links unten nach rechts unten
- g) links oben nach rechts oben
- h) links oben nach rechts unten
- i) links unten nach rechts unten
- j) links oben nach rechts oben
- Beachte nur die Potenz mit dem höchsten Exponenten.
- Beachte die Potenzgesetze.
- Wird ein ganzes Polynom vom Grad n mit der Zahl m potenziert, so ergibt die höchste Potenz im Ergebnis. Der Rest ist nicht von Interesse!
Z.B. 4. Werden zwei Polynome vom Grad n und m und den Koeffizienten ak bzw. bj miteinander multipliziert, so ergibt das Produkt der Potenzen mit dem jeweils höchsten Exponenten, , im Ergebnis die Potenz mit dem höchsten Exponent. Z.B.
5. Achte auf die Vor- und Rechenzeichen.
Rationale Funktionen
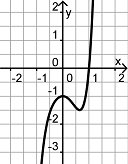
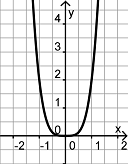
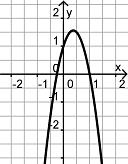
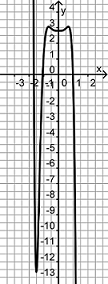
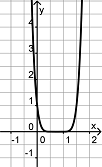
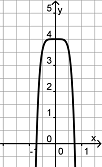
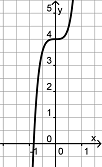
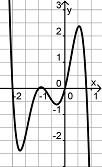
Finde die Paare aus je einem Funktionsgraph und dem dazu passenden Funktionsterm.
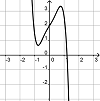 |
f(x)= -3x5 + 2x3 + 1,6x + 2 |
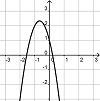 |
g(x) = -3x2 - 4x + 1 |
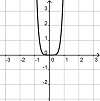 |
h(x) = (2x2)3 - 1,6x5 |
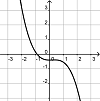 |
i(x) = (-0,7 x)3 + 0,2x2 - 0,4 |
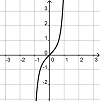 |
j(x) = 3x7 + x3 + x |
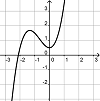 |
k(x) = x (x2 + 2x) + 0,5 |
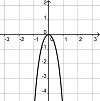 |
l(x) = -(2x4 + 3,4x2) |
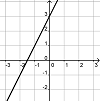 |
m(x) = 2x + 3 |
Bestimmung von Funktionstermen
Der y-Achsenabschnitt
Als y-Achsenabschnitt wird der y-Wert des Schnittpunkts mit der y-Achse genannt. Er ergibt sich, wenn für den x-Wert 0 eingesetzt wird.
Damit folgt aus der allgemeinen Funktionsgleichung
Ist der Schnittpunkt Sy mit der y-Achse gegeben, so lässt sich a0 direkt angeben.
Aufstellen eines linearen Gleichungssystems
- Die Anzahl der unbekannten Koeffizienten gibt an, wieviele Bedingungen (z.B. Punkte, die auf dem Graphen der Funktion liegen) bekannt sein müssen, um den Funktionsterm eindeutig bestimmen zu können.
- Gib immer zunächst den allgemeinen Funktionsterm an um dir einen Überblick über die gesuchten Koeffizienten zu verschaffen.
- Durch das Aufstellen von Gleichungen, mit Hilfe der Bedingungen, ergibt sich ein lineares Gleichungssystem, mit welchem sich die gesuchten Koeffizienten nach und nach bestimmen lassen.
Bestimme den Funktionsterm einer ganzrationalen Funktion mit Hilfe der jeweiligen Bedingungen:
a) Der Graph der Funktion f vom Grad 4 verläuft durch die Punkte P(-2/6), und Q(1/-1,2) als auch durch den Ursprung. Der Funktionsterm besteht nur aus Potenzen mit geradzahligem Exponenten.
b) Die Punkte P(-1/3), Q(1/0) und S(2/4,5) liegen auf dem Funktionsgraph einer Funktion dritten Grades. Der Graph schneidet die y-Achse im Punkt Sy(0/1,5)
a) Allgemeiner Funktionsterm:
(0/0)
P, Q
1.
2.
Lösen des Gleichungssystems liefert: