Einführung in die Integralrechnung: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Karl Kirst K (Mathematik/Lernpfad/Einführung in die Integralrechnung wurde nach Pentagramm/Einführung in die Integralrechnung verschoben: Unterseite) |
Main>Karl Kirst K (-kat; linkfix) |
||
| Zeile 1: | Zeile 1: | ||
---- | ---- | ||
{{Babel-1| | {{Babel-1|M-digital}} | ||
__NOTOC__ | __NOTOC__ | ||
In diesem Lernpfad können die Schüler die grundlegenden Zusammenhänge der Integralrechnung anhand vieler interaktiver Übungen entdecken. Einige Übungen sind dem gleichnamigen Lernpfad [http://www.geogebra.at/medienvielfalt/materialien/int_einfuehrung/lernpfad/index.htm Einführung in die Integralrechnung] der österreichischen Arbeitsgruppe Medienvielfalt entnommen, die aus einer Kooperation von [http://www.mathe-online.at/ mathe-online] und [http://www.geogebra.at GeoGebra] entstanden ist. | In diesem Lernpfad können die Schüler die grundlegenden Zusammenhänge der Integralrechnung anhand vieler interaktiver Übungen entdecken. Einige Übungen sind dem gleichnamigen Lernpfad [http://www.geogebra.at/medienvielfalt/materialien/int_einfuehrung/lernpfad/index.htm Einführung in die Integralrechnung] der österreichischen Arbeitsgruppe Medienvielfalt entnommen, die aus einer Kooperation von [http://www.mathe-online.at/ mathe-online] und [http://www.geogebra.at GeoGebra] entstanden ist. | ||
| Zeile 39: | Zeile 39: | ||
Maria Eirich und Andrea Schellmann, 14.09.2006 | Maria Eirich und Andrea Schellmann, 14.09.2006 | ||
Version vom 29. Januar 2007, 22:25 Uhr
In diesem Lernpfad können die Schüler die grundlegenden Zusammenhänge der Integralrechnung anhand vieler interaktiver Übungen entdecken. Einige Übungen sind dem gleichnamigen Lernpfad Einführung in die Integralrechnung der österreichischen Arbeitsgruppe Medienvielfalt entnommen, die aus einer Kooperation von mathe-online und GeoGebra entstanden ist.
1. Das Flächenproblem
- Wie groß ist der Flächeninhalt des Grundstücks?
- Wie groß ist der Wasserverbrauch?
2. Unter- und Obersumme
- Begriffsklärung Unter- und Obersumme
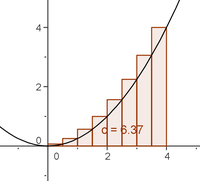
- Aufgabe: Gegeben ist die Funktion f(x) = 0.25 x².
- Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft.
- Berechne die zugehörige Ober- und Untersumme.
- Gib auch das arithmetische Mittel von Ober- und Untersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an.
- Lösung
- Zusammmenfassung im Arbeitsblatt 1
- Aufgaben zur Berechnung bestimmter Integrale
- Berechnung von Unter- und Obersummen mit GeoGebra
- Aufgaben zur Flächenberechnung mit Geogebra
3. Negative Fläche?
- Kläre die Bedeutung "negativer Flächeninhalt" (s. Arbeitsblatt 3)
- Erkläre den Unterschied zwischen dem Wert des bestimmten Integrals und dem Flächeninhalt zwischen Graph und x-Achse!
4. Integralfunktion
- Bearbeite die Punkte 1 bis 6 des dynamischen Arbeitsblatts zur Integralfunktion. Halte die Ergebnisse in deinem Heft fest.
- Überlege: Welche Funktionen der Kurvenschar sind keine Integralfunktionen?
- Bearbeite nun als Zusammmenfassung das Arbeitsblatt 4.
5. Aufgaben
6. Hauptsatz der Integralrechnung
Maria Eirich und Andrea Schellmann, 14.09.2006