Einführung in die Integralrechnung: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Main>Karl Kirst (+Babel; +kat) |
Main>A.Burgermeister |
||
| Zeile 13: | Zeile 13: | ||
**Gib auch das arithmetische Mittel von Ober- und Untersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an. | **Gib auch das arithmetische Mittel von Ober- und Untersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an. | ||
**[[Diskussion:Einführung in die Integralrechnung|Lösung]] | **[[Diskussion:Einführung in die Integralrechnung|Lösung]] | ||
*Zusammmenfassung im | *Zusammmenfassung im {{pdf|Infini_AB1.pdf}} Arbeitsblatt 1 | ||
* | *{{pdf|Infini_AB2.pdf}} Aufgaben zur Berechnung bestimmter Integrale | ||
*Berechnung von Unter- und Obersummen mit [http://www.geogebra.at/medienvielfalt/materialien/int_einfuehrung/lernpfad/content/unterobersumme_geogebra.htm GeoGebra] | *Berechnung von Unter- und Obersummen mit [http://www.geogebra.at/medienvielfalt/materialien/int_einfuehrung/lernpfad/content/unterobersumme_geogebra.htm GeoGebra] | ||
*[http://www.geogebra.at/medienvielfalt/materialien/int_einfuehrung/lernpfad/content/bestInt_ue1.htm Aufgaben zur Flächenberechnung] mit Geogebra | *[http://www.geogebra.at/medienvielfalt/materialien/int_einfuehrung/lernpfad/content/bestInt_ue1.htm Aufgaben zur Flächenberechnung] mit Geogebra | ||
Version vom 26. Januar 2007, 17:17 Uhr
1. Das Flächenproblem
- Wie groß ist der Flächeninhalt des Grundstücks?
- Wie groß ist der Wasserverbrauch?
2. Unter- und Obersumme
- Begriffsklärung Unter- und Obersumme
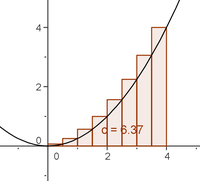
- Aufgabe: Gegeben ist die Funktion f(x) = 0.25 x².
- Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft.
- Berechne die zugehörige Ober- und Untersumme.
- Gib auch das arithmetische Mittel von Ober- und Untersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an.
- Lösung
- Zusammmenfassung im
1 Arbeitsblatt 1 - 1 Aufgaben zur Berechnung bestimmter Integrale
- Berechnung von Unter- und Obersummen mit GeoGebra
- Aufgaben zur Flächenberechnung mit Geogebra
3. Negative Fläche?
- Kläre die Bedeutung "negativer Flächeninhalt" (s. Arbeitsblatt 3)
- Erkläre den Unterschied zwischen dem Wert des bestimmten Integrals und dem Flächeninhalt zwischen Graph und x-Achse!
4. Integralfunktion
- Bearbeite die Punkte 1 bis 6 des dynamischen Arbeitsblatts zur Integralfunktion. Halte die Ergebnisse in deinem Heft fest.
- Überlege: Welche Funktionen der Kurvenschar sind keine Integralfunktionen?
- Bearbeite nun als Zusammmenfassung das Arbeitsblatt 4.
5. Aufgaben
6. Hauptsatz der Integralrechnung
Maria Eirich und Andrea Schellmann, 14.09.2006
