Einführung in quadratische Funktionen/Übungen 2: Unterschied zwischen den Versionen

Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung
K (Textersetzung - „\{\{Weiter\|([^|]+?)\|([^|]+?)\}\}“ durch „{{Fortsetzung|weiter=$2|weiterlink=$1}}“)
Zeile 73: Zeile 73:
'''Als nächstes lernst du die allgemeine quadratische Funktion kennen.'''
'''Als nächstes lernst du die allgemeine quadratische Funktion kennen.'''


{{Weiter|../allgemeine Form|Allgemeine quadratische Form}}
{{Fortsetzung|weiter=Allgemeine quadratische Form|weiterlink=../allgemeine Form}}

Version vom 2. November 2018, 21:13 Uhr

Vorlage:Quadratische Funktionen


1. Anhalteweg

Die Funktion s(v) = 0,1v2 + 1,5v ist ein Beispiel für eine Funktion, die den Zusammenhang zwischen der anfänglichen Geschwindigkeit eines Fahrzeuges in m/s und dem Anhalteweg für einen konkreten Bremsvorgang angibt.

  1. Welchen Wert hat in diesem Beispiel die Reaktionszeit tR?
  2. Welchen Wert hat die Bremsbeschleunigung aB?
  3. Wie lang ist der Anhalteweg bei einer anfänglichen Geschwindigkeit von 72 km/h (also 20 m/s)?
  4. Wie könnte der Anhalteweg verringert werden?
  1. 1,5v steht für den Reaktionsweg, d.h. tR = 1,5 s
  2. <=> <=> 2aB = 10 <=> aB = 5 (m/s2)
  3. s(20) = 0,1·202 + 1,5·20 = 40 + 30 = 70 (m)
  4. Bremsbeschleunigung erhöhen (besserer Fahrbahnbelag, gute Reifen), Reaktionszeit verringern (erhöhte Aufmerksamkeit, Bremsentechnik), Geschwindigkeit reduzieren


2. Bestimme a und b

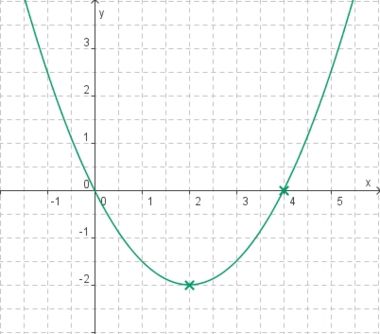
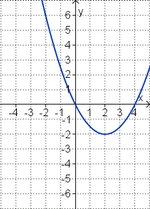
Die Parabel hat die Funktionsgleichung f(x) = ax2 + bx. Finde heraus, welche Werte a und b besitzen und erkläre wie du vorgegangen bist.

Lies die Koordinaten zweier Punkte aus dem Graphen ab und setze sie in die Funktionsgleichung ein.

Die Punkte (4/0) und (2/-2) liegen auf der Parabel, es gilt also

  • 0 = a·42 + b·4 --> b = - 4a
  • - 2 = a·22 + b·2 --> b = -1 - 2a
daraus folgt -4a = -1 -2a --> a = 0,5 und b = - 2

Üb2 Parabel 7.jpg


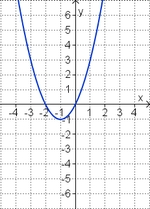
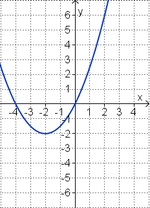
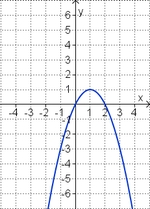
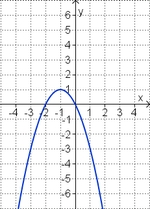
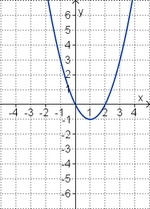
3. Term und Graph zuordnen

Ordne den Funktionsgraphen den richtigen Term zu.

Üb2 Parabel1.jpg Üb2 Parabel6.jpg Üb2 Parabel3.jpg Üb2 Parabel5.jpg Üb2 Parabel4.jpg Üb2 Parabel2.jpg
x2 + 2x 0,5x2 + 2x -x2 + 2x 0,5x2 - 2x -x2 - 2x x2 - 2x


4. Kreuze jeweils alle richtigen Aussagen an.

f(x) = 2x2 - 4x (!Die Parabel ist nach unten geöffnet.) (Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [-1|6] liegt auf dem Graphen.) (!Der Punkt [-1|-2] liegt auf dem Graphen.)

f(x) = - 0,25x2 + 3x (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (!Die Parabel ist enger als die Normalparabel.) (Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|5] liegt auf dem Graphen.) (!Der Punkt [2|7] liegt auf dem Graphen.)

Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der y-Achse symmetrisch zueinander sind? (!7x2 und -7x2) (7x2 - 2x und 7x2 + 2x) (!7x2 - 2x und -7x2 + 2x) (!7x2 - 2 und 7x2 + 2) (-7x2 + 2x und -7x2 - 2x) (!7x2 - 2 und 7x2 + 2x)

Als nächstes lernst du die allgemeine quadratische Funktion kennen.

Allgemeine quadratische Form
Abgerufen von „https://unterrichten.zum.de/index.php?title=Einführung_in_quadratische_Funktionen/Übungen_2&oldid=69136“