Laplace-Wahrscheinlichkeit wiederholen und vertiefen/Vorwissen: Unterschied zwischen den Versionen
Main>Matthias Scharwies K (kat geändert) |
Main>Karl Kirst K (Kasten blass -> blau) |
||
| Zeile 1: | Zeile 1: | ||
== Zufallsexperiment == | == Zufallsexperiment == | ||
{{Aufgaben | {{Aufgaben|1.1|Weißt du noch, was genau ein '''Zufallsexperiment''' ist? Schreibe es auf!}} | ||
[[Datei:Roulette.jpg|rechts|250px]] | [[Datei:Roulette.jpg|rechts|250px]] | ||
| Zeile 16: | Zeile 16: | ||
{{Aufgaben | {{Aufgaben|1.2|Welche der folgenden Beispiele sind Zufallsexperimente? <br!> Kreuze die richtigen Antworten an und klicke anschließend auf „prüfen!“}} | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| Zeile 25: | Zeile 25: | ||
{{Aufgaben | {{Aufgaben|1.3|Anna wirft mit ihrem Banknachbar Fritz eine Münze, um zu entscheiden wer morgen das Mathebuch in die Schule mitbringen muss. <br!> Lege für die beiden die oben angesprochenen ''Versuchsbedingungen'' vor dem Zufallsexperiment „Münzwurf“ fest. | ||
}} | }} | ||
| Zeile 36: | Zeile 36: | ||
In der folgenden Aufgabe, kannst du am Beispiel des Würfelwurfs kontrollieren, ob du die richtige Schreibweise beherrschst. | In der folgenden Aufgabe, kannst du am Beispiel des Würfelwurfs kontrollieren, ob du die richtige Schreibweise beherrschst. | ||
{{Aufgaben | {{Aufgaben|1.4|Orden die Begriffe, Schreibweisen und Beispiele richtig zu! <br!> Ziehe dazu die grünen Kästchen in die richtige Zeile. | ||
Fallen dir noch mehr Beipiele ein? | Fallen dir noch mehr Beipiele ein? | ||
| Zeile 64: | Zeile 64: | ||
Lösungshinweise: | Lösungshinweise: | ||
{{versteckt|{{ | {{versteckt|{{grün| | ||
*;Ergebnis: Man bezeichnet die einzelnen {{Hintergrund_gelb|Ergebnisse}} (Ausgänge) eines Zufallsexperiments mit <math>\omega_1,\omega _2,\omega _3,...,\omega_n</math>. | *;Ergebnis: Man bezeichnet die einzelnen {{Hintergrund_gelb|Ergebnisse}} (Ausgänge) eines Zufallsexperiments mit <math>\omega_1,\omega _2,\omega _3,...,\omega_n</math>. | ||
| Zeile 84: | Zeile 84: | ||
{{Aufgaben | {{Aufgaben|1.5|Bestimme für die folgenden vier Zufallsexperimente eine geeignete Ergebnismenge <math> \Omega </math>. | ||
Kreuze zur Überprüfung jeweils dessen Mächtigkeit <math>n=|\Omega|</math> an.}} | Kreuze zur Überprüfung jeweils dessen Mächtigkeit <math>n=|\Omega|</math> an.}} | ||
| Zeile 123: | Zeile 123: | ||
{{Aufgaben | {{Aufgaben|1.6|a) Notiere dir für folgende Ergebnismengen ''alle'' Ereignisse. Wie viele sind es jeweils? Kannst du ein Gesetz erkennen? | ||
:<math>\quad \Omega_1=\left\{1\right\},\qquad \Omega_2=\left\{1,2\right\},\qquad \Omega_3=\left\{1,2,3\right\},\qquad \Omega_4=\left\{1,2,3,4\right\}</math> | :<math>\quad \Omega_1=\left\{1\right\},\qquad \Omega_2=\left\{1,2\right\},\qquad \Omega_3=\left\{1,2,3\right\},\qquad \Omega_4=\left\{1,2,3,4\right\}</math> | ||
| Zeile 142: | Zeile 142: | ||
Lösung: {{Lösung_versteckt| | Lösung: {{Lösung_versteckt| | ||
:a) Das vermutete Gesetz lautet: | :a) Das vermutete Gesetz lautet: | ||
{{ | {{grün|<math>\mathrm{Zu\ jedem\ } \Omega\ \mathrm{gibt\ es\ } 2^{\left|\Omega\right|}\ \mathrm{verschiedene\ Ereignisse.} </math> | ||
}} | }} | ||
| Zeile 157: | Zeile 157: | ||
{{Aufgaben | {{Aufgaben|1.7|Schreibe auf, was man unter den Begriffen '''Laplace-Experiment''', '''Laplace-Würfel''' und '''Laplace-Wahrscheinlichkeit''' versteht!}} | ||
{{Lösung versteckt|{{Kasten_grün| | {{Lösung versteckt|{{Kasten_grün| | ||
| Zeile 176: | Zeile 176: | ||
{{ | {{blau|'''„Racing Game with One Die“ (Rennspiel mit einem Würfel)''' | ||
---- | ---- | ||
| Zeile 201: | Zeile 201: | ||
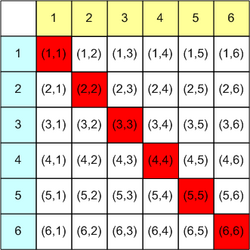
{{Aufgaben | {{Aufgaben|1.8|[[Datei:Pasch.jpg|right]]Anna würfelt mit zwei unterscheidbaren Würfeln. | ||
Wie groß ist die Wahrscheinlichkeit, dass sie einen Pasch würfelt?}} | Wie groß ist die Wahrscheinlichkeit, dass sie einen Pasch würfelt?}} | ||
Version vom 14. Mai 2018, 10:03 Uhr
Zufallsexperiment
Versuche dich zu erinnern und schreibe eine möglichst genaue Beschreibung des Begriffs "Zufallsexperiment" auf. Informiere dich wenn nötig in deinen Unterlagen aus der Schule oder recherchiere im Internet danach.
(Ziehung der Lottozahlen) (Schere, Stein, Papier) (!Wettervorhersage) (!Elfmeterschießen im WM-Finale) (dreimaliges Werfen eines Würfels) (ein Marmeladenbrot fällt vom Tisch) (!Benotung deiner Klassenarbeit) (Werfen einer Münze) (Werfen eines gezinkten Würfels) (!Geschwindigkeitsmessung der Polizei) (!physikalisches Experiment)
Hinweis: Du kannst das Multiplechoice-Quiz nochmal versuchen, indem du nach Aufgabe 1.5 die Buttons „Korrektur“ und „Neustart“ anklickst!
Anna wirft mit ihrem Banknachbar Fritz eine Münze, um zu entscheiden wer morgen das Mathebuch in die Schule mitbringen muss. <br!> Lege für die beiden die oben angesprochenen Versuchsbedingungen vor dem Zufallsexperiment „Münzwurf“ fest.
Durch Markieren der grauen Fläche wird ein Lösungsvorschlag sichtbar: Es wird festgelegt, dass die Münze auf den gebeugten Zeigefinger gelegt und mit dem Daumen in die Luft geschnipst werden soll. Die Münze wird gefangen und auf den Handrücken gelegt. Die Seite gewinnt, welche nach der Landung oben liegt.
Ergebnis und Ereignis
Zur korrekten mathematischen Beschreibung von Zufallsexperimenten benötigt man eine formale Sprache.
In der folgenden Aufgabe, kannst du am Beispiel des Würfelwurfs kontrollieren, ob du die richtige Schreibweise beherrschst.
Orden die Begriffe, Schreibweisen und Beispiele richtig zu! <br!> Ziehe dazu die grünen Kästchen in die richtige Zeile.
Fallen dir noch mehr Beipiele ein?
(Sollte dieses Quiz auf deinem Computer nicht funktionieren, musst du unter deinen ZUM-Wiki Einstellungen PNG statt HTML als Anzeigeformat von TeX-Umgebungen einstellen!)
| Ergebnis | 6 | |
| Ereignis | ||
| Elementarereignis | ||
| Ergebnismenge | ||
| Gegenereignis | ||
| unmögliches Ereignis | ||
| Mächtigkeit des Ergebnisraums |
Lösungshinweise:
Vorlage:Versteckt
Bestimme für die folgenden vier Zufallsexperimente eine geeignete Ergebnismenge .
Kreuze zur Überprüfung jeweils dessen Mächtigkeit an.
Lösungshinweise:
Vorlage:Versteckt
a) Notiere dir für folgende Ergebnismengen alle Ereignisse. Wie viele sind es jeweils? Kannst du ein Gesetz erkennen?
b) Wie viele Ereignisse gibt es bei dem Zufallsexperiment „Werfen von drei Münzen“?
Lösungshinweise:
Vorlage:Versteckt
Lösung:
Laplace-Wahrscheinlichkeit
Pierre-Simon Laplace![]() (1749 - 1827) war ein Physiker und Mathematiker, unter anderem auch am Hofe Napoleons.
<br!> Er beschäftigte sich mit der Wahrscheinlichkeitsrechnung, vor allem in Verbindung mit dem Glücksspiel.
(1749 - 1827) war ein Physiker und Mathematiker, unter anderem auch am Hofe Napoleons.
<br!> Er beschäftigte sich mit der Wahrscheinlichkeitsrechnung, vor allem in Verbindung mit dem Glücksspiel.
„Racing Game with One Die“ (Rennspiel mit einem Würfel)
- Hast du Lust auf eine kurzes Laplace-Experiment zu zweit, oder gegen den Computer?
Vorlage:Rechtsklick FensterRacing Game with One Die ist ein Autorennspiel auf einer englischsprachigen Internetseite (dazu muss Java installiert sein).
- Mit Hilfe des einfachen Würfelwurfs wird entschieden, welches Auto nach vorne fahren darf.
Anleitung:
- Öffne den Link in einem neuen Fenster.
- Entscheidet euch im mittleren Kasten, wer von euch das rote oder das blaue Auto „fährt“.
- Klickt nun im oberen Kasten so oft auf den Buton „Roll Die“, bis ein Auto über die Ziellinie fährt!
Es ist voreingestellt, dass rot bei ungerader Augenzahl fährt („Red moves on“) und blau bei gerader Augenzahl weiterkommt. - Wenn ihr auf den Button „Restart“ klickt, kann es von vorne los gehen.
- Verändere die Einstellungen nach deinen Wünschen:
- Mit dem Schieberegler „Race segments“ stellt ihr die Länge der Rennbahn, also die Anzahl der Spiele ein.
- Jetzt müsst ihr noch untereinander aushandeln, bei welchen Augenzahlen euer Auto fahren darf.
- Im unteren Kasten könnt ihr viele Rennen auf einmal durchführen lassen.
- Auf die Plätze, fertig, los!
Lösungshilfe: Vorlage:Versteckt
- Man kann aus der Tabelle prima die Ergebnismenge und das Ereignis „Pasch“ ablesen:
- Man sagt dazu „36-Feldertafel“, auf Grund der Mächtigkeit der Ergebnismenge.