Winkelhalbierende, Mittelsenkrechte, Lot: Unterschied zwischen den Versionen
Main>Petra Bader Keine Bearbeitungszusammenfassung |
Main>Petra Bader Keine Bearbeitungszusammenfassung |
||
| Zeile 18: | Zeile 18: | ||
}} | }} | ||
<br> | <br> | ||
= Das Lot = | = Das Lot = | ||
Version vom 25. Februar 2007, 15:53 Uhr
Lernpfade: Winkelhalbierende, Mittelsenkrechte und Lot
Die nachfolgende Unterrichtssequenz besteht aus drei Lernpfaden zu den Themen Winkelhalbierende, Mittelsenkrechte und Lot. Notwendige Schülermaterialien werden am Anfang des jeweiligen Lernpfades angegeben bzw. zum Download zur Verfügung gestellt.
 |
Beachte: |
1. Streich: Die Winkelhalbierende
Materialien: 1. 
Arbeitsblatt zur Winkelhalbierenden und 2. 
orange-farbenes gleichschenkliges Dreieck (Tonpapier)
2. Streich: Die Mittelsenkrechte
Material: Arbeitsblatt zur Mittelsenkrechten
3. Streich: Das Lot
Material: Arbeitsblatt zum Lot
Das Lot
Das Lot errichten
|
Auf einem ganz bestimmten Punkt |  |
Wie wird der Ort, an dem der Tannenbaum aufgestellt werden soll, beschrieben?
Aufgabe:
- Nimm ein Blatt Papier zur Hand und zeichne eine 6cm-lange Strecke [AB]!
- Wähle einen beliebigen Punkt P auf der Strecke, der die Strecke nicht halbiert!
- Überlege: Wie konstruiert man eine senkrechte Gerade, die durch den Punkt P verläuft? Diese senkrechte Gerade wird auch als Lot bezeichnet! Überprüfe Deine Konstruktionsschritte anhand der linken Skizzen!
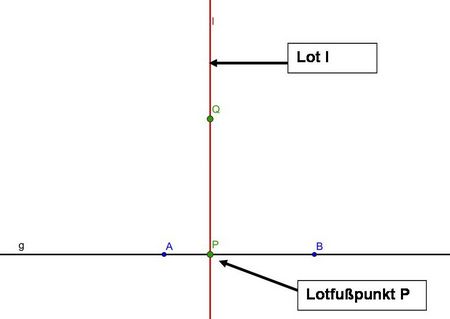
Definition des Lotes:
Eine Senkrechte durch einen Punkt Q zu einer Geraden g nennt man Lot.
Der Schnittpunkt des Lotes l mit g heißt Lotfußpunkt P.
Konstruktion: Errichten eines Lotes auf einer Geraden g im Punkt P
Überlege Dir die einzelnen Konstruktionsschritte um ein Lot im Punkt P auf einer Geraden g zu errichten!
Überprüfe Deine Überlegungen mit Deinem/r NachbarIn!
Merke:
Gilt P ∈ g, so sagt man auch: Im Punkt P wird das Lot zu g errichtet.
Arbeitsaufträge:
- Übertrage die Definition und die Merkregel vom Lot auf Dein Arbeitsblatt!
- Konstruiere auf dem Arbeitsblatt im Punkt P auf der Geraden g das Lot l! Beschrifte Deine Zeichnung (Lot, Lotfußpunkt etc.)!
- Übertrage, die (korrigierten) Konstruktionsschritte auf Dein Arbeitsblatt!
- Welche weiteren Beispiele für ein Lot aus Deinem Alltag kennst Du?
Das Lot fällen
 | Durch den Schornstein mit Vergnügen Sehen sie die Hühner liegen, Max und Moritz auf dem Dache Schnupdiwup! Da wird nach oben |
Welchen "Weg" muss die Angelschnur nehmen, damit Max und Moritz die Hähnchen erangeln können?
Konstruktion: Fällen eines Lotes vom Punkt P auf eine Gerade g
Überlege Dir die einzelnen Konstruktionsschritte um ein Lot von einem Punkt P auf eine Geraden g zu fällen!
Überprüfe Deine Überlegungen mit Deinem/r NachbarIn!
Überprüfe Deine Konstruktionsschritte anhand der rechten Skizzen!
Merke:
Gilt P ∉ g, so sagt man auch: Im Punkt P wird das Lot auf g gefällt.
Arbeitsaufträge:
- Konstruiere auf dem Arbeitsblatt vom Punkt P das Lot l auf die Geraden g! Beschrifte Deine Zeichnung (Lot, Lotfußpunkt etc.)!
- Übertrage, die (korrigierten) Konstruktionsschritte auf Dein Arbeitsblatt!
- Welche weiteren Beispiele für ein Lot aus Deinem Alltag kennst Du?
Konstruieren mit GeoGebra:
- Speichere folgende
Datei in Deinem Ordner ab! - Fälle das Lot vom Punkt P auf die Gerade g! Orientiere Dich dabei an den Konstruktionsschritten auf dem Arbeitsblatt!
- Speichere die erstellte Konstruktion unter "Lotfaellen_<<DeinName_Haus>>" im Klassenverzeichnis ab!
Rätsel zum Lot
Vertiefung und Wiederholung
Hausaufgabe: S. 18 Nr 6 Welches Buch? Titel
Petra Bader 26. Oktober 2006 (METDST)
