Figuren im Koordinatensystem: Unterschied zwischen den Versionen
Main>Karl Kirst K (linkfix) |
Main>Karl Kirst (Wiederherstellung der gewünschten Version) |
||
| Zeile 29: | Zeile 29: | ||
<ggb_applet height="360" width="560" showResetIcon="true" filename="Koordinatensystempunkt.ggb" /><br /><br /> | <ggb_applet height="360" width="560" showResetIcon="true" filename="Koordinatensystempunkt.ggb" /><br /><br /> | ||
{{ | {{Merken| | ||
MERK= | |||
Punkte im Koordinatensystem kann man durch zwei '''Zahlen''' (die wir dann '''Koordinaten''' nennen) beschreiben. Wichtig ist dabei der "Null-Punkt" (der '''Ursprung''') des Koordinatensystems. Damit ist derjenige Punkt gemeint, an dem sich die beiden Achsen schneiden. | Punkte im Koordinatensystem kann man durch zwei '''Zahlen''' (die wir dann '''Koordinaten''' nennen) beschreiben. Wichtig ist dabei der "Null-Punkt" (der '''Ursprung''') des Koordinatensystems. Damit ist derjenige Punkt gemeint, an dem sich die beiden Achsen schneiden. | ||
Wollen wir nun z.B. einen Punkt mit der ersten Koordinate 7 (die erste Koordinate nennen wir '''x-Koordinate''') und der zweiten Koordinate 3 (diese heißt '''y-Koordinate''') in das Koordinatensystem eintragen, so gehen wir vom Ursprung aus erst 7 Einheiten nach rechts und dann 3 Einheiten nach oben. Wir schreiben dann P(7/3). | Wollen wir nun z.B. einen Punkt mit der ersten Koordinate 7 (die erste Koordinate nennen wir '''x-Koordinate''') und der zweiten Koordinate 3 (diese heißt '''y-Koordinate''') in das Koordinatensystem eintragen, so gehen wir vom Ursprung aus erst 7 Einheiten nach rechts und dann 3 Einheiten nach oben. Wir schreiben dann P(7/3). | ||
| Zeile 48: | Zeile 49: | ||
}} | }} | ||
{{ | {{Arbeiten|NUMMER=2|ARBEIT= | ||
Verändere die Figur nun so, dass die Punkte A, B, ..., H folgende Koordinaten haben: | Verändere die Figur nun so, dass die Punkte A, B, ..., H folgende Koordinaten haben: | ||
| Zeile 58: | Zeile 59: | ||
}} | }} | ||
{{ | {{Arbeiten|NUMMER=3|ARBEIT= | ||
Trage die folgenden Punkte in ein Koordinatenystem ein und verbinde sie in alphabetischer Reihenfolge: | Trage die folgenden Punkte in ein Koordinatenystem ein und verbinde sie in alphabetischer Reihenfolge: | ||
A(3/1), B(5/1), C(7/3), D(7/10), E(6/11), F(3/11), G(2/10), H(2/8), I(3/8), J(3/7), K(2/7), L(2/6), M(1/6), N(1/5), O(2/5), P(2/4), Q(4/5), R(2/3), S(2/2), T(3/1) | A(3/1), B(5/1), C(7/3), D(7/10), E(6/11), F(3/11), G(2/10), H(2/8), I(3/8), J(3/7), K(2/7), L(2/6), M(1/6), N(1/5), O(2/5), P(2/4), Q(4/5), R(2/3), S(2/2), T(3/1) | ||
| Zeile 67: | Zeile 68: | ||
}} | }} | ||
<br /><br /> | |||
{{Autoren|Reinhard Schmidt}} | {{Autoren|Reinhard Schmidt}} | ||
Version vom 2. April 2009, 19:02 Uhr
| Vorlage:Lernpfad-M | Vorlage:Kurzinfo-2 |
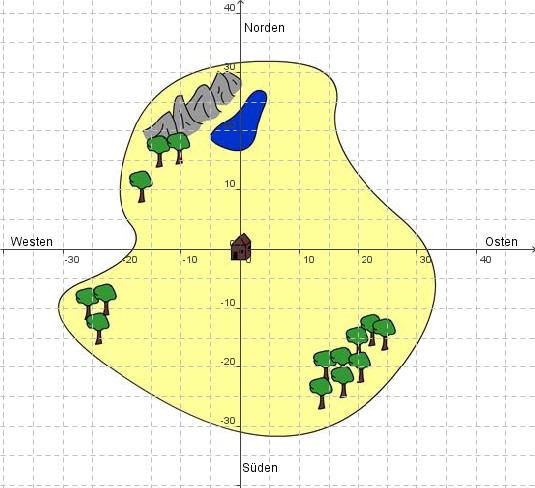
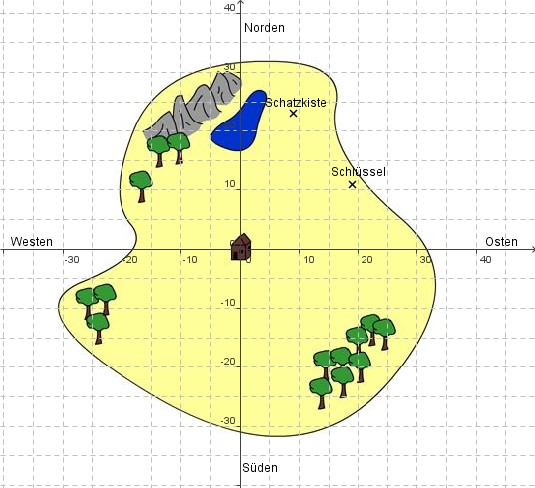
Schatzsuche
Käpt'n Flint möchte seinen alten Piratenschatz, den er vor Jahren auf der Insel Goldirum vergraben hat, zurückholen. Da er selbst zu alt für die Sache ist, gibt er seinen beiden treuesten Matrosen folgende Anweisung:
Ihr geht zunächst zur Hütte der verlassenen Geister, die sich gut sichtbar genau in der Mitte der Insel befindet. Joe, du wirst den Schlüssel der Schatzkiste suchen. Du findest ihn, wenn du von der Hütte aus zunächst 19 Meter nach Osten und dann 11 Meter nach Norden gehst. Und du, Jim, suchst die Schatztruhe. Dafür musst du erst 9 Meter nach Osten und dann 23 Meter nach Norden gehen.
Findest du den Schlüssel und die Schatztruhe?
Das Koordinatensystem
Hier siehst du ein Koordinatensystem, in das der Punkt P eingetragen wurde:
Die Datei [INVALID] wurde nicht gefunden.
Bilder im Koordinatensystem
Mit Hilfe von Koordinaten kann man Bilder beschreiben. Unten siehst du einen Fisch im Koordinatensystem (das wird noch genauer erklärt). Du kannst den Fisch zeichnen, wenn du die Koordinaten der Punkte A, B, ..., H kennst.
Die Datei [INVALID] wurde nicht gefunden.