Einführung in quadratische Funktionen/Übungen 3

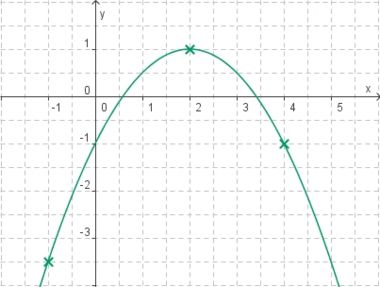
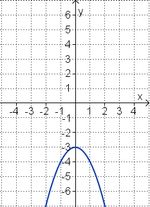
Funktionsterm finden

Die Parabel hat die Funktionsgleichung

f(x) = ax² + bx + c.

Welcher Funktionsterm passt?

(-0,5x² + 2x - 1) (!0,5x² - 2x + 3) (!-2x² + 8x - 7) (!-0,5x² + 2x + 1) (!0,5x² - 2x - 1)

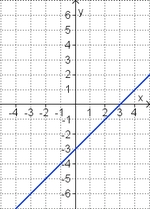
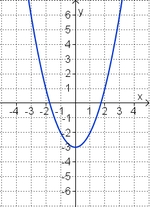
Term und Graph zuordnen

Ordne den Funktionsgraphen den richtigen Term zu.

x2 + 3	-x2 + 3	-x + 3	-x2 - 3	x - 3	x2 - 3

Kreuze jeweils alle richtigen Aussagen an

f(x) = –2x² + 3x – 4 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt [2|-6] liegt auf dem Graphen.) (Der Punkt [1|1] liegt nicht auf dem Graphen.)

Welche Terme gehören zu einer Funktion, deren Graph symmetrisch zur y-Achse ist? (7x²) (7x² - 2) (7x² + 3) (!7x² - 2x) (!7x² + 3x) (!7x² - 2x + 3)

Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der y-Achse symmetrisch zueinander sind? (!7x² und -7x²) (7x² - 2x und 7x² + 2x) (!7x² - 2x und -7x² + 2x) (!7x² - 2 und 7x² + 2) (-7x² + 2x und -7x² - 2x)

Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der x-Achse symmetrisch zueinander sind? (7x² und -7x²) (!7x² - 2x und 7x² + 2x) (!7x² - 2 und 7x² + 2) (7x² - 2 und -7x² + 2) (!7x² - 2 und -7x² + 2x)

Memo-Quiz

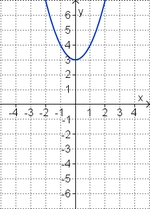
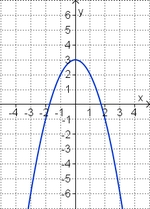
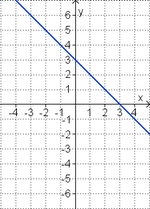
Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen).

f(x) = x2 + 3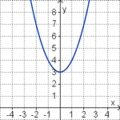
f(x) = -x2 + 3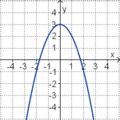
f(x) = 3x2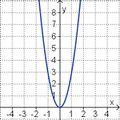
f(x) = 0,2x2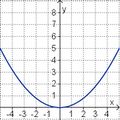
f(x) = x2 + 2x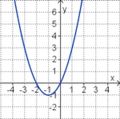
f(x) = –x2 + 2x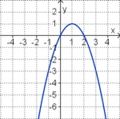
f(x) = x2 – 2x – 3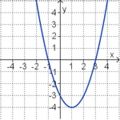
f(x) = –x2 – 2x + 3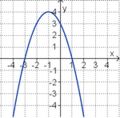

*Zusatz: Weitere interaktive Übungen

• Zeichne den Graphen
• Übung 1

Autoren: Reinhard Schmidt, Christian Schmidt, Maria Eirich, Andrea Schellmann

Weiterführende Links

• Videoanalyse: Geschwindigkeit und Bremswege von Wolfgang Riemer