Einführung in quadratische Funktionen/Übungen 3

Falls es Probleme mit der Ansicht gibt, bitte Firefox als Browser verwenden!

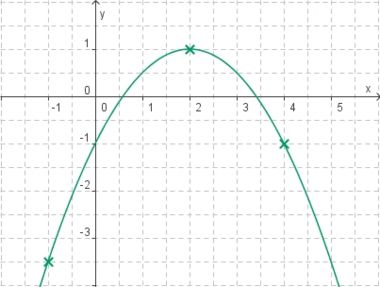
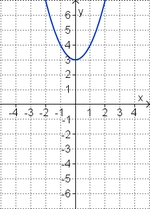
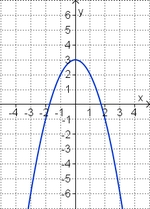
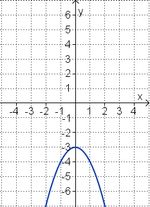
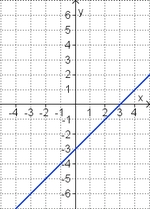
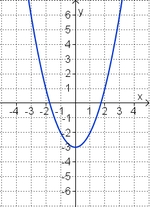
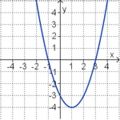
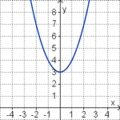
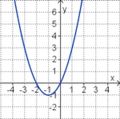
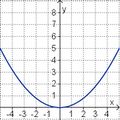
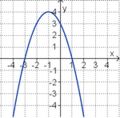
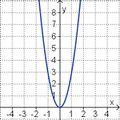
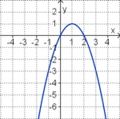
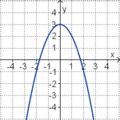
Aufgabe 1: Funktionsterm finden Die Parabel hat die Funktionsgleichung f(x) = ax2 + bx + c. Welcher Funktionsterm passt? -2x2 + 8x - 7 -0,5x2 + 2x + 1 -0,5x2 + 2x - 1 0,5x2 - 2x + 3 0,5x2 - 2x - 1 prüfen! neu starten Aufgabe 2: Term und Graph zuordnen Ordne den Funktionsgraphen den richtigen Term zu. x2 - 3x - 3x2 + 3-x2 + 3-x2 - 3-x + 3 neu starten Aufgabe 3: Multiple Choice Kreuze jeweils alle richtigen Aussagen an. <b>f Die Parabel ist enger als die Normalparabel. Der Punkt [2|-6] liegt auf dem Graphen. x Die Parabel ist nach unten geöffnet. Die Parabel ist weiter als die Normalparabel. Die Parabel ist nach oben geöffnet. Der Punkt [1|1] liegt nicht auf dem Graphen. <br> <b>Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der x-Achse symmetrisch zueinander sind?</b> 7x2 und -7x2 7x2 - 2 und -7x2 + 2x 7x2 - 2 und -7x2 + 2 7x2 - 2 und 7x2 + 2 7x2 - 2x und 7x2 + 2x <br> <b>Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der y-Achse symmetrisch zueinander sind?</b> 7x2 und -7x2 7x2 - 2 und 7x2 + 2 -7x2 + 2x und -7x2 - 2x 7x2 - 2x und -7x2 + 2x 7x2 - 2x und 7x2 + 2x <br> <b>Welche Terme gehören zu einer Funktion, deren Graph symmetrisch zur y-Achse ist?</b> 7x2 - 2x + 3 7x2 + 3 7x2 + 3x 7x2 - 2x 7x2 7x2 - 2 prüfen! neu starten Aufgabe 4: Memo-Quiz Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen). f(x) = 0,2x2 f(x) = x2 + 2x f(x) = –x2 – 2x + 3 f(x) = x2 – 2x – 3 f(x) = 3x2 f(x) = -x2 + 3 f(x) = –x2 + 2x f(x) = x2 + 3 neu starten *Zusatz: Weitere interaktive Übungen Zeichne den Graphen Übung 1 Autoren: Reinhard Schmidt, Christian Schmidt, Maria Eirich, Andrea Schellmann Weiterführende Links Videoanalyse: Geschwindigkeit und Bremswege von Wolfgang Riemer