Diagramme auswerten und interpretieren/Dreiecksdiagramm: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
main>Karl Kirst K (Karl Kirst verschob Seite Diagramme in Geographie erstellen, auswerten und interpretieren/Das Dreiecksdiagramm nach Diagramme auswerten und interpretieren/Das Dreiecksdiagramm, ohne dabei eine Weiterleitung anzulegen) |
main>Karl Kirst (Überschriften eine Hierarchie tiefer) |
||
| Zeile 2: | Zeile 2: | ||
<br><br> | <br><br> | ||
={{Schrift_grün|Einführung}}= | =={{Schrift_grün|Einführung}}== | ||
Um die Abhängigkeit von zwei Größen in einem Diagramm darzustellen benutzt man üblicherweise ein x-y-Koordinatensystem. In vielen Fällen hängen aber drei auch mehr Größen voneinander ab. Speziell für drei Größen wie z.B. <br><br> | Um die Abhängigkeit von zwei Größen in einem Diagramm darzustellen benutzt man üblicherweise ein x-y-Koordinatensystem. In vielen Fällen hängen aber drei auch mehr Größen voneinander ab. Speziell für drei Größen wie z.B. <br><br> | ||
| Zeile 22: | Zeile 22: | ||
</small><br> | </small><br> | ||
= {{Schrift_grün|Ablesen von Werten im Dreiecksdiagramm}} = | == {{Schrift_grün|Ablesen von Werten im Dreiecksdiagramm}} == | ||
<center>[[Datei:Dreicksdiagramm.png]]</center><br><br> | <center>[[Datei:Dreicksdiagramm.png]]</center><br><br> | ||
| Zeile 87: | Zeile 87: | ||
Bei der Darstellung einer zeitlichen Entwicklung kann man die Abhängikeit der drei Größen voneinander untersuchen. Ist die Kurve weitgehend (oder in Teilen) parallel zu einer der drei Seiten, so hat eine der drei Größen einen konstanten (im betrachteten Zeitraum konstanten) Anteil. Voneinander abhängig sind nur die beiden anderen Größen. }} | Bei der Darstellung einer zeitlichen Entwicklung kann man die Abhängikeit der drei Größen voneinander untersuchen. Ist die Kurve weitgehend (oder in Teilen) parallel zu einer der drei Seiten, so hat eine der drei Größen einen konstanten (im betrachteten Zeitraum konstanten) Anteil. Voneinander abhängig sind nur die beiden anderen Größen. }} | ||
= Erstellung eines Dreiecksdiagrammes = | == Erstellung eines Dreiecksdiagrammes == | ||
{{Aufgaben-blau|1= Umsetzen einer Tabelle in ein Dreiecksdiagramm |2= | {{Aufgaben-blau|1= Umsetzen einer Tabelle in ein Dreiecksdiagramm |2= | ||
| Zeile 193: | Zeile 193: | ||
<br> | <br> | ||
= {{Schrift_grün|Auswertung von Dreiecksdiagramme}}n = | == {{Schrift_grün|Auswertung von Dreiecksdiagramme}}n == | ||
'''Nun betrachten wir ein anderes Dreiecksgidagramm:''' <br> | '''Nun betrachten wir ein anderes Dreiecksgidagramm:''' <br> | ||
| Zeile 241: | Zeile 241: | ||
}} | }} | ||
= {{Schrift_grün|Erläuterung: Auswertung und Interpretation von Dreiecksdiagrammen}} = | == {{Schrift_grün|Erläuterung: Auswertung und Interpretation von Dreiecksdiagrammen}} == | ||
{{Aufgaben-blau|1= Erläuterung: Auswertung und Interpretation von Dreiecksdiagrammen|2= | {{Aufgaben-blau|1= Erläuterung: Auswertung und Interpretation von Dreiecksdiagrammen|2= | ||
| Zeile 293: | Zeile 293: | ||
}} | }} | ||
< | <popup name="Eine mögliche Lösung"></popup> | ||
Version vom 17. Mai 2016, 16:11 Uhr
Vorlage:Schrift grün
Um die Abhängigkeit von zwei Größen in einem Diagramm darzustellen benutzt man üblicherweise ein x-y-Koordinatensystem. In vielen Fällen hängen aber drei auch mehr Größen voneinander ab. Speziell für drei Größen wie z.B.
- den primären, sekundären und tertiären Wirtschaftssektor oder
- die Anteile von Feldspat, Quarz und Glimmer in magmatischen Gesteinen
ist das sogenannte Dreiecksdiagramm eine übliche Darstellung.
Im folgenden Diagramm ist der Prozentanteil an Vollerwerbslandwirten, Zuerwerbslandwirten und Nebenerwerbslandwirten in der Bundesrepublik dargestellt.
Zur Begriffsklärung:
- Vollerwerbslandwirt: erzielt sein Einkommen zu 100 % aus der Landwirtschaft
- Zuerwerbslandwirt: der Anteil des Einkommens aus der Landwirtschaft beträgt mehr als 50 %
- Nebenerwerbslandwirt: der Anteil des Einkommens aus der Landwirtschaft beträgt weniger als 50 %
Vorlage:Schrift grün
Merke
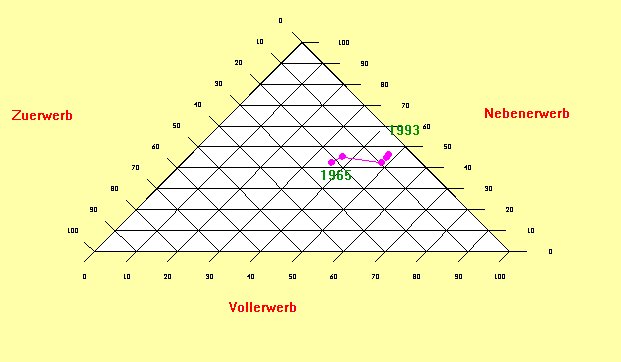
- Das Dreiecksdiagramm ist (üblicherweise ein gleichseitiges Dreieck) ein Diagramm, in dem man von drei Größen die Prozentanteile an der Summe der einzelnen Größen darstellt.
- In jedem Punkt ergibt sich als Summe der Prozentwerte der einzelnen Größen 100 %.
- Die Prozentanteile der einzelnen Größen liest man an den Parallele durch den Datenpunkt zur jeweils übernächsten Seite (gegen den Uhrzeigersinn) ab oder einfacher: vom Datenpunkt zu den Seiten des Dreiecks längs der Gitternetzlinien.
- Die Werte in einem Dreiecksdiagramm gestatten keinen Rückschluss auf Absolutwerte der einzelnen Größen.
<popup>
Lösung
Datei:Tabauswertung2.xls
</popup>
Merke
Bei der Darstellung einer zeitlichen Entwicklung kann man die Abhängikeit der drei Größen voneinander untersuchen. Ist die Kurve weitgehend (oder in Teilen) parallel zu einer der drei Seiten, so hat eine der drei Größen einen konstanten (im betrachteten Zeitraum konstanten) Anteil. Voneinander abhängig sind nur die beiden anderen Größen.
Erstellung eines Dreiecksdiagrammes
Vorlage:Schrift grünn
Nun betrachten wir ein anderes Dreiecksgidagramm:
Erläuterung der Begriffe:
In der Geologie, der Bodenkunde aber auch im Baustoffhandel unterscheiden man verschiedene Korngrößen. Dafür gibt es die sog. DIN 4022:
Da in Böden nicht nur ein Korngröße vertreten ist (Wir erforschen den Boden, beschreibt man die sog. Bodenart durch die Prozentanteile
der drei Korngrößengruppen Ton, Schluff und Sand. Je nach der Lage im Dreiecksdiagramm (nicht vollständige Begriffsdefinition) kennzeichnet man in Beschreibungen die Bodenart als schluffig sandigen Lehm, als lehmigen Sand, tonigen Schluff usw.
Vorlage:Schrift grün
Merke
Interpretieren des Diagrammes bedeutet das Verknüpfen der Daten des Diagrammes mit anderen Quellen, wie z.B. einem vorgegebenem Text, dem Atlas oder weiteren (anderen) Diagrammen. Es bedeutet Gründe für die zeitliche Entwicklung zu finden oder z. B. Gründe für die unterschiedlichen Anteile in den einzelnen Ländern zu finden.
<popup name="Eine mögliche Lösung"></popup>
