Vera 8 interaktiv/Mathematik/2009 Test III: Unterschied zwischen den Versionen
(Lösungen ergänzt) |
(bilder verlinkt) |
||
| Zeile 33: | Zeile 33: | ||
|- | |- | ||
|<div style="padding:10px;background:#ffffff;border:1px groove;"> | |<div style="padding:10px;background:#ffffff;border:1px groove;"> | ||
<big>'''Aufgabe 2 | <big>'''Aufgabe 2: Katzenfutter '''</big> | ||
In einem Werbeprospekt für einen Supermarkt ist folgender Ausschnitt zu finden. | In einem Werbeprospekt für einen Supermarkt ist folgender Ausschnitt zu finden. | ||
[[Datei:Vera8 Mathe 2009 III A2.jpg|left]] | |||
<br> | <br> | ||
<big>'''Aufgabe 2.1: Katzenfutter '''</big> | |||
Berechne, wie viel eine Dose dieses Katzenfutters normalerweise kostet. | Berechne, wie viel eine Dose dieses Katzenfutters normalerweise kostet. | ||
| Zeile 54: | Zeile 56: | ||
<big>'''Aufgabe 2.2: Katzenfutter '''</big> | <big>'''Aufgabe 2.2: Katzenfutter '''</big> | ||
Um wie viel Prozent wurde in dieser Aktion der Preis gesenkt? | |||
Welche Zahl liegt dem Ergebnis am nächsten? Kreuze an. | Welche Zahl liegt dem Ergebnis am nächsten? Kreuze an. | ||
| Zeile 240: | Zeile 242: | ||
|- | |- | ||
|<div style="padding:10px;background:#ffffff;border:1px groove;"> | |<div style="padding:10px;background:#ffffff;border:1px groove;"> | ||
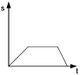
<big>'''Aufgabe 8: | <big>'''Aufgabe 8: Steckwürfelfiguren '''</big> | ||
Diese Figuren wurden jeweils aus vier kleinen Würfeln zusammengesteckt | Diese Figuren wurden jeweils aus vier kleinen Würfeln zusammengesteckt. | ||
[[Datei:Vera8 Mathe 2009 III A8.jpg|left]] | |||
<br> | |||
<big>'''Aufgabe 8.1: | Sie werden gut gemischt in ein Säckchen gefüllt. Es wird anschließend ohne hinzuschauen eine Figur aus dem Säckchen gezogen. | ||
<big>'''Aufgabe 8.1: Steckwürfelfiguren '''</big> | |||
Gib an, mit welcher Warscheinlichkeit die gezogene Figur einfarbig ist. | Gib an, mit welcher Warscheinlichkeit die gezogene Figur einfarbig ist. | ||
| Zeile 259: | Zeile 266: | ||
|- | |- | ||
|<div class="multiplechoice-quiz"> | |<div class="multiplechoice-quiz"> | ||
<big>'''Aufgabe 8.2: | <big>'''Aufgabe 8.2: Steckwürfelfiguren'''</big> | ||
Mit welcher Wahrscheinlichkeit enthält die gezogene Figur mindestens zwei helle Würfel? | Mit welcher Wahrscheinlichkeit enthält die gezogene Figur mindestens zwei helle Würfel? | ||
| Zeile 321: | Zeile 328: | ||
|- | |- | ||
|<div style="padding:10px;background:#ffffff;border:1px groove;"> | |<div style="padding:10px;background:#ffffff;border:1px groove;"> | ||
<big>'''Aufgabe 11: Kleinanzeigen'''</big> | |||
In einer Stadtillustrierten werden die Preise für Kleinanzeigen bei Privatkunden folgendermaßen berechnet: | |||
:1 - 5 Zeilen 10,00 € | |||
:Jede weitere Zeile 1,80€ | |||
Hier sind zwei Anzeigen: | |||
[[Datei:Vera8 Mathe 2009 III A11.jpg|left]] | |||
<br> | |||
<big>'''Aufgabe 11.1: Kleinanzeigen '''</big> | <big>'''Aufgabe 11.1: Kleinanzeigen '''</big> | ||
| Zeile 376: | Zeile 397: | ||
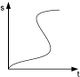
''s: Entfernung zu Peters Wohnung; t: Zeit ab Abfahrt von Peter von zu Hause'' | ''s: Entfernung zu Peters Wohnung; t: Zeit ab Abfahrt von Peter von zu Hause'' | ||
(! | (![[Datei:Vera8 Mathe 2009 III A12_Abb_a.jpg|80px]]) (![[Datei:Vera8 Mathe 2009 III A12_b.jpg|80px]]) ([[Datei:Vera8 Mathe 2009 III A12_c.jpg|80px]]) (![[Datei:Vera8 Mathe 2009 III A12_d.jpg|80px]]) (![[Datei:Vera8 Mathe 2009 III A12_e.jpg|80px]]) | ||
</div> | </div> | ||
| Zeile 486: | Zeile 507: | ||
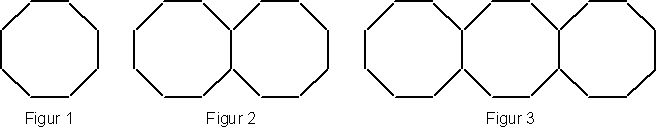
Streichhölzer werden wie folgt angeordnet. | Streichhölzer werden wie folgt angeordnet. | ||
[[Datei:Vera8 Mathe 2009 III A15.jpg|left]] | |||
<br> | |||
<big>'''Aufgabe 15.1: Streichhölzer '''</big> | <big>'''Aufgabe 15.1: Streichhölzer '''</big> | ||
| Zeile 499: | Zeile 524: | ||
</div> | </div> | ||
<big>'''Aufgabe 15.2: | |- | ||
|<div style="padding:10px;background:#ffffff;border:1px groove;"> | |||
<big>'''Aufgabe 15.2: Streichholzmuster '''</big> | |||
Stelle einen Term auf, mit dem man die Anzahl der Streichhölzer der n-ten Figur berechnen kann. | Stelle einen Term auf, mit dem man die Anzahl der Streichhölzer der n-ten Figur berechnen kann. | ||
| Zeile 507: | Zeile 534: | ||
}} | }} | ||
</div> | |||
</div> | </div> | ||
|- | |||
<big>'''Aufgabe 15.3: | |<div style="padding:10px;background:#ffffff;border:1px groove;"> | ||
<big>'''Aufgabe 15.3: Streichholzmuster '''</big> | |||
Bei einem anderen Muster wird die Anzahl der benötigten Streichhölzer für die n-te Figur durch den Term 3 - (n-1) · 2 beschrieben. | Bei einem anderen Muster wird die Anzahl der benötigten Streichhölzer für die n-te Figur durch den Term 3 - (n-1) · 2 beschrieben. | ||
| Zeile 517: | Zeile 546: | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
:z.B. | :z.B. | ||
:[[Datei:Vera8 Mathe 2009 III A15_lös.jpg]] | |||
}} | }} | ||
| Zeile 528: | Zeile 558: | ||
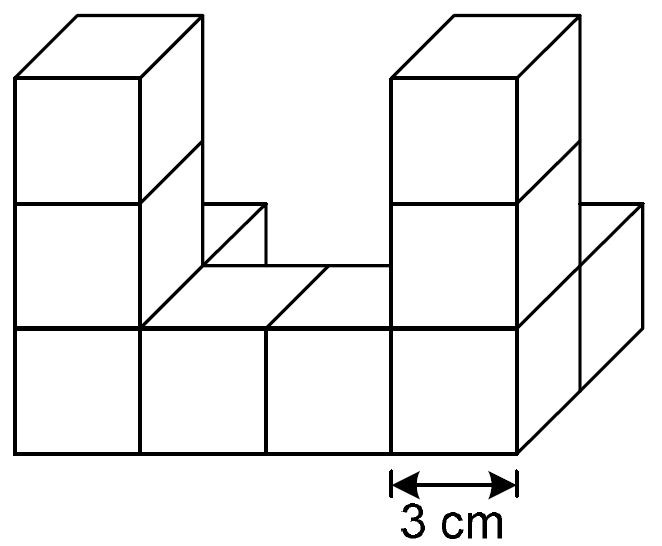
Der Körper ist aus gleichen Würfeln zusammengesetzt. | Der Körper ist aus gleichen Würfeln zusammengesetzt. | ||
[[Datei:Vera8 Mathe 2009 III A16.jpg]] | |||
<br> | |||
Berechne das Volumen des gesamten Körpers. Kreuze an. | Berechne das Volumen des gesamten Körpers. Kreuze an. | ||
| Zeile 539: | Zeile 572: | ||
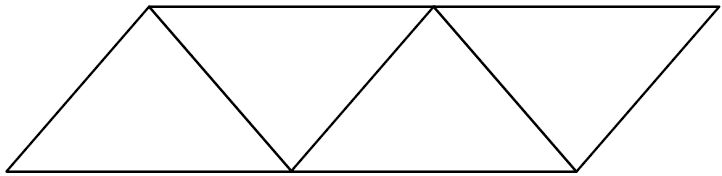
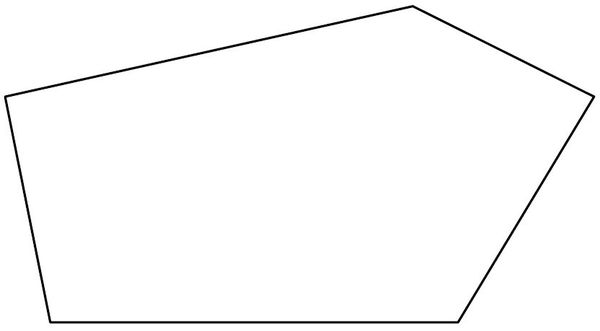
Begründe, weshalb die Innenwinkelsumme in einem Fünfeck 540° beträgt. Benutze dazu die gegebene Zeichnung. | Begründe, weshalb die Innenwinkelsumme in einem Fünfeck 540° beträgt. Benutze dazu die gegebene Zeichnung. | ||
[[Datei:Vera8 Mathe 2009 III A18.jpg|left]] | |||
<br> | |||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
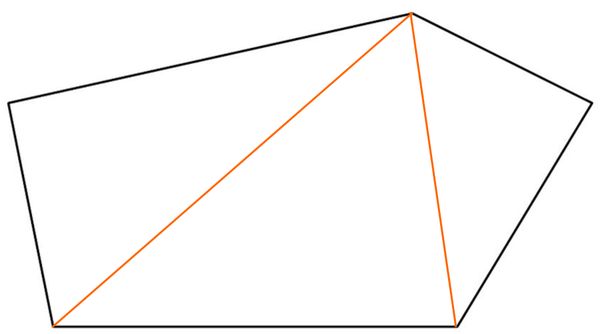
:Ein Fünfeck kann in 3 Dreiecke zerlegt werden (siehe Zeichnung). Die Innenwinkelsumme jedes Dreiecks beträgt 180°. Also beträgt die Innenwinkelsumme des Fünfecks 3 ·180° = 540° | :Ein Fünfeck kann in 3 Dreiecke zerlegt werden (siehe Zeichnung). Die Innenwinkelsumme jedes Dreiecks beträgt 180°. Also beträgt die Innenwinkelsumme des Fünfecks 3 ·180° = 540° | ||
:[[Datei:Vera8 Mathe 2009 III A18_lös.jpg|left]] | |||
}} | }} | ||
Version vom 28. Februar 2010, 16:12 Uhr
Vorsicht: Baustelle!
Aufgabe 1: LKW-Ladung Herr Zuse besitzt einen Lastkraftwagen (LKW) mit einer erlaubten Nutzlast von 3,5t. Wie viele Kisten zu je 30kg darf Herr Zuse höchstens auf seinen LKW laden?
| ||||||||||||||||||||
|
| ||||||||||||||||||||
|
Aufgabe 2.2: Katzenfutter Um wie viel Prozent wurde in dieser Aktion der Preis gesenkt? Welche Zahl liegt dem Ergebnis am nächsten? Kreuze an. (!25%) (39%) (!53%) (!61%) (!63%) | ||||||||||||||||||||
Aufgabe 3.1: Mittig Welche Zahl liegt genau in der Mitte zwischen 99 und 999? (!449) (!450) (!500) (549) (!550)
| ||||||||||||||||||||
Aufgabe 3.2: Mittig Gib zwei andere Zahlen an, in deren Mitte genau dieselbe Zahl liegt wie bei Teilaufgabe 3.1.
| ||||||||||||||||||||
Aufgabe 4: Sonderangebot Ein 200 g-Glas löslicher Kaffee kostet in einem Geschäft normalerweise 7,90 €. Sonderangebot A: Der Preis für das 200 g-Glas wird um 20% gesenkt. Sonderangebot B: Es wird ein Glas mit 20% mehr Inhalt zum gleichen Preis von 7,90 € angeboten. Welches ist für einen Kunden das günstigere Angebot? Begründe deine Antwort.
| ||||||||||||||||||||
Aufgabe 5: Quersumme Die Quersumme einer zweiziffrigen Zahl ist 9. Vertauscht man die Ziffern, so ist die Differnez der neu gebildeten und der ursprünglichen Zahl gleich 45. Bestimme die Zahl. Schreibe auf, wie du vorgegangen bist.
| ||||||||||||||||||||
Aufgabe 6.1: Quiz Birgit nahm an einem Quiz teil, bei dem sie insgesamt 18 Fragen zu beantworten hatte. Für jede richtige Antwort erhielt sie einen Pluspunkt, für jede falsche Antwort einen Minuspunkt. Am Endes des Quiz wurden die Plus- und Minuspunkte miteinander verrechnet und Birgit verblieben acht Pluspunkte. Wie viele Fragen hatte Birgit insgesamt richtig beantworten?
Roland hatte bei diesem Quiz sieben Fragen richtig beantwortet. Wie viele Punkte hatte er insgesamt, nachdem Plus- und Minuspunkte miteinander verrechnet wurden?
Ist es möglich, bei diesem Quiz neun Punkte als Endergebnis zu erhalten? Begründe deine Antwort.
| ||||||||||||||||||||
Aufgabe 7: Internetauktion Bei einer Internetauktion beobachtet Rolf die Preisentwicklung für Notebooks. Insgesamt werden neun Notebooks des gleichen Typs versteigert. Rolf hat sich folgende Endpreise für die Notebooks aufgeschrieben:
Wie groß ist der Preisunterschied zwischen dem teuersten und billigstem Notebook?
Wie viel Prozent kostet das teuerste notebook mehr als das billigste?
Gib den durchschnittlichen Preis der neun Notebooks an.
| ||||||||||||||||||||
Aufgabe 8: Steckwürfelfiguren Diese Figuren wurden jeweils aus vier kleinen Würfeln zusammengesteckt.
Sie werden gut gemischt in ein Säckchen gefüllt. Es wird anschließend ohne hinzuschauen eine Figur aus dem Säckchen gezogen.
Gib an, mit welcher Warscheinlichkeit die gezogene Figur einfarbig ist.
| ||||||||||||||||||||
Aufgabe 8.2: Steckwürfelfiguren Mit welcher Wahrscheinlichkeit enthält die gezogene Figur mindestens zwei helle Würfel? (!) (!) (!) ()
| ||||||||||||||||||||
Aufgabe 9: Gummibären Nach Herstellerangaben werden vor dem Abfüllen von Gummibären in Tüten die Bären folgendermaßen durchgemischt: Je ein Sechstel grüne, gelbe, weiße und orangefarbene Bären und ein Drittel rote Bären. Die Hälfte der roten Bären schmeckt nach Erdbeere, die andere Hälfte nach Himbeeren.
Jan greift sich mit geschlossenen Augen ein Gummibärchen aus einer frischen geöffneten Tüte. Mit welcher Wahrscheinlichkeit hat es Himbeergeschmack?
| ||||||||||||||||||||
Aufgabe 9.2: Gummibären Fünf Gummibärchen wiegen 10g. Kreuze an mit wie vielen grünen Gummibärchen man in einer 1000-g-Tüte etwa rechnen kann. (!20) (!60) (80) (!160)(!330) | ||||||||||||||||||||
Aufgabe 9.3: Gummibären: Luisa hat eine Minitüte bekommen, mit 4 grünen, 2 roten, 3 orangefarbenen, 2 weißen und einem gelben Gummibärchen. Sie sagt: "Daran sieht man, dass die Angaben des Herstellers über die Mischung der Farben gar nicht stimmen können." Erkläre, was Luisa damit meint, und beurteile ihre Aussage.
| ||||||||||||||||||||
Aufgabe 11.2: Kleinanzeige Wie teuer war die zweite Anzeige? Kreuze an. (!10,00€) (!19,00€) (!23,40€) (24,40€) (!26,00€) | ||||||||||||||||||||
Aufgabe 11.3: Kleinanzeigen Eine dritte Anzeige hat 38,80 € gekostet. Wie viele Zeilen hatte sie?
| ||||||||||||||||||||
Aufgabe 11.4: Kleinanzeigen Wenn eine Anzeige ganz in fett und gelb unterlegt gedruckt werden soll, kostet das 15,00 € mehr. Um wie viel Prozent verteuert sich dadurch die dritte Anzeige? (!um ca. 15%) (!um ca. 28%) (um ca. 39%) (!um ca. 61%) (!um ca. 72%) | ||||||||||||||||||||
Aufgabe 12: Fahrrad Peter wollte mit dem Fahrrad zu seinem Freund Paul fahren. Auf dem Weg dorthin traf er Tina, die ihm die Lösung der Hausaufgaben erklärte. Anschließend fuhr er weiter zu Paul, den er nicht antraf. Jetzt ist er auf dem Weg nach Hause. Welcher Graph passt zu dieser Geschichte? Kreuze an. s: Entfernung zu Peters Wohnung; t: Zeit ab Abfahrt von Peter von zu Hause | ||||||||||||||||||||
Aufgabe 13: Kanutour Die 21 Schüler der Klasse 8e möchten eine Kanutour machen. Leider sind im Kanuclub nicht genügend Kanus vorhanden. Daher möchte Frau Krell einen Kleintransporter mit Anhänger mieten, um weitere Kanus zu transportieren. In der Zeitung findet Frau Krell die beiden folgenden Angebote.
Vergleiche die beiden Angebote. Berate Frau Krell bei der Wahl eines Angabots für einen Kleintransporter mit Anhänger. Notiere deine Argumente.
| ||||||||||||||||||||
Aufgabe 13.2: Kanutour Im Internet findet Frau Krell das Angebot des Autovermieters "Autoscout". Dieser verlangt eine einmalige Grundgebühr von 120 € und eine Kilometerpauschale von 30 Cent. In desem Angebot sind 100 Freikilometer enthalten. Mit welcher Gleichung kann man die Kosten beschreiben, wenn man mehr als 100 Kilometer fährt? x soll dabei die Gesamtzahl der gefahrenen Kilometer sein. Kreuze an. (y = 0,3 · [x - 100] + 120) (!y = 0,3 · x + 120) (!y = 0,3 · [x + 100] + 120) (!y = 30 · [x - 100] + 120) | ||||||||||||||||||||
Aufgabe 14.1: Mitschüler In der Klasse 8a sind insgesamt 25 Schülerinnen und Schüler. Es sind 7 Jungen mehr als Mädchen. Wie viele Mädchen sind in der Klasse? Kreuze an. (!6) (!7) (9) (!16) (!18) | ||||||||||||||||||||
Aufgabe 14.2: Mitschüler In der Klasse 8b mit insgesamt 28 Schülerinnen und Schülern sind 3 mal so viele Mädchen wie Jungen. Beschreibe diese Situation mit einer Gleichung.
| ||||||||||||||||||||
Aufgabe 14.3: Mitschüler Steffi ist in der 8c. In dieser Klasse sind insgesamt 31 Schülerinnen und Schüler. Steffi behauptet: "Wenn zu meiner Klasse ein Mädchen hinzukäme und ein Junge die Klasse verließe, wären gleich viele Jungen und Mädchen in der Klasse." Erläutere, warum Steffis Behauptung nicht richtig sein kann.
| ||||||||||||||||||||
Aufgabe 15.2: Streichholzmuster Stelle einen Term auf, mit dem man die Anzahl der Streichhölzer der n-ten Figur berechnen kann.
| ||||||||||||||||||||
Aufgabe 18: Innenwinkel Begründe, weshalb die Innenwinkelsumme in einem Fünfeck 540° beträgt. Benutze dazu die gegebene Zeichnung.
|