Lineare Funktionen im Aktiv-Urlaub/Wertetabelle und Funktionsgleichung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 23: | Zeile 23: | ||
===Punktprobe: Liegt der Punkt auf der Geraden?=== | ===Punktprobe: Liegt der Punkt auf der Geraden?=== | ||
{{Box|Bootsverleih|[[Datei:Boat-g79745909a 1280.png|rahmenlos|rechts|200x200px]] | {{Box|Bootsverleih- Aufagbe 1|[[Datei:Boat-g79745909a 1280.png|rahmenlos|rechts|200x200px]]Tom und Lisa möchten im Urlaub ein Tretboot ausleihen. Die Grundgebühr beträgt 5€, pro Stunde zahlen sie 2€ Miete.<br> | ||
Sie leihen für 3 Stunden ein Tretboot. Der Bootsverleiher rechnet den Preis 10€ aus. Kann das sein?<|Meinung}}<br> | |||
Bei der Punktprobe entscheidest du rechnerisch, ob ein Punkt auf dem Funktionsgraphen liegt. | Bei der Punktprobe entscheidest du rechnerisch, ob ein Punkt auf dem Funktionsgraphen liegt. | ||
| Zeile 78: | Zeile 77: | ||
===Fehlende Koordinate eines Punktes der Funktion berechnen=== | ===Fehlende Koordinate eines Punktes der Funktion berechnen=== | ||
{{Box| | {{Box|Bootsverleih - Aufgabe 2|[[Datei:Boat-g79745909a 1280.png|rechts|rahmenlos|200x200px]]Tom und Lisa möchten im Urlaub ein Tretboot ausleihen. Die Grundgebühr beträgt 5€, pro Stunde zahlen sie 2€ Miete.<br> | ||
Tom und Lisa leihen ein Tretboot für 1,5 Stunden. Wie viel müssen sie bezahlen?|Meinung | Tom und Lisa leihen ein Tretboot für 1,5 Stunden. Wie viel müssen sie bezahlen?|Meinung}} | ||
}}Du kannst mithilfe der Funktionsgleichung fehlende Koordinaten berechnen. | Du kannst mithilfe der Funktionsgleichung fehlende Koordinaten berechnen. | ||
'''1. Möglichkeit: <span style="color:red">x</span>-Koordinate ist gegeben''' | '''1. Möglichkeit: <span style="color:red">x</span>-Koordinate ist gegeben''' | ||
| Zeile 117: | Zeile 116: | ||
Sie haben das Boot für 2,5 Stunden geliehen. | Sie haben das Boot für 2,5 Stunden geliehen. | ||
<br /><div class="grid"><div class="width-1-2">Zusammenfassung:{{#ev:youtube|iV-ysofefkg|460|center|||start=185&end=409}}</div><div class="width-1-2">noch mehr Beispiele:{{#ev:youtube|Gi1Dj4kzL20|460|center|||start=135&end=302}}</div></div>{{Box|Übung 3: Fehlende Koordinate bestimmen|Bestimme in der folgenden App jeweils die fehlende Koordinate.|Üben}} | <br /> | ||
{{LearningApp| app = pz6auqgia20| width = 100%| | <div class="grid"><div class="width-1-2">Zusammenfassung:{{#ev:youtube|iV-ysofefkg|460|center|||start=185&end=409}}</div><div class="width-1-2">noch mehr Beispiele:{{#ev:youtube|Gi1Dj4kzL20|460|center|||start=135&end=302}}</div></div> | ||
{{Box|Übung 3: Fehlende Koordinate bestimmen|Bestimme in der folgenden App jeweils die fehlende Koordinate.|Üben}} | |||
{{LearningApp| app = pz6auqgia20| width = 100%| height = 600px}} | |||
{{Box|Übung 4: Fehlende Koordinaten bestimmen und Punktprobe|Löse nun S. 137 Nr. 8 und 9.|Üben}} | {{Box|Übung 4: Fehlende Koordinaten bestimmen und Punktprobe|Löse nun S. 137 Nr. 8 und 9.|Üben}} | ||
{{Lösung versteckt|Denke daran: P(x/y) Der erste Wert gibt immer die x- und der zweite Wert die y-Koordinate an. Setze nun entweder x oder y in die Gleichung ein und berechne den fehlenden Wert.|Tipp zu Nr. 8|Tipp ausblenden}}{{Lösung versteckt|Hier findest du die Lösungen <u>bunt gemischt</u>: <br> | {{Lösung versteckt|Denke daran: P(x/y) Der erste Wert gibt immer die x- und der zweite Wert die y-Koordinate an. Setze nun entweder x oder y in die Gleichung ein und berechne den fehlenden Wert.|Tipp zu Nr. 8|Tipp ausblenden}}{{Lösung versteckt|Hier findest du die Lösungen <u>bunt gemischt</u>: <br> | ||
| Zeile 137: | Zeile 140: | ||
===Aufstellen der Funktionsgleichung durch den Punkt P mit m oder b gegeben=== | ===Aufstellen der Funktionsgleichung durch den Punkt P mit m oder b gegeben=== | ||
{{Box|Übung 6: Aufstellen der Funktionsgleichung|Löse S. 130 Nr. 9 (zeichnerisch UND rechnerisch) und S. 131 Nr. 13. Gegeben ist ein Punkt und die Steigung bzw. der y-Achsenabschnitt b. Wie kannst du vorgehen?|Üben | |||
}}{{Lösung versteckt|1=Die vorangegangenen Übungen zur "Punktprobe" können dir helfen: | {{Box|Übung 6: Aufstellen der Funktionsgleichung|Löse S. 130 Nr. 9 (zeichnerisch UND rechnerisch) und S. 131 Nr. 13. Gegeben ist ein Punkt und die Steigung bzw. der y-Achsenabschnitt b. Wie kannst du vorgehen?|Üben}} | ||
{{Lösung versteckt|1=Die vorangegangenen Übungen zur "Punktprobe" können dir helfen: | |||
Sezte in die allgemeine Funktionsgleichung f(x) = mx + b die gegebenen Größen ein und löse nach der gesuchten Größe auf.|2=Tipp 1|3=Verbergen}}{{Lösung versteckt|1=Zu Nr. 9: Wenn die Gerade <b>parallel</b> zur Geraden von f(x)= 1,5x + 1 verläuft, haben die Geraden <b>dieselbe Steigung</b>! Also ist m = 1,5 gegeben. Außerdem hast du den Punkt P(2I6) gegeben. Gesucht ist b. | Sezte in die allgemeine Funktionsgleichung f(x) = mx + b die gegebenen Größen ein und löse nach der gesuchten Größe auf.|2=Tipp 1|3=Verbergen}}{{Lösung versteckt|1=Zu Nr. 9: Wenn die Gerade <b>parallel</b> zur Geraden von f(x)= 1,5x + 1 verläuft, haben die Geraden <b>dieselbe Steigung</b>! Also ist m = 1,5 gegeben. Außerdem hast du den Punkt P(2I6) gegeben. Gesucht ist b. | ||
Setze die gegebenen Größen ein und löse nach b auf.|2=Tipp zu Nr. 9|3=Verbergen}}{{Lösung versteckt|Hilfen bietet das nachfolgende Video:{{#ev:youtube|KnOdPP4gqmc}}|Video mit Beispielaufgaben|Verbergen}}<br /> | Setze die gegebenen Größen ein und löse nach b auf.|2=Tipp zu Nr. 9|3=Verbergen}}{{Lösung versteckt|Hilfen bietet das nachfolgende Video:{{#ev:youtube|KnOdPP4gqmc}}|Video mit Beispielaufgaben|Verbergen}}<br /> | ||
===Schnittpunkte mit den Koordinatenachsen bestimmen=== | ===Schnittpunkte mit den Koordinatenachsen bestimmen=== | ||
{{Box| | |||
Nach welcher Zeit ist der Pool leer?|Meinung | {{Box|Pool - Aufgabe 3|[[Datei:Smartphone-g0b5325198 1280.png|rechts|rahmenlos|200x200px]]Der Pool des Hotels muss geleert werden. Zu Beginn steht das Wasser 2 m hoch. Der Wasserstand sinkt stündlich um 10 cm.<br> | ||
}}{{#ev:youtube|KnOdPP4gqmc}}{{Box|Schnittpunkte mit den Koordinatenachsen | Nach welcher Zeit ist der Pool leer?|Meinung}} | ||
| 2 = Für den Schnittpunkt P<sub>y</sub> mit der y-Achse (y-Achsenabschnitt) setzen wir x = 0 in die Funktionsgleichung ein berechnen b. | {{#ev:youtube|KnOdPP4gqmc}} | ||
{{Box|Schnittpunkte mit den Koordinatenachsen| 2 = Für den Schnittpunkt P<sub>y</sub> mit der y-Achse (y-Achsenabschnitt) setzen wir x = 0 in die Funktionsgleichung ein berechnen b. | |||
P<sub>y</sub> (0|b) | P<sub>y</sub> (0|b) | ||
Für den Schnittpunkt N mit der x-Achse (<b>Nullstelle</b>) setzen wir f(x) = 0 (oder y = 0) in die Funktionsgleichung ein und lösen die Gleichung nach x auf. | Für den Schnittpunkt N mit der x-Achse (<b>Nullstelle</b>) setzen wir f(x) = 0 (oder y = 0) in die Funktionsgleichung ein und lösen die Gleichung nach x auf. | ||
N (x<sub>N</sub>I0) | N (x<sub>N</sub>I0)| 3 = Merksatz}} | ||
| 3 = Merksatz | [[Datei:Übersicht_Schnittpunkte_mit_den_Koordinatenachsen.png|Übersicht Schnittpunkte mit den Koordinatenachsen]] | ||
}}[[Datei:Übersicht_Schnittpunkte_mit_den_Koordinatenachsen.png|Übersicht Schnittpunkte mit den Koordinatenachsen]]{{LearningApp | {{LearningApp| app = pu8028csj20| width = 100%| height = 400px}} | ||
| app = pu8028csj20 | {{Box|Übung 7: Schnittpunkte mit den Koordinatenachsen|Löse S. 137 Nr. 7|Üben} | ||
| width = 100% | {{Lösung versteckt|{{Lösung versteckt|1=Nullstelle (Schnittpunkt mit der x-Achse): f(x) = 0, also -x+4 = 0 | ||
| height = 400px | |||
}}{{Box|Übung 7: Schnittpunkte mit den Koordinatenachsen|Löse S. 137 Nr. 7|Üben | |||
y-Achsenabschnitt (Schnittpunkt mit der y-Achse): x = 0, also f(0) = -0+4 | y-Achsenabschnitt (Schnittpunkt mit der y-Achse): x = 0, also f(0) = -0+4 | ||
Version vom 2. Mai 2022, 13:31 Uhr
2.3) Zusammenhang zwischen Wertetabelle und Funktionsgleichung
Wiederholung: Erstellen einer Wertetabelle mithilfe der Funktionsgleichung
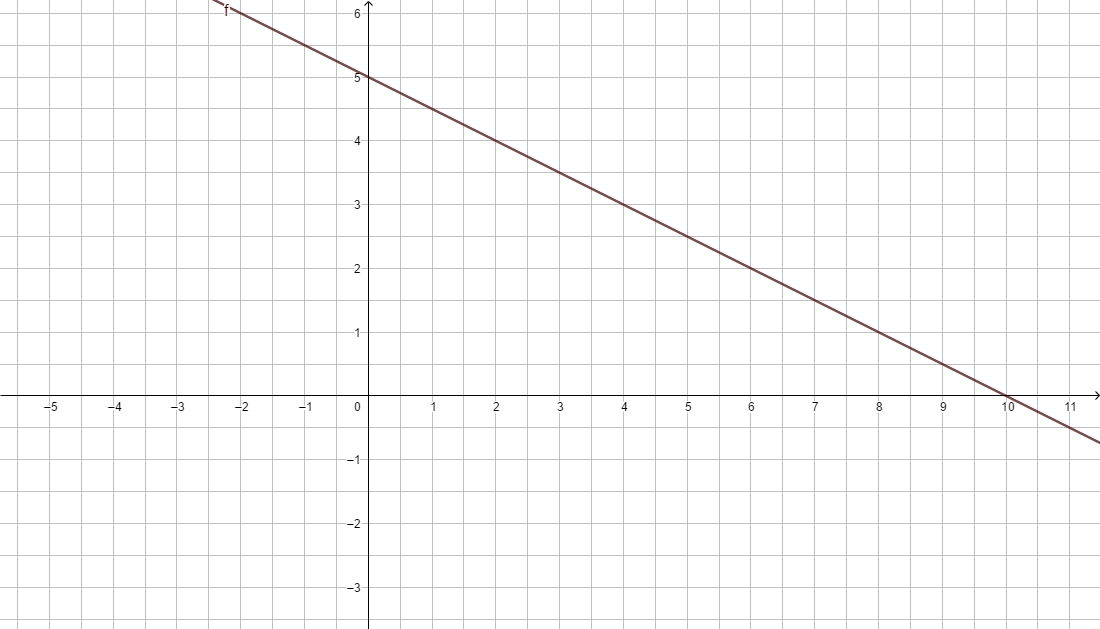
Du hast in den Einführungsbeispielen schon Wertetabellen erstellt. Schauen wir uns das Beispiel zum Bootsverleih noch einmal an. Die Funktionsgleichung lautet f(x) = 2x + 5
Um nun eine Wertetabelle zu erstellen, setze für x verschiedene Werte ein und berechne den zugehörigen y-Wert, den Funktionswert. Erinnerung: Werte von Termen berechnen (7. Klasse)

Das Video fasst das Vorgehen noch einmal zusammen:
Gib die Funktionsgleichungen bei GeoGebra ein und prüfe, ob die von dir errechneten Punkte auf dem Graphen der Funktion liegen.
https://www.geogebra.org/graphing
Punktprobe: Liegt der Punkt auf der Geraden?
Bei der Punktprobe entscheidest du rechnerisch, ob ein Punkt auf dem Funktionsgraphen liegt.
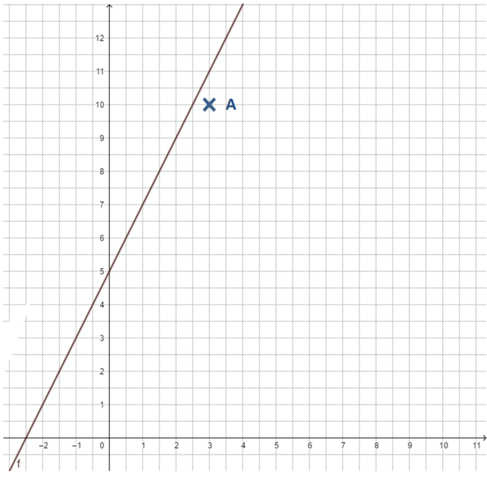
geg: Punkt A(3|10); Funktion f(x) = 2x + 5
ges: Liegt der Punkt A auf dem Graphen der Funktion?
In der Zeichnung erkennen wir sofort, dass dies nicht der Fall ist.
Wie können wir rechnerisch prüfen, ob ein Punkt auf dem Graphen der Funktion liegt?
Schreibe die nachfolgende Rechnung in dein Heft.Gegeben ist die Funktionsgleichung y = 2x + 5. Liegt der Punkt A(3|10) auf dem Graphen der Funktion?
(Hier ist es leichter y statt f(x) zu schreiben, der Zusammenhang zu den Koordinaten des Punktes sind dann leichter zu erkennen.)
Idee: Setze die Koordinaten des Punktes in die Funktionsgleichung ein und prüfe, ob die Gleichung erfüllt wird.
y= 2x + 5 A(3|10)
10 = 2·3 + 5
10 = 6 + 5
10 = 11 (f)
Es ergibt sich eine falsche Aussage, die Gleichung ist nicht erfüllt, also liegt der Punkt nicht auf dem Graphen. Wir prüfen ebenso, ob der Punkt B(4|13) auf der Geraden liegt:
Punktprobe:
y = 2x + 5 B(4|13)
13 = 2·4 + 5
13 = 8 + 5
13 = 13 (w)
Es ergibt sich eine wahre Aussage, die Gleichung ist erfüllt, also liegt der Punkt auf dem Graphen.
Das folgende Video fasst noch einmal zusammen:
Fehlende Koordinate eines Punktes der Funktion berechnen
Du kannst mithilfe der Funktionsgleichung fehlende Koordinaten berechnen.
1. Möglichkeit: x-Koordinate ist gegeben
geg: x = 1,5 und f(x) = 2x+5
ges: zugehöriger y-Wert
Setze die x-Koordinate in die Funktionsgleichung ein und berechne: f(x) = 2x + 5
y = 2·1,5 + 5
= 3 + 5
= 8 P(1,5|8)
Sie müssen 8€ bezahlen.
2. Möglichkeit: y-Koordinate ist gegeben:
Tom und Lisa bezahlen 10 €. Wie lange haben sie das Tretboot ausgeliehen?
geg: y = 10 und f(x) = 2x+5
ges: zugehörige x-Koordinate
Setze die y-Koordinate in die Funktionsgleichung ein und löse nach x auf:
f(x) = 2x + 5
10 = 2x + 5 |-5
5 = 2x |:2
2,5 = x P(2,5|10)
Sie haben das Boot für 2,5 Stunden geliehen.
Hier findest du die Lösungen bunt gemischt:
- fehlende x-Koordinate: 1; 5,5; 8
- fehlende y-Koordinate: -2; 7; 3
Denke daran: P(x/y) Der erste Wert gibt immer die x- und der zweite Wert die y-Koordinate an. Setze nun die entsprechenden Werte für x und y in die Gleichung ein.
- Erhältst du eine wahre Aussage, z.B. 5 = 5, so liegt der Punkt auf dem Funktionsgraphen.
- Erhältst du eine falsche Aussage, z.B. 5 = 8, so liegt der Punkt nicht auf dem Funktionsgraphen.
Hier findest du die Lösungen: (nicht in der richtigen Reihenfolge)
- Punkt A liegt einmal auf dem Graphen, zweimal nicht.
- Punkt B liegt einmal auf dem Graphen, zweimal nicht.
- Punkt C liegt zweimal auf dem Graphen, einmal nicht.
Bearbeite die Übungen auf den folgenden Seiten:
http://realmath.de/Neues/Klasse8/linearefunktion/koordberechnen.php
Aufstellen der Funktionsgleichung durch den Punkt P mit m oder b gegeben
Die vorangegangenen Übungen zur "Punktprobe" können dir helfen:
Sezte in die allgemeine Funktionsgleichung f(x) = mx + b die gegebenen Größen ein und löse nach der gesuchten Größe auf.Zu Nr. 9: Wenn die Gerade parallel zur Geraden von f(x)= 1,5x + 1 verläuft, haben die Geraden dieselbe Steigung! Also ist m = 1,5 gegeben. Außerdem hast du den Punkt P(2I6) gegeben. Gesucht ist b.
Setze die gegebenen Größen ein und löse nach b auf.
Schnittpunkte mit den Koordinatenachsen bestimmen
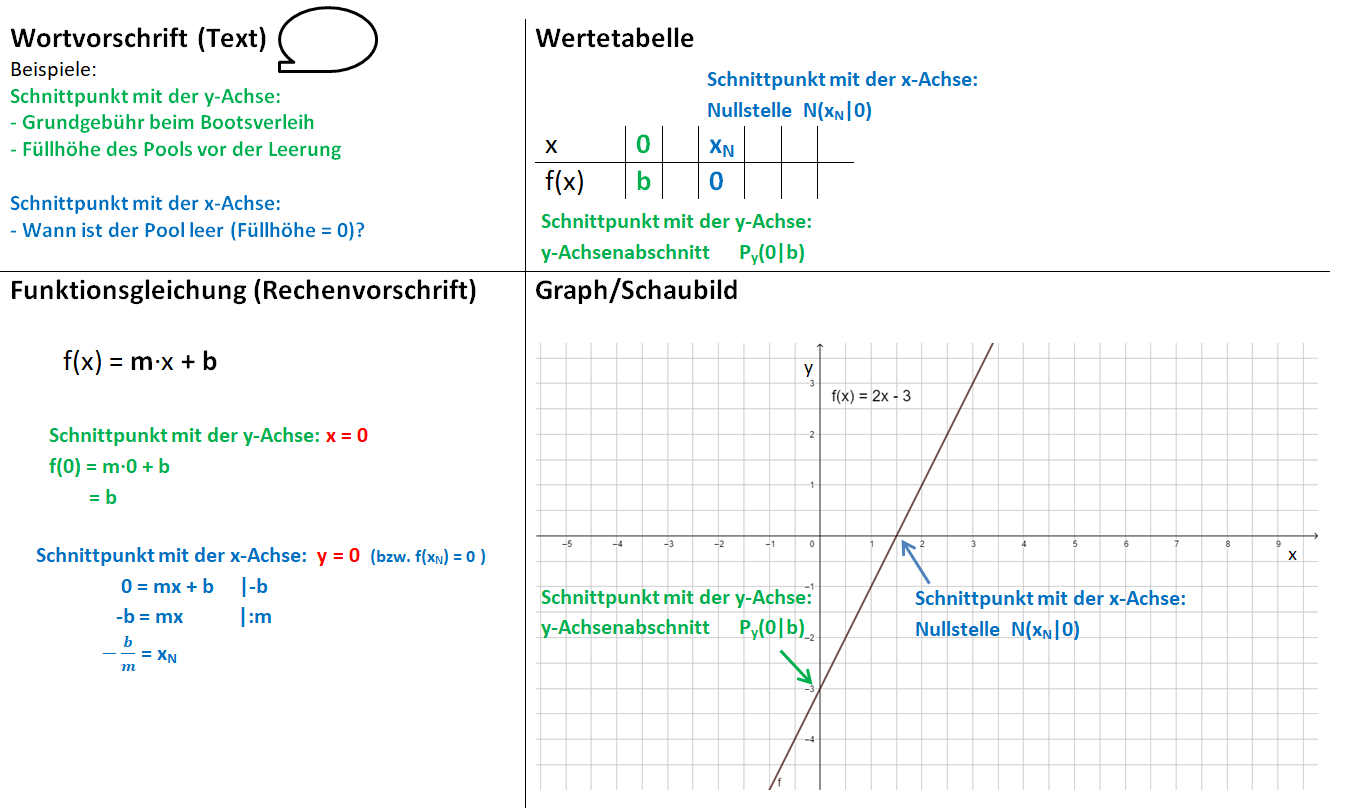
Für den Schnittpunkt Py mit der y-Achse (y-Achsenabschnitt) setzen wir x = 0 in die Funktionsgleichung ein berechnen b.
Py (0|b)
Für den Schnittpunkt N mit der x-Achse (Nullstelle) setzen wir f(x) = 0 (oder y = 0) in die Funktionsgleichung ein und lösen die Gleichung nach x auf.
N (xNI0)
{{Box|Übung 7: Schnittpunkte mit den Koordinatenachsen|Löse S. 137 Nr. 7|Üben}
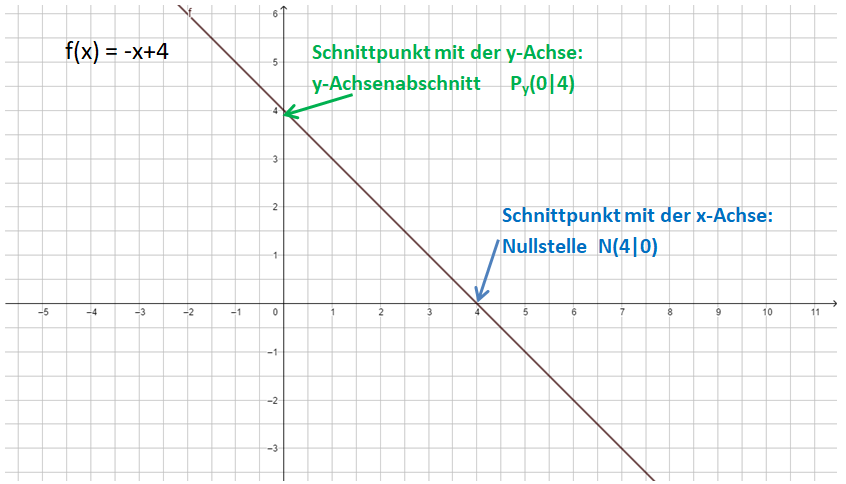
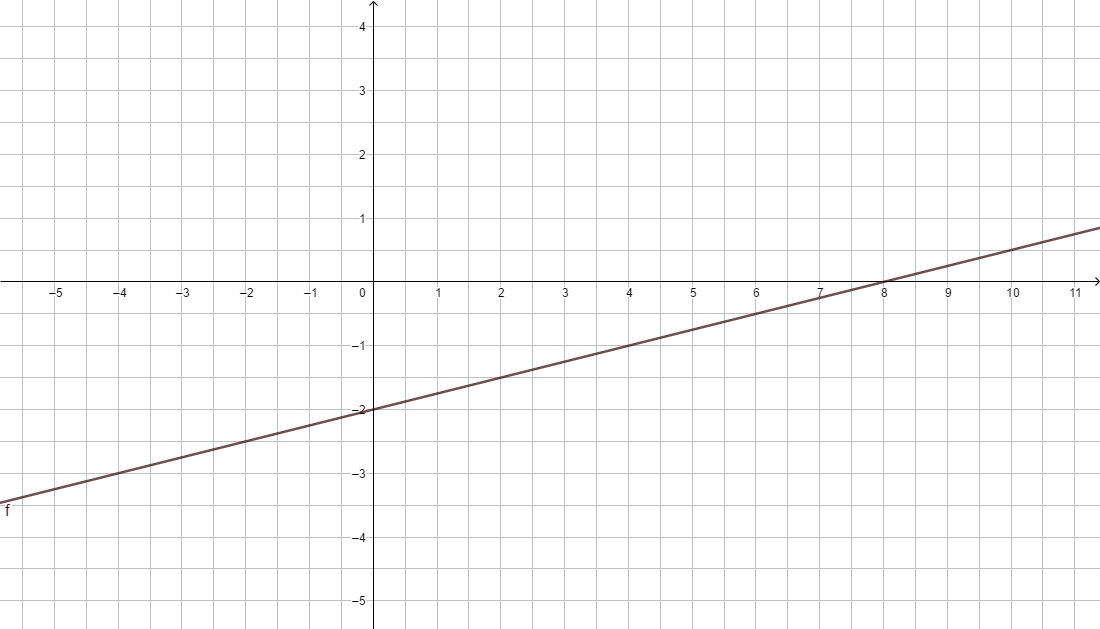
Nullstelle (Schnittpunkt mit der x-Achse): f(x) = 0, also -x+4 = 0
y-Achsenabschnitt (Schnittpunkt mit der y-Achse): x = 0, also f(0) = -0+4
Prüfe dein Ergebnis mithilfe von GeoGebra https://www.geogebra.org/graphing . Gib dort die Funktionsgleichung ein und vergleiche deine rechnerischen Lösungen mit dem Graphen. Wo schneidet der Graph die Koordinatenachsen?