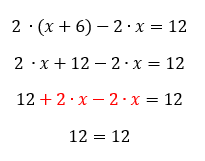Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Strukturänderung von Termen: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
BiaMa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
BiaMa (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 33: | Zeile 33: | ||
</div> | </div> | ||
<br /> | |||
<center>'''Wenn du noch Fragen zu Potenzen hast, sieh dir das Video unter folgendem Link an.'''</center><br /> | <center>'''Wenn du noch Fragen zu Potenzen hast, sieh dir das Video unter folgendem Link an.'''</center><br /> | ||
{{#ev:youtube|_7B_IFlFZAw|800|center}} | {{#ev:youtube|_7B_IFlFZAw|800|center}} | ||
Version vom 28. März 2022, 20:47 Uhr
Termstrukturen noch genauer!
In diesem Kapitel betrachten wir Termstrukuren noch ein bisschen genauer. Das Erkennen der Termstruktur ist wichtig, um genauer damit arbeiten zu können.
Merke
Jeder Term besitzt eine Grob- und eine Feinstruktur. Durch eine genaue Untersuchung des Terms kannst du diese Struktur erkennen. Eine Termstrukur setzt sich aus zusammenhängenden Rechenoperationen von Zahlen und/ oder Variablen zusammen. Außerdem kann die Struktur von Termen verändert werden.
Aufgabe 1
Löse folgende Aufgabe zu Termstrukturen. Die Aufgabe ist 1 Punkt Wert. Wenn du die Aufgaben richtig gelöst hast, dann darfst du den Punkt in deine Punktetabelle übertragen.
Aufgabe 2
In dieser Aufgabe sollst du geschüttelte Wörter wieder richtig zusammenfügen. Die Aufgabe ist 1 Punkt Wert. Wenn du die Aufgaben richtig gelöst hast, dann darfst du den Punkt in deine Punktetabelle übertragen. Benötigst du mehr als 3 Versuche, bekommst du leider keinen Punkt für diese Aufgabe.
Termstrukturen können durch Herausheben eines gemeinsamen Faktors oder durch Ausmultiplizieren, Erweitern oder Kürzen anders dargestellt werden.
Aufgabe 3
Löse folgende Aufgabe zu Termstrukturen. Die Aufgabe ist 1 Punkt Wert. Wenn du die Aufgaben richtig gelöst hast, dann darfst du den Punkt in deine Punktetabelle übertragen.
| Herausheben | 15ab + 21a = 3a ⋅ (5b + 7) | |
| Ausmultiplizieren | (5 - 4b) ⋅ (2a + 3b) = 10a + 15b -8ab - 12b² | 3 ⋅ (a - 5b) + 2ab = 3a - 15b + 2ab |
| Erweitern | ||
| Kürzen |
Erkundung 1: Zaubertrick
Denke an eine beliebige Zahl. Addiere 6 dazu und verdopple nun deine Zahl. Anschließend subtrahiere das doppelte deiner Zahl. Das Ergebnis ist 12. Wieso klappt das für jede Zahl?
Überlege mit deinem/deiner SitznachbarIn.