Vektorrechnung/WHG Q1 Kurze Übungen zu Pfeilen und Vektoren: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 61: | Zeile 61: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
* 1 und | * 1 und 12 ; 5 und 10 | ||
* 3, 4, 8 und 9 ; 2, 6 und 7 | * 3, 4, 8 und 9 ; 2, 6 und 7 | ||
* 5, 11 und 13 bzw. 10, 11 und 13 ; 2 und 9 | * 5, 11 und 13 bzw. 10, 11 und 13 ; 2 und 9 | ||
Version vom 22. September 2020, 19:06 Uhr
Pfeile
Übung 1
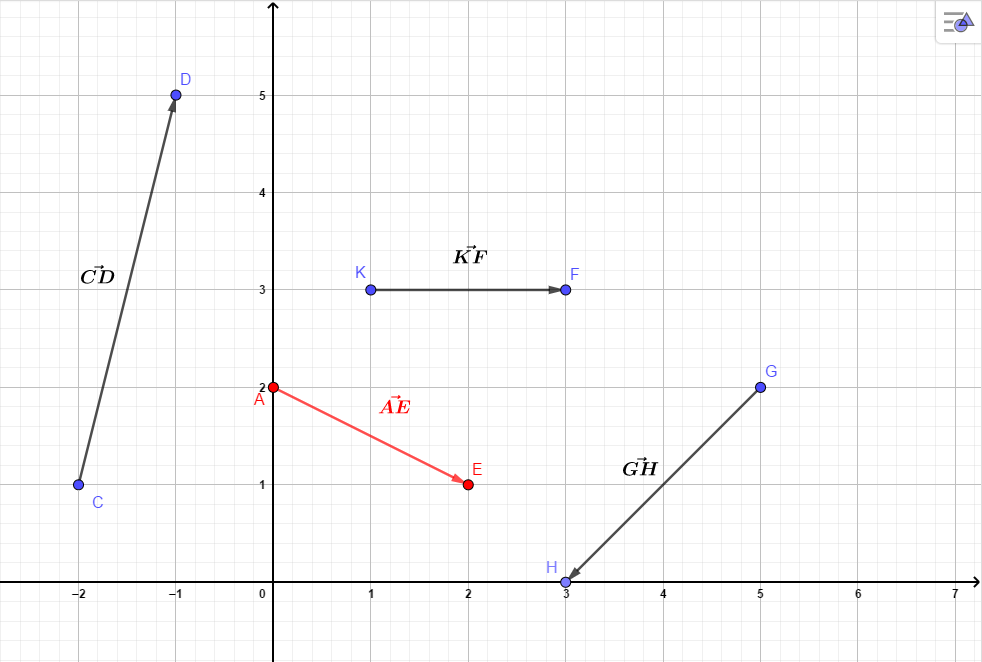
Beispiel: Der Pfeil beschreibt den Weg vom Punkt zum Punkt .
Bestimmen Sie die Koordinaten der Pfeile
Übung 2
- Verändern Sie die Anfangs- und Endpunkte der Pfeile und . Beobachten Sie die Veränderungen in den Koordinaten.
- Stellen Sie einen Pfeil dar, dessen -Koordinate negativ und dessen -Koordinate positiv ist.
- Stellen Sie einen Pfeil dar, dessen Koordinaten beide negativ sind.
- Beschreiben Sie, worin sich verschiedene Pfeile unterscheiden können.

Vektoren
Merke
Alle Pfeile, die gleich lang, parallel zueinander und gleich orientiert sind, gehören zur selben Verschiebung. Sie lassen sich somit durch den selben Vektor beschreiben.
Übung 3
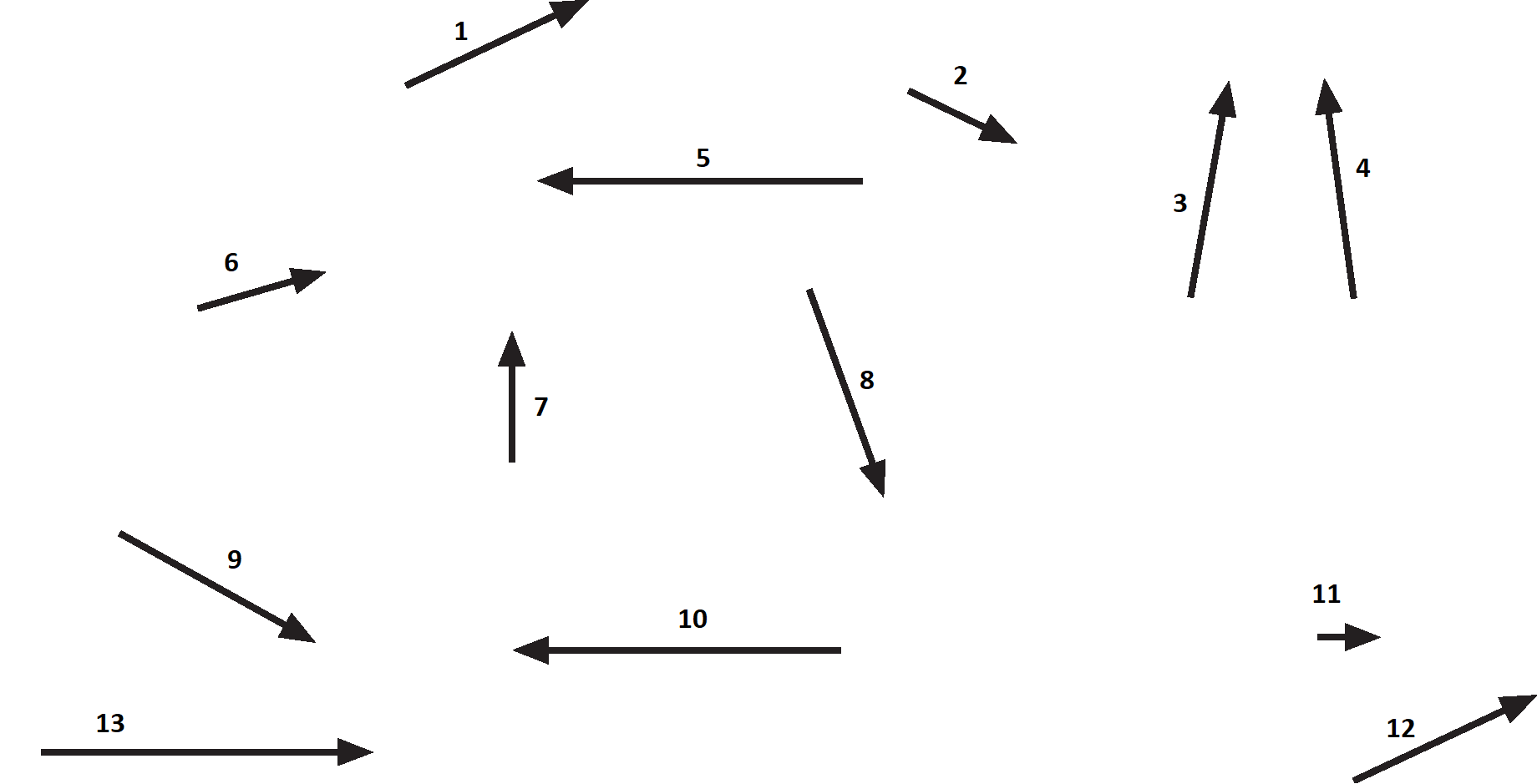
In der Abbildung sind unterschiedliche Pfeile dargestellt. Ordnen Sie jeweils zu:
- Pfeile, die zum selben Vektor gehören.
- Pfeile, die gleich lang sind, aber nicht zum selben Vektor gehören.
- Pfeile, die parallel sind, aber nicht zum selben Vektor gehören.
- Pfeile, die parallel, gleich lang, jedoch entgegengesetzt orientiert sind.
Übung 4
Sie sehen hier einen Pfeil. Er entspricht der grafischen Darstellung einer Verschiebung bzw. eines Vektors, dessen Koordinaten ebenfalls zu sehen sind.
- Lesen Sie mit Hilfe des Koordinatengitters die aktuellen Koordinaten des Anfangspunktes und des Endpunktes des Pfeiles ab. Nennen Sie dabei den Anfangspunkt am besten und den Endpunkt .
- Stellen Sie eine Vermutung über den Zusammenhang zwischen den Koordinaten des Anfangspunktes , des Endpunktes und des Vektors auf? Überprüfen Sie Ihre Vermutung für mindestens drei verschiedene Vektoren und notieren Sie Ihre Ergebnisse.
- Wie berechnet man die Koordinaten des Vektors, wenn Anfangs- und Endpunkt des Pfeiles allgemein gegeben sind: und ? Geben Sie eine Rechenvorschrift an.
- Geben Sie auch eine Rechenvorschrift für die Berechnung der Koordinaten eines Vektors im Raum an (Vektoren mit drei Einträgen).