Vektorrechnung/WHG Q1 Vermischte Übungen zu Vektoren: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 43: | Zeile 43: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
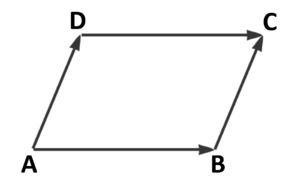
[[Datei:0 Abbildung 4.png| | [[Datei:0 Abbildung 4.png|mini|Abbildung 4]] | ||
Die Abbildung verdeutlich, dass es genügt zu überprüfen, ob <math>\vec{AB}=\vec{DC}</math> (bzw. <math>\vec{AD}=\vec{BC}</math>) gilt: | Die Abbildung verdeutlich, dass es genügt zu überprüfen, ob <math>\vec{AB}=\vec{DC}</math> (bzw. <math>\vec{AD}=\vec{BC}</math>) gilt: | ||
<math>\vec{AB}=\begin{pmatrix}4-2\\-1-3\\2-4\end{pmatrix}=\ begin{pmatrix}2\\-4\\-2\end{pmatrix}</math>; <math>\vec{DC}=\begin{pmatrix}3,25-1,25\\-0,3-3,7\\8-10\end{pmatrix}=\ begin{pmatrix}2\\-4\\-2\end{pmatrix}</math>; also gilt <math>\vec{AB}=\vec{DC}</math>. Folglich sind <math>A</math>, <math>B</math>, <math>C</math> und <math>D</math> die Ecken eines Parallelogramms. | <math>\vec{AB}=\begin{pmatrix}4-2\\-1-3\\2-4\end{pmatrix}=\begin{pmatrix}2\\-4\\-2\end{pmatrix}</math>; <math>\vec{DC}=\begin{pmatrix}3,25-1,25\\-0,3-3,7\\8-10\end{pmatrix}=\begin{pmatrix}2\\-4\\-2\end{pmatrix}</math>; also gilt <math>\vec{AB}=\vec{DC}</math>. Folglich sind <math>A</math>, <math>B</math>, <math>C</math> und <math>D</math> die Ecken eines Parallelogramms. | ||
}} | }} | ||
<br> | <br> | ||
Version vom 21. September 2020, 09:23 Uhr
Übung
Auf dieser Seite finden Sie vermischte Übungen zum Rechnen mit Vektoren.
Im Rahmen unterschiedlicher Aufgabentypen können Sie Ihr neu erworbenes Wissen vertiefen.
Ortsvektoren
Bestimmen Sie den Ortsvektor des Punktes , indem Sie Anfangs- und Endpunkt des Pfeiles bewegen.

Der Weg durch das Labyrinth - Vektoren zeichnen
- Zeichnen Sie mit Hilfe von Vektoren einen lückenlosen Weg durch das Labyrinth vom Start- zum Zielpunkt ein. Geben Sie dazu im Eingabefeld die Vektoren einzeln in folgender Schreibweise ein: Vektor((, ), (, )) Dies beschreibt den Vektor vom Punkt zum Punkt .
- Begründen Sie anschließend, welche der Pfeile zum selben Vektor gehören.

Vektoren im Koordinatensystem
Gegeben ist der Vektor .
- Zeichnen Sie drei Pfeile, die den Vektor repräsentieren, in ein Koordinatensystem.
- Es gilt: mit bestimmen Sie die Koordinaten von .
- Es gilt: mit bestimmen Sie die Koordinaten von .
- -
- Geht man von aus drei Einheiten in Richtung der -Achse und anschließend eine Einheit in Richtung der -Achse, so erreicht man : bzw. .
- Geht man von aus drei Einheiten in Richtung der -Achse und anschließend eine Einheit gegen die Richtung der -Achse, so erreicht man : bzw. .
Parallelogramm im Raum
Überprüfen Sie, ob die Punkte , , und die aufeinanderfolgenden Ecken eines Parallelogramms sind.
Die Abbildung verdeutlich, dass es genügt zu überprüfen, ob (bzw. ) gilt: ; ; also gilt . Folglich sind , , und die Ecken eines Parallelogramms.