Vektorrechnung/WHG Q1 Einstieg Vektoren: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 8: | Zeile 8: | ||
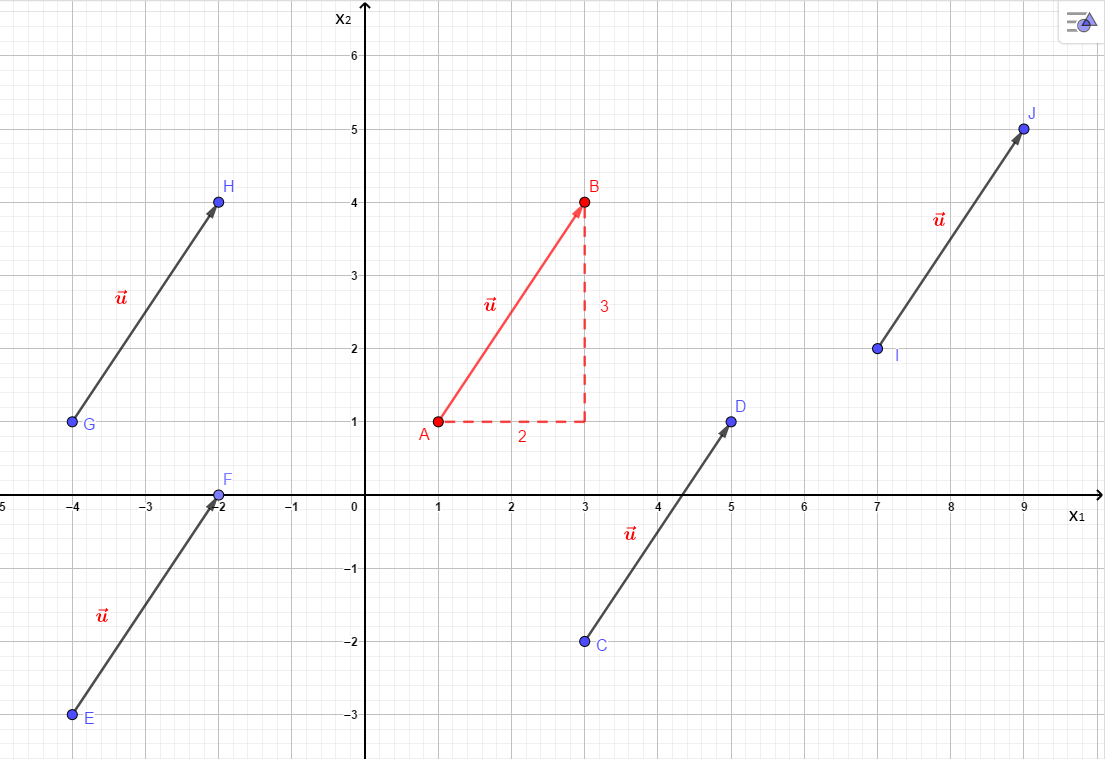
Die in der Abbildung eingezeichneten ''Pfeile'' repräsentieren alle die gleiche '''Verschiebung'''. Von einem beliebigen Ausgangspunkt lässt sich der zugehörige Endpunkt erreichen, indem man zwei Einheiten in Richtung der <math>x_1</math>-Achse und drei Einheiten in Richtung der <math>x_2</math>-Achse geht. | Die in der Abbildung eingezeichneten ''Pfeile'' repräsentieren alle die gleiche '''Verschiebung'''. Von einem beliebigen Ausgangspunkt lässt sich der zugehörige Endpunkt erreichen, indem man zwei Einheiten in Richtung der <math>x_1</math>-Achse und drei Einheiten in Richtung der <math>x_2</math>-Achse geht. | ||
Die Koordinaten einer solchen Verschiebung beschreibt man mit Hilfe eines '''Vektors (<math>\vec{u}</math>) | Die Koordinaten einer solchen Verschiebung beschreibt man mit Hilfe eines '''Vektors''' (<math>\vec{u}</math>): | ||
<math>\vec{u}=\begin{pmatrix}u_1\\u_2\end{pmatrix}=\begin{pmatrix}2\\3\end{pmatrix}</math>. | <math>\vec{u}=\begin{pmatrix}u_1\\u_2\end{pmatrix}=\begin{pmatrix}2\\3\end{pmatrix}</math>. | ||
Version vom 20. September 2020, 14:11 Uhr
Merke
Ein Pfeil ist ein geometrisches Objekt, das einen Anfangspunkt und einen Endpunkt besitzt.
Die in der Abbildung eingezeichneten Pfeile repräsentieren alle die gleiche Verschiebung. Von einem beliebigen Ausgangspunkt lässt sich der zugehörige Endpunkt erreichen, indem man zwei Einheiten in Richtung der -Achse und drei Einheiten in Richtung der -Achse geht.
Die Koordinaten einer solchen Verschiebung beschreibt man mit Hilfe eines Vektors (): .
Vektoren werden dabei als sogenannte Tupel dargestellt. Ein -Tupel ist eine Zusammenfassung von mathematischen Objekten in einer Liste .
