Vektorrechnung/WHG Q1 Einstieg Vektoren: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 2: | Zeile 2: | ||
{{2Spalten| | {{2Spalten| | ||
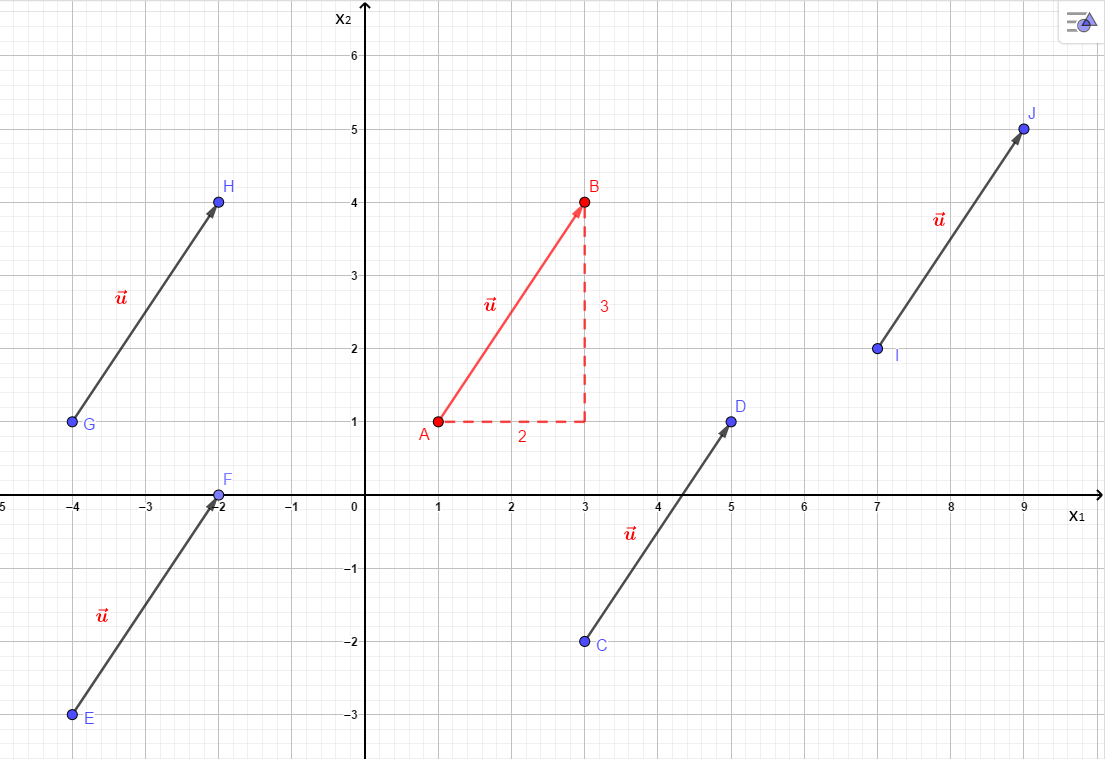
Die in der Abbildung eingezeichneten ''Pfeile'' repräsentieren alle die gleiche Verschiebung (<math>\vec{u}</math>). Von einem beliebigen Ausgangspunkt lässt sich der zugehörige Endpunkt erreichen, indem man zwei Einheiten in Richtung der <math>x_1</math>-Achse und drei Einheiten in Richtung der <math>x_2</math>-Achse geht. | Die in der Abbildung eingezeichneten ''Pfeile'' repräsentieren alle die gleiche Verschiebung (<math>\vec{u}</math>). Von einem beliebigen Ausgangspunkt lässt sich der zugehörige Endpunkt erreichen, indem man zwei Einheiten in Richtung der <math>x_1</math>-Achse und drei Einheiten in Richtung der <math>x_2</math>-Achse geht. | ||
Die Koordinaten einer solchen Verschiebung <math>\vec{u}</math> beschreibt man mit Hilfe eines Tupels: | |||
<math>\vec{u}=\begin{pmatrix}u_1\\u_2\end{pmatrix}=\begin{pmatrix}2\\3\end{pmatrix}</math> | |||
| | | | ||
[[Datei:0_Abbildung 1.png|200|center|Abbildung 1]] | [[Datei:0_Abbildung 1.png|200|center|Abbildung 1]] | ||
}} | }} | ||
{{Lösung versteckt| | |||
Ein <math>n</math>-Tupel ist eine Zusammenfassung von <math>n</math> mathematischen Objekten <math>x_1 ... x_n</math> in einer Liste. | |||
|Informationen anzeigen|Informationen verbergen}} | |||
<br> | <br> | ||
<br> | <br> | ||
{{Fortsetzung|weiter=Pfeile|weiterlink=WHG_Q1_Vektorrechnung/WHG_Q1_Pfeile|vorher=Übersicht|vorherlink=WHG Q1 Vektorrechnung/WHG Q1 Vektoren}} | {{Fortsetzung|weiter=Pfeile|weiterlink=WHG_Q1_Vektorrechnung/WHG_Q1_Pfeile|vorher=Übersicht|vorherlink=WHG Q1 Vektorrechnung/WHG Q1 Vektoren}} | ||
Version vom 20. September 2020, 13:54 Uhr
Die in der Abbildung eingezeichneten Pfeile repräsentieren alle die gleiche Verschiebung (). Von einem beliebigen Ausgangspunkt lässt sich der zugehörige Endpunkt erreichen, indem man zwei Einheiten in Richtung der -Achse und drei Einheiten in Richtung der -Achse geht.
Die Koordinaten einer solchen Verschiebung beschreibt man mit Hilfe eines Tupels:
Ein -Tupel ist eine Zusammenfassung von mathematischen Objekten in einer Liste.
