Lineare Funktionen im Aktiv-Urlaub: Unterschied zwischen den Versionen
K (Navigation geändert) |
K (1 Version importiert) |
Version vom 16. Mai 2020, 14:01 Uhr
Wir erarbeiten das Wissen für das Thema "Lineare Funktionen" mit Anwendungen aus dem Aktiv-Urlaub
Dazu beginnen wir mit einem Fitness-Test (das Vorwissen)
0) Vorwissen
Bearbeite die Aufgaben in der Tabelle: (Buch: Schnittpunkt Mathematik - Differenzierende Ausgabe 8)
| Du kannst | Übungen im Buch | Übungen online |
|---|---|---|
| -Koordinaten in ein Koordinatensystem
ablesen und eintragen |
S. 120 Nr. 1,2 |
|
| -aus Grafen Informationen ablesen und
passende Grafen zu Sachsituationen zeichen |
S. 120 Nr. 3,4 |
|
| -proportionale und umgekehrt proportionale Zuordnungen
erkennen und den Dreisatz anwenden |
S.120 Nr. 5 |
|
| -bei proportionalen und umgekehrt proportionalen
Zuordnungen den Dreisatz anwenden |
S.120 Nr. 6 |
|
Vergleiche deine Lösungen mit den Lösungen hinten im Buch!
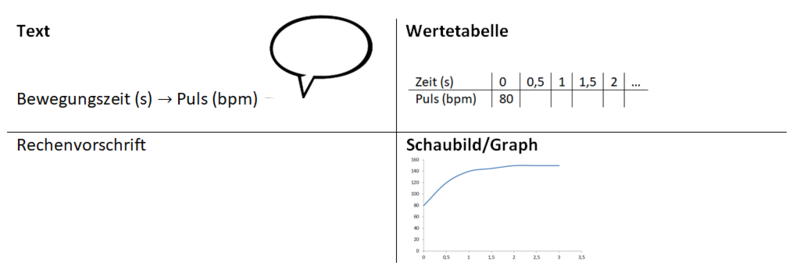
Um die '''Darstellungsformen''' von Zuordnungen zu wiederholen führe folgenden Fitnesstest durch.
Steige so schnell wie möglich auf einen Stuhl hoch und wieder herunter. Dauer: 1 Minute. Danach miss 15 Sekunden lang deinen Puls und notiere den Wert in der Tabelle.
Tipp zur Pulsmessung: 15 Sekunden messen, diesen Wert mit 4 multiplizieren ergibt dann die Schläge pro Minute ("beats per Minute bpm)
| Zeit
in Minuten |
0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
|---|---|---|---|---|---|---|---|
| Puls
in bpm |
a) Stelle deine Ergebnisse nun in einem Schaubild dar.
b) Darfst du die einzelnen Punkte zu einer Linie verbinden?
c) Beschreibe den Verlauf des Graphen.Zusammenfassung:
Nun hast du die Darstellungsformen von Zuordnungen wiederholt.
Jetzt bist du fit für den Aktivurlaub:
Die mathematische Inhalte werden in der folgenden Reihenfolgen erarbeitet:
1) Zuordnungen und Funktionen
2) Lineare Funktionen