Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Flächen und Volumina/Flächen: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Markierung: Quelltext-Bearbeitung 2017 |
(Merksatz hinzugefügt, Graphiken ergänzt) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 2: | Zeile 2: | ||
}} | }} | ||
== Erste Erkundungen == | ==Erste Erkundungen== | ||
{{Box|Erkundung|Auf dem Bild siehst du verschiedene Verpackungen, die näherungsweise Prismen darstellen. Sammle Ideen, wie du den Materialverbrauch, d.h. die Fläche an verbrauchtem Pappkarton bestimmen kannst. Notiere deine Ideen im Heft und erstelle eine Skizze.|Unterrichtsidee | {{Box|Erkundung|Auf dem Bild siehst du verschiedene Verpackungen, die näherungsweise Prismen darstellen. Sammle Ideen, wie du den Materialverbrauch, d.h. die Fläche an verbrauchtem Pappkarton bestimmen kannst. Notiere deine Ideen im Heft und erstelle eine Skizze.|Unterrichtsidee | ||
}} | }} | ||
== Oberfläche und Körpernetze == | ==Oberfläche und Körpernetze== | ||
[[Datei:Prismen.png|800px]] | |||
<br /> | |||
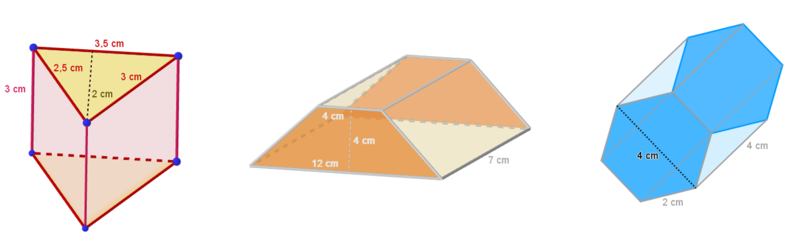
{{Box|Aufgabe 1a|# Wähle einen der auf dem Bild dargestellten Gegenstände aus. | {{Box|Aufgabe 1a|# Wähle einen der auf dem Bild dargestellten Gegenstände aus. | ||
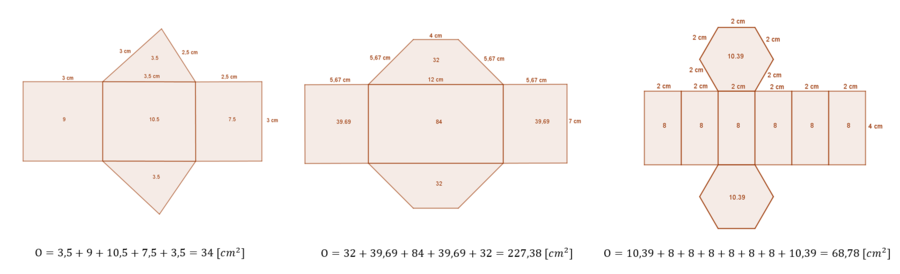
# Zeichne ein Körpernetz zu dem von dir ausgewählten Prisma. Beschreibe, in welche Teilflächen sich die Oberfläche des Körpers zerlegen lässt. | # Zeichne ein Körpernetz zu dem von dir ausgewählten Prisma. Beschreibe, in welche Teilflächen sich die Oberfläche des Körpers zerlegen lässt. Überprüfe deine Zeichnung mithilfe des folgenden Applets. | ||
# Berechne den Flächeninhalt der Oberfläche, indem du den Flächeninhalt der Teilflächen berechnest und die Ergebnisse addierts. | # Berechne den Flächeninhalt der Oberfläche, indem du den Flächeninhalt der Teilflächen berechnest und die Ergebnisse addierts. | ||
Wiederhole das Vorgehen für die anderen beiden Prismen.|Übung | Wiederhole das Vorgehen für die anderen beiden Prismen.|Übung | ||
}} | }} | ||
{{Lösung versteckt| | |||
'''Hinweise zum Applet''' | |||
#Klicke einmal auf das Applet. Oben links in der Ecke erscheinen verschiedene Werkzeuge. | |||
#Zeichne als erstes die Grundfläche mit dem Vielecks-Werkzeug (zweites Symbol von links). Setze dazu die gewünschte Anzahl an Eckpunkten. Die Eckpunkte verbinden sich automatisch. | |||
#Um aus dem Vieleck ein Prisma zu konstruieren, klicke das Prismen-Werkzeug (drittes Symbol von links) und dann dein Vieleck an. Gib die gewünschte Höhe an. | |||
#Mit dem Mauszeiger (erstes Symbol von lins) kannst du die Punkt der Grundfläche verschieben und schauen, wie sich das Prisma verändert. Über den Button "Drehen" kannst du dir das Prisma aus verschiedenen Perspektiven ansehen. | |||
#Um das Körpernetz deines Prismas angezeigt zu bekommen, klicke auf das Prisma-Werkzeug. Hier kannst du die Option "Netz" auswählen. Klicke erst "Netz" und dann dein Prisma an. | |||
#Willst du ein neues Prisma zeichnen, kannst du das alte mit dem Mülleimer-Symbol löschen. | |||
Sollte das Applet nicht richtig laden, klicke [https://www.geogebra.org/m/PHtUWdJ8]. | Sollte das Applet nicht richtig laden, klicke [https://www.geogebra.org/m/PHtUWdJ8]. | ||
<ggb_applet id="PHtUWdJ8" width="900" height="600" /> | <ggb_applet id="PHtUWdJ8" width="900" height="600" /> | ||
Applet anzeigen|Applet verbergen}} | |||
{{Lösung versteckt| | {{Lösung versteckt|[[Datei:Prismennetze.png|900px]]|Lösung anzeigen|Lösung verbergen}} | ||
{{Box|Aufgabe 1b|Beschreibe, welche Gemeinsamkeiten und Unterschiede bei den Prismen auftreten. Kannst du ein allgemeines Vorgehen erkennen? Notiere deine Beobachtungen im Heft|Übung | {{Box|Aufgabe 1b|Beschreibe, welche Gemeinsamkeiten und Unterschiede bei den Prismen auftreten. Kannst du ein allgemeines Vorgehen erkennen? Notiere deine Beobachtungen im Heft|Übung | ||
}} | }} | ||
== Oberfläche von Prismen == | ==Oberfläche von Prismen== | ||
<span style="color:" blue> Joana </span> und <span style="color:" orange> Hendrik </span> reflektieren ihr Vorgehen bei der vorhergehenden Aufgabe. | |||
[[Datei:Oberfläche Prisma Gespräch.png|700px]] | |||
{{Box|Aufgabe 2|Erkläre mithilfe der von dir in Aufgabe 1 gezeichneten Körpernetze, wie die einzelnen Seitenflächen zusammen gefasst werden können. Stelle eine Formel auf, mit der sich der Flächeninhalt der Mantelfläche (d.h. aller Seitenflächen)in einem beliebigen Prisma berechnen lässt.|Übung}} | |||
{{Lösung versteckt| Die Lösungen zu Aufgabe 1 zeigen, dass sich die einzelnen Seitenflächen zu einem großen Rechteck zusammenfügen lasssen. Was ist die Länge und was ist die Breite dieses Rechtecks? |Tipp 1 anzeigen|Tipp verbergen}} | |||
{{Lösung versteckt| Der Umfang der Grundfläche ist bei der Beantwortung der Frage hilfreich. |Tipp 2 anzeigen|Tipp verbergen}} | |||
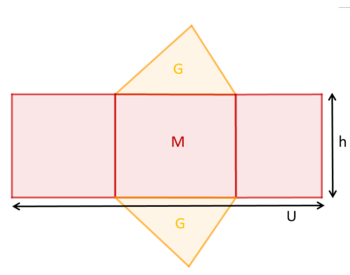
{{Box|Merke|Die '''Oberfläche eines Prismas''' besteht aus zweimal der gleichen '''Grundfläche''' und einem '''Mantel'''. Der Mantel setzt sich aus allen Seitenflächen des Prismas zusammen. Für den Oberflächeninhalt gilt also | |||
<blockquote><math> O=2 \cdot G + M </math> </blockquote>. | |||
Damit der Mantel auf die Grundfläche passt, muss die Mantelfläche genauso lang sein wie der Umfang der Grundfläche. Also gilt | |||
<blockquote><math> M= U \cdot h </math> </blockquote>. [[Datei:Oberfläche Prisma.png|350px]]|Merksatz}} | |||
Version vom 27. März 2020, 18:12 Uhr
Info
Überall im Alltag begegnen uns verschiedene Verpackungen. Welche Verpackung verbraucht am meisten Material? Welche schont die Umwelt? Die Oberfläche eines Quaders oder eines Würfels kannst du bereits bestimmen. Auf dieser Seite erkundest du, wie man die Fläche von anderen Prismen sowie Zylindern berechnet.
Erste Erkundungen
Erkundung
Auf dem Bild siehst du verschiedene Verpackungen, die näherungsweise Prismen darstellen. Sammle Ideen, wie du den Materialverbrauch, d.h. die Fläche an verbrauchtem Pappkarton bestimmen kannst. Notiere deine Ideen im Heft und erstelle eine Skizze.
Oberfläche und Körpernetze
Aufgabe 1a
- Wähle einen der auf dem Bild dargestellten Gegenstände aus.
- Zeichne ein Körpernetz zu dem von dir ausgewählten Prisma. Beschreibe, in welche Teilflächen sich die Oberfläche des Körpers zerlegen lässt. Überprüfe deine Zeichnung mithilfe des folgenden Applets.
- Berechne den Flächeninhalt der Oberfläche, indem du den Flächeninhalt der Teilflächen berechnest und die Ergebnisse addierts.
Hinweise zum Applet
- Klicke einmal auf das Applet. Oben links in der Ecke erscheinen verschiedene Werkzeuge.
- Zeichne als erstes die Grundfläche mit dem Vielecks-Werkzeug (zweites Symbol von links). Setze dazu die gewünschte Anzahl an Eckpunkten. Die Eckpunkte verbinden sich automatisch.
- Um aus dem Vieleck ein Prisma zu konstruieren, klicke das Prismen-Werkzeug (drittes Symbol von links) und dann dein Vieleck an. Gib die gewünschte Höhe an.
- Mit dem Mauszeiger (erstes Symbol von lins) kannst du die Punkt der Grundfläche verschieben und schauen, wie sich das Prisma verändert. Über den Button "Drehen" kannst du dir das Prisma aus verschiedenen Perspektiven ansehen.
- Um das Körpernetz deines Prismas angezeigt zu bekommen, klicke auf das Prisma-Werkzeug. Hier kannst du die Option "Netz" auswählen. Klicke erst "Netz" und dann dein Prisma an.
- Willst du ein neues Prisma zeichnen, kannst du das alte mit dem Mülleimer-Symbol löschen.
Sollte das Applet nicht richtig laden, klicke [1].

Aufgabe 1b
Beschreibe, welche Gemeinsamkeiten und Unterschiede bei den Prismen auftreten. Kannst du ein allgemeines Vorgehen erkennen? Notiere deine Beobachtungen im Heft
Oberfläche von Prismen
Joana und Hendrik reflektieren ihr Vorgehen bei der vorhergehenden Aufgabe.

Aufgabe 2
Erkläre mithilfe der von dir in Aufgabe 1 gezeichneten Körpernetze, wie die einzelnen Seitenflächen zusammen gefasst werden können. Stelle eine Formel auf, mit der sich der Flächeninhalt der Mantelfläche (d.h. aller Seitenflächen)in einem beliebigen Prisma berechnen lässt.
Die Lösungen zu Aufgabe 1 zeigen, dass sich die einzelnen Seitenflächen zu einem großen Rechteck zusammenfügen lasssen. Was ist die Länge und was ist die Breite dieses Rechtecks?
Der Umfang der Grundfläche ist bei der Beantwortung der Frage hilfreich.
Merke
Die Oberfläche eines Prismas besteht aus zweimal der gleichen Grundfläche und einem Mantel. Der Mantel setzt sich aus allen Seitenflächen des Prismas zusammen. Für den Oberflächeninhalt gilt also
.
Damit der Mantel auf die Grundfläche passt, muss die Mantelfläche genauso lang sein wie der Umfang der Grundfläche. Also gilt
.