Einführung von Funktionen: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
K (Andrea Schellmann verschob die Seite Einführung von Funktionen nach Benutzer:Agnes lint/Einführung von Funktionen: Lernpfad im Aufbau) |
Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken|{{Einführung in die Funktionen}}}} | {{Navigation verstecken|{{Einführung in die Funktionen}}}} | ||
__NOTOC__ | __NOTOC__ | ||
{{Box|Lernpfad|Einführung von Funktionen|Lernpfad}} | |||
= Einführung von Funktionen = | |||
Im Rahmen dieses Lernpfades solltes du gewisse Lernziele und Grundkompetenzen für die schriftliche Reifeprüfung erwerben. | |||
{{Lösung versteckt|Verschiedene Darstellungsarten von Zusammenhänge kennen, anwenden und interpretieren können. |Lernziele |Lernziele}} | |||
{{Lösung versteckt|* FA 1.3: Zwischen tabellarischer und graphischer Darstellung von Funktionen wechseln können | |||
* FA 1.4: Aus Tabellen, Graphen und Gleichungen von Funktionen Werte(paare) ermitteln und im Kontext deuten können |Grundkompetenzen |Grundkompetenzen}} | |||
==='''Funktionen''' – was ist das eigentlich genau?=== | ==='''Funktionen''' – was ist das eigentlich genau?=== | ||
Wir Menschen erkennen und suchen in unserer Welt seit jeher | {{Box|Info|Wir Menschen erkennen und suchen in unserer Welt seit jeher nach Zusammenhängen und versuchen Verbindungen zwischen unterschiedlichsten Ereignissen herzustellen. | ||
So kann etwa ein Zusammenhang wischen der Körpergröße und dem Körpergewicht festgestellt werden. Die Körpergröße ist dabei ursächlich für das Körpergewicht. Im folgenden Lernpfad wirst du erfahren, wie man Zusammenhänge mit sogenannten Funktionen genau beschreiben und graphisch sichtbar machen kann.|Kurzinfo}} | |||
Im folgenden Lernpfad wirst du erfahren, wie man Zusammenhänge mit Funktionen | |||
=== Einführung des Funktionsbegriff === | |||
Um den vorher bereits besprochenen Zusammenhang zwischen Körpergröße und Gewicht untersuchen zu können, müssen wir zu allererst eine Wertetabelle erstellen. Dabei wird in der ersten Spalte die Körpergröße und in die zweite Spalte das Gewicht eingetragen. | |||
{{Box|Wertetabelle|Eine Tabelle, die eine Zuordnung darstellt, nennt man Wertetabelle. | |||
* In der ersten Spalte stehen die Werte der unabhängigen Größe, in der zweiten die der abhängigen. | |||
* Die Einheiten der Größen sollen ebenso angegeben sein. |Merksatz}} | |||
:::{| class="wikitable float left" | :::{| class="wikitable float left" | ||
|- style="background-color:#FFFFFF" | |- style="background-color:#FFFFFF" | ||
! style="width:7em" |Körpergröße!! style="width:7em" |Gewicht | ! style="width:7em" |Körpergröße (in cm)!! style="width:7em" |Gewicht (in kg) | ||
|- | |- | ||
| style="text-align:center" |154 | | style="text-align:center" |154 || style="text-align:center" |51 | ||
|- | |- | ||
| style="text-align:center" |158 | | style="text-align:center" |158 || style="text-align:center" |58 | ||
|- | |- | ||
| style="text-align:center" |161 | | style="text-align:center" |161 || style="text-align:center" |57 | ||
|- | |- | ||
| style="text-align:center" |172 | | style="text-align:center" |172 || style="text-align:center" |65 | ||
|- | |- | ||
| style="text-align:center" |178 | | style="text-align:center" |178 || style="text-align:center" |70 | ||
|- | |- | ||
| style="text-align:center" |183 | | style="text-align:center" |183 || style="text-align:center" |78 | ||
|- | |- | ||
| style="text-align:center" |187 | | style="text-align:center" |187 || style="text-align:center" |90 | ||
|- | |- | ||
| style="text-align:center" |193 | | style="text-align:center" |193 || style="text-align:center" |89 | ||
|} | |} | ||
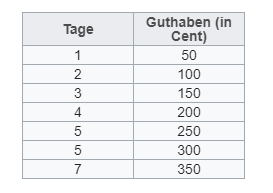
Um | {{Box|Üben|Versuche nun selbst in deinem Heft eine Wertetabelle zu folgenden Angaben zu erstellen. Max spart ab heute eine Woche lang jeden Tag 50 Cent. Jedem Tag wird Max' Guthaben zugeordnet. |Üben}} | ||
[[Datei: | |||
{{Box|Lösung|{{Lösung versteckt|[[Datei:Lösung Tabelle Max.png|rahmenlos|Lösung Wertetabelle Max]] |Lösung zeigen|Lösung verstecken}}|Lösung}} | |||
{{Box|Graph einer Zuordnung|Um den Graphen einer Zuordnung zu erhalten, werden Wertepaare in ein Koordinatensystem eingezeichnet. | |||
* Die unabhängige Variable wird auf die waagrechte Achse (Abszisse) eingetragen, die abhängige Größe in Richtung der senkrechten Achse (Ordinate). | |||
* Die Beschriftung der Achsen ist bei jedem Graphen sehr wichtig. Es muss ersichtlich sein welche Werte auf den einzelnen Achsen aufgetragen werden und in welcher Einheit sie aufgetragen werden. |Merksatz}} | |||
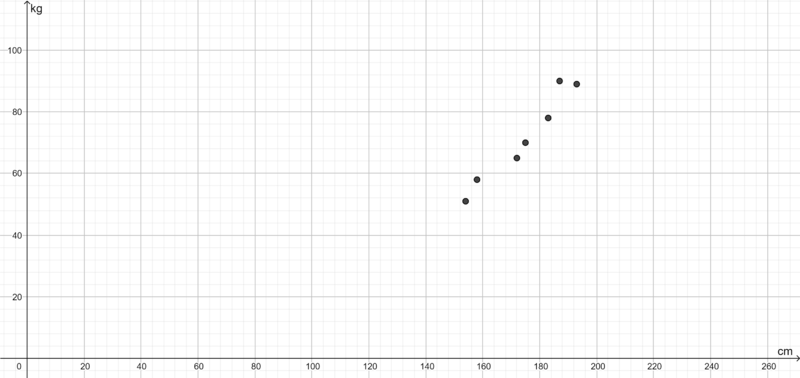
Um den Zusammenhang zwischen Körpergröße und Körpergewicht graphisch sichtbar zu machen, werden die Wertepaare nun in ein Koordinatensystem eingetragen. | |||
[[Datei:Eingetragene Wertepaare im Koordinatensystem.png|rahmenlos|800px]] | |||
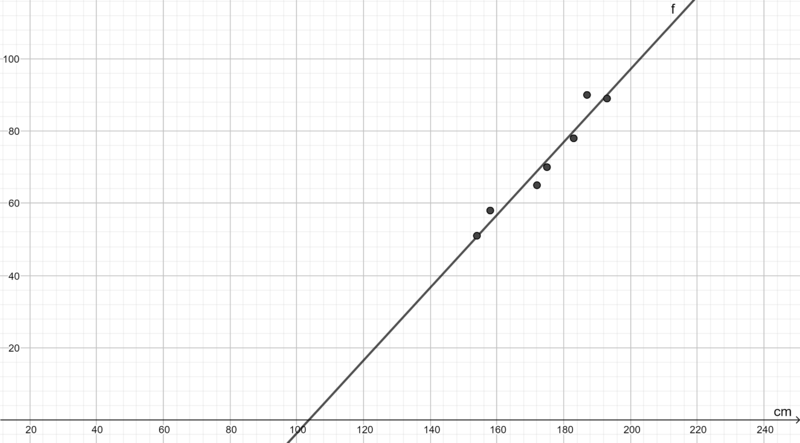
Man erkennt nun, dass die Wertepaare zumindest annähernd auf einer geraden Linie liegen. Natürlich berührt die Linie nicht alle Punkt, allerdings erhält man so eine sogenannte Annäherung. | |||
[[Datei:Geogebra-export (2).png|rahmenlos|800px]] | |||
Die gerade Linie ergibt also für jeden beliebigen x-Wert einen zugehörigen y-Wert (nicht nur für unsere bereits eingetragenen Punkte.) | |||
{{Box|Info|Graph und Wertetabelle können nicht immer alle möglichen Wertepaare eines Zusammenhangsdarstellen. Durch die durchgezogene Linie stellt der Graph jedoch alle unendlich vielen Wertepaare dar. Dies würde natürlich mit einer Wertetabelle nie gelingen. |Kurzinfo}} | |||
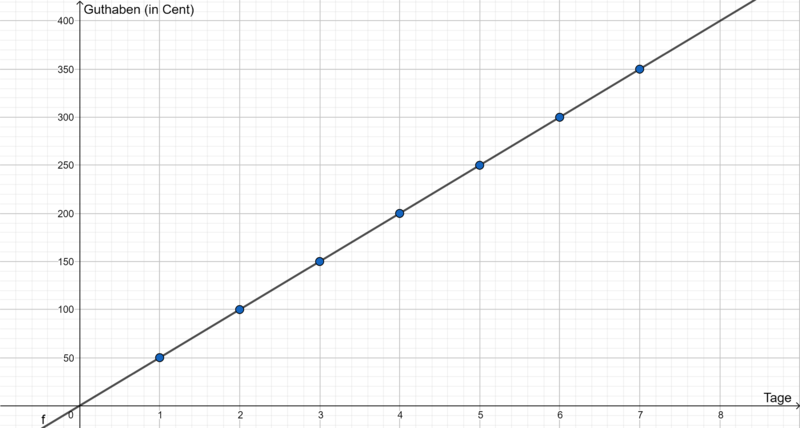
{{Box|Üben|Versuche nun in deinem Heft die Wertepaare vom Guthaben von Max in ein Koordinatensystem eintragen und leg eine passende Linie durch die Wertepaare. |Üben}} | |||
{{Box|Lösung|{{Lösung versteckt|[[Datei:Lineare Funktion Max Guthaben.png|rahmenlos|800px]] |Lösung zeigen|Lösung verstecken}}|Lösung}} | |||
{{Box|Termdarstellung|Die Termdarstellung drückt den Zusammenhang zwischen zwei Größen in Form einer Gleichung aus. Für diese Darstellungsart ist es unbedingt notwendig, die einzelnen Größen des Zusammenhangs durch Buchstaben zu benennen und mit den dazugehörigen Einheiten klar auszuweisen. | |||
Die Schreibweise f(x) (gesprochen "f von x") drückt aus, dass die Größe f von der unabhängigen Größe x abhängt.|Merksatz}} | |||
===Nun sollst du das Erstellen von Wertetabellen und das Erstellen von Funktionen durch Wertepaare im Koordinatensystem üben.=== | |||
<div class="box arbeitsmethode"> | |||
==Aufgabe 1== | |||
'''Für diese Aufgabe benötigst du dein Heft!''' [[Datei:Notepad-117597.svg|32x32px]]. | |||
In der folgenden Tabelle sind die Besucherzahlen eines Freibades während einer Woche dargestellt. 1 = Montag, 2 = Dienstag, 3 = Mittwoch... | |||
'''a)''' Übernimm die Werte aus der Tabelle in dein Heft | |||
'''b)''' Zeichne den zugehörigen Graphen in ein Koordinatensystem. Zeichne einen Graphen der jeden Punkt berührt. | |||
{| class="wikitable" | |||
|- style="background-color:#FFFFFF" | |||
! style="width:7em" |Wochentag!! style="width:7em" |Besucheranzahl | |||
|- | |||
| style="text-align:center" |1|| style="text-align:center" |340 | |||
|- | |||
| style="text-align:center" |2|| style="text-align:center" |430 | |||
|- | |||
| style="text-align:center" |3|| style="text-align:center" |412 | |||
|- | |||
| style="text-align:center" |4|| style="text-align:center" |680 | |||
|- | |||
| style="text-align:center" |5|| style="text-align:center" |25 | |||
|- | |||
| style="text-align:center" |6|| style="text-align:center" |55 | |||
|- | |||
| style="text-align:center" |7|| style="text-align:center" |578 | |||
|} | |||
Dein Helfer Ben der Pinguin hat die Aufgabe 1 auch erledigt. Vergleiche deine Lösung mit ihm! | |||
[[Datei:Penguin-158551.png|rahmenlos|32x32px]] | |||
{{Lösung versteckt| | |||
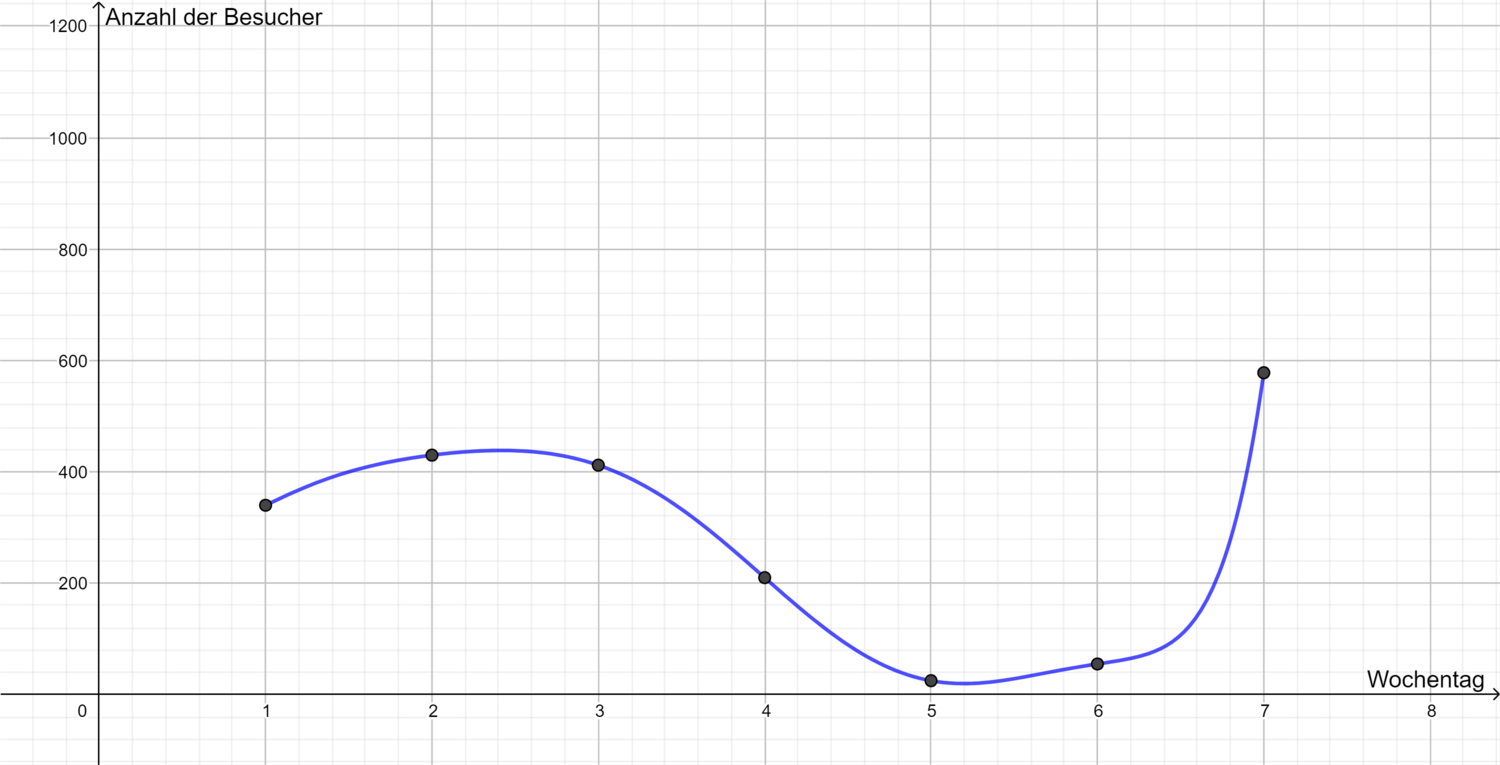
[[Datei:Kurve Aufgabe 1 Agnes.png|rahmenlos|1500px|Lösungen]]|Lösungen von Ben anzeigen|Lösungen verbergen}} | |||
</div> | |||
===Nun sollst du das Erstellen von Wertetabellen und das Erstellen von Funktionen durch Wertepaare im Koordinatensystem üben.=== | ===Nun sollst du das Erstellen von Wertetabellen und das Erstellen von Funktionen durch Wertepaare im Koordinatensystem üben.=== | ||
Version vom 26. März 2020, 09:17 Uhr
Lernpfad
Einführung von Funktionen
Einführung von Funktionen
Im Rahmen dieses Lernpfades solltes du gewisse Lernziele und Grundkompetenzen für die schriftliche Reifeprüfung erwerben.
Verschiedene Darstellungsarten von Zusammenhänge kennen, anwenden und interpretieren können.
- FA 1.3: Zwischen tabellarischer und graphischer Darstellung von Funktionen wechseln können
- FA 1.4: Aus Tabellen, Graphen und Gleichungen von Funktionen Werte(paare) ermitteln und im Kontext deuten können
Funktionen – was ist das eigentlich genau?
Info
Wir Menschen erkennen und suchen in unserer Welt seit jeher nach Zusammenhängen und versuchen Verbindungen zwischen unterschiedlichsten Ereignissen herzustellen.
So kann etwa ein Zusammenhang wischen der Körpergröße und dem Körpergewicht festgestellt werden. Die Körpergröße ist dabei ursächlich für das Körpergewicht. Im folgenden Lernpfad wirst du erfahren, wie man Zusammenhänge mit sogenannten Funktionen genau beschreiben und graphisch sichtbar machen kann.
Einführung des Funktionsbegriff
Um den vorher bereits besprochenen Zusammenhang zwischen Körpergröße und Gewicht untersuchen zu können, müssen wir zu allererst eine Wertetabelle erstellen. Dabei wird in der ersten Spalte die Körpergröße und in die zweite Spalte das Gewicht eingetragen.
Wertetabelle
Eine Tabelle, die eine Zuordnung darstellt, nennt man Wertetabelle.
- In der ersten Spalte stehen die Werte der unabhängigen Größe, in der zweiten die der abhängigen.
- Die Einheiten der Größen sollen ebenso angegeben sein.
Körpergröße (in cm) Gewicht (in kg) 154 51 158 58 161 57 172 65 178 70 183 78 187 90 193 89
Üben
Versuche nun selbst in deinem Heft eine Wertetabelle zu folgenden Angaben zu erstellen. Max spart ab heute eine Woche lang jeden Tag 50 Cent. Jedem Tag wird Max' Guthaben zugeordnet.
Lösung
Graph einer Zuordnung
Um den Graphen einer Zuordnung zu erhalten, werden Wertepaare in ein Koordinatensystem eingezeichnet.
- Die unabhängige Variable wird auf die waagrechte Achse (Abszisse) eingetragen, die abhängige Größe in Richtung der senkrechten Achse (Ordinate).
- Die Beschriftung der Achsen ist bei jedem Graphen sehr wichtig. Es muss ersichtlich sein welche Werte auf den einzelnen Achsen aufgetragen werden und in welcher Einheit sie aufgetragen werden.
Um den Zusammenhang zwischen Körpergröße und Körpergewicht graphisch sichtbar zu machen, werden die Wertepaare nun in ein Koordinatensystem eingetragen.
Man erkennt nun, dass die Wertepaare zumindest annähernd auf einer geraden Linie liegen. Natürlich berührt die Linie nicht alle Punkt, allerdings erhält man so eine sogenannte Annäherung.
.png)
Die gerade Linie ergibt also für jeden beliebigen x-Wert einen zugehörigen y-Wert (nicht nur für unsere bereits eingetragenen Punkte.)
Info
Graph und Wertetabelle können nicht immer alle möglichen Wertepaare eines Zusammenhangsdarstellen. Durch die durchgezogene Linie stellt der Graph jedoch alle unendlich vielen Wertepaare dar. Dies würde natürlich mit einer Wertetabelle nie gelingen.
Üben
Versuche nun in deinem Heft die Wertepaare vom Guthaben von Max in ein Koordinatensystem eintragen und leg eine passende Linie durch die Wertepaare.
Lösung
Termdarstellung
Die Termdarstellung drückt den Zusammenhang zwischen zwei Größen in Form einer Gleichung aus. Für diese Darstellungsart ist es unbedingt notwendig, die einzelnen Größen des Zusammenhangs durch Buchstaben zu benennen und mit den dazugehörigen Einheiten klar auszuweisen.
Die Schreibweise f(x) (gesprochen "f von x") drückt aus, dass die Größe f von der unabhängigen Größe x abhängt.Nun sollst du das Erstellen von Wertetabellen und das Erstellen von Funktionen durch Wertepaare im Koordinatensystem üben.
Aufgabe 1
Für diese Aufgabe benötigst du dein Heft! 
.
In der folgenden Tabelle sind die Besucherzahlen eines Freibades während einer Woche dargestellt. 1 = Montag, 2 = Dienstag, 3 = Mittwoch...
a) Übernimm die Werte aus der Tabelle in dein Heft
b) Zeichne den zugehörigen Graphen in ein Koordinatensystem. Zeichne einen Graphen der jeden Punkt berührt.
| Wochentag | Besucheranzahl |
|---|---|
| 1 | 340 |
| 2 | 430 |
| 3 | 412 |
| 4 | 680 |
| 5 | 25 |
| 6 | 55 |
| 7 | 578 |
Dein Helfer Ben der Pinguin hat die Aufgabe 1 auch erledigt. Vergleiche deine Lösung mit ihm!
Nun sollst du das Erstellen von Wertetabellen und das Erstellen von Funktionen durch Wertepaare im Koordinatensystem üben.
Aufgabe 1
Für diese Aufgabe benötigst du dein Heft! .
In der folgenden Tabelle sind die Besucherzahlen eines Freibades während einer Woche dargestellt. 1 = Montag, 2 = Dienstag, 3 = Mittwoch... a) Übernimm die Werte aus der Tabelle in dein Heft b) Zeichne den zugehörigen Graphen in ein Koordinatensystem. Zeichne einen Graphen der jeden Punkt berührt.
| Wochentag | Besucheranzahl |
|---|---|
| 1 | 340 |
| 2 | 430 |
| 3 | 412 |
| 4 | 680 |
| 5 | 25 |
| 6 | 55 |
| 7 | 578 |
Dein Helfer Ben der Pinguin hat die Aufgabe 1 auch erledigt. Vergleiche deine Lösung mit ihm!
Aufgabe 2
Schau dir das Video an und erkläre die Begriffe Definitionsmenge und Wertemenge.
Aufgabe 3
Merke!
Funktionen sind Zuordnungen mit einer besonderen Eigenschaft: Als Funktion bezeichnet man eine Zuordnung, die jedem Argument genau einen Wert, den Funktionswert, zuordnet. Vereinfacht gesagt:" Eine Funktion ist eine eindeutige Zuordnung."
