Einführung von Funktionen: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „{{Navigation verstecken|{{Einführung in die Funktionen}}}} __NOTOC__ ==='''Funktionen''' – was ist das eigentlich genau?=== Wir Menschen erkennen und suchen…“) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| Zeile 83: | Zeile 83: | ||
Funktionen sind Zuordnungen mit einer besonderen Eigenschaft: Als Funktion bezeichnet man eine Zuordnung, die jedem Argument genau einen Wert, den Funktionswert, zuordnet. Vereinfacht gesagt:" Eine Funktion ist eine eindeutige Zuordnung." | Funktionen sind Zuordnungen mit einer besonderen Eigenschaft: Als Funktion bezeichnet man eine Zuordnung, die jedem Argument genau einen Wert, den Funktionswert, zuordnet. Vereinfacht gesagt:" Eine Funktion ist eine eindeutige Zuordnung." | ||
Version vom 25. März 2020, 11:41 Uhr
Funktionen – was ist das eigentlich genau?
Wir Menschen erkennen und suchen in unserer Welt seit jeher Zusammenhänge. Beispiele dafür sind: Der Zusammenhang zwischen zwei Größen wird gesucht, auch wenn die beiden Größen nicht ursächlich für einander sind. So kann etwa ein Zusammenhang wischen der Körpergröße und dem Körpergewicht festgestellt werden. Die Körpergröße ist natürlich ursächlich für das Körpergewicht. Im folgenden Lernpfad wirst du erfahren, wie man Zusammenhänge mit Funktionen sehr genau beschreiben und erstellen kann.
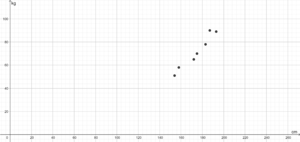
Um den Zusammenhang zwischen Körpergröße und Gewicht untersuchen zu können, müssen wir zu allererst eine Wertetabelle erstellen:
Körpergröße Gewicht 154 cm 51 kg 158 cm 58 kg 161 cm 57 kg 172 cm 65 kg 178 cm 70 kg 183 cm 78 kg 187 cm 90 kg 193 cm 89 kg
Um nun die Funktion sichtbar zu machen können wir die Wertepaare in ein Koordinatensystem eintragen.
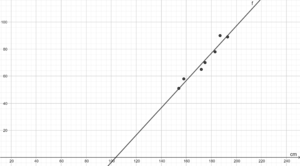
Um den Graphen einer Zuordnung zu erhalten, wird nach dem Eintragen der Wertepaare ein Graph durch die Punkte gelegt. Eine Funktion kann auch nur eine Annäherung an die Wertepaare sein. In unserem Beispiel sieht man, dass man eine gerade durchlegen kann und somit eine Annäherung erhält.
Nun sollst du das Erstellen von Wertetabellen und das Erstellen von Funktionen durch Wertepaare im Koordinatensystem üben.
Aufgabe 1
Für diese Aufgabe benötigst du dein Heft! ![]() .
.
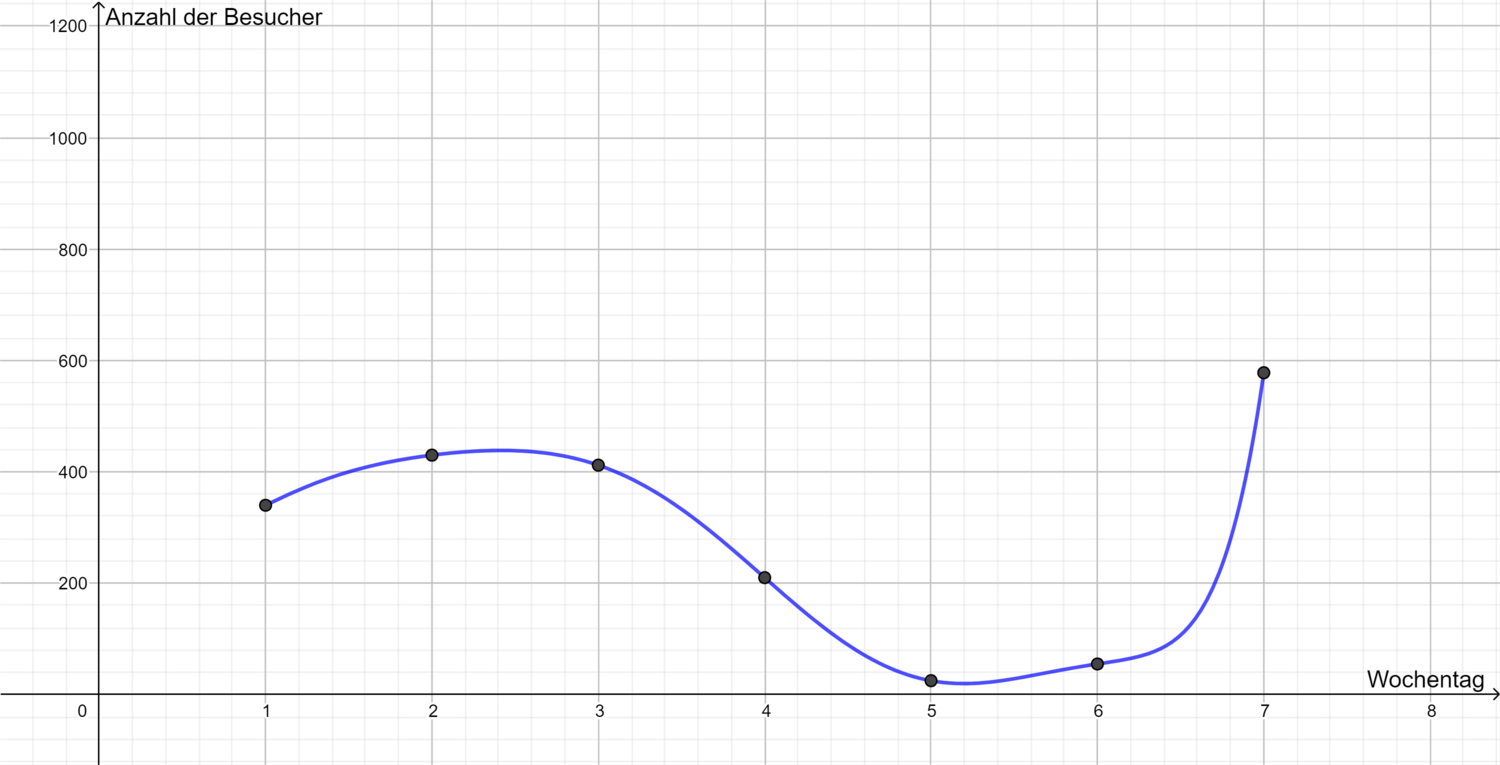
In der folgenden Tabelle sind die Besucherzahlen eines Freibades während einer Woche dargestellt. 1 = Montag, 2 = Dienstag, 3 = Mittwoch... a) Übernimm die Werte aus der Tabelle in dein Heft b) Zeichne den zugehörigen Graphen in ein Koordinatensystem. Zeichne einen Graphen der jeden Punkt berührt.
| Wochentag | Besucheranzahl |
|---|---|
| 1 | 340 |
| 2 | 430 |
| 3 | 412 |
| 4 | 680 |
| 5 | 25 |
| 6 | 55 |
| 7 | 578 |
Dein Helfer Ben der Pinguin hat die Aufgabe 1 auch erledigt. Vergleiche deine Lösung mit ihm!
![]()
Aufgabe 2
 Merke!
Merke!
Funktionen sind Zuordnungen mit einer besonderen Eigenschaft: Als Funktion bezeichnet man eine Zuordnung, die jedem Argument genau einen Wert, den Funktionswert, zuordnet. Vereinfacht gesagt:" Eine Funktion ist eine eindeutige Zuordnung."