Bruchteil, Anteil und Ganzes bei der Bruchrechnung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 111: | Zeile 111: | ||
|3=Kurzinfo}} | |3=Kurzinfo}} | ||
{{Box|1=Entdecke | {{Box|1=Entdecke einige Zusammenhänge selbstständig|2= | ||
Gehe bei der nun folgenden Übung wie folgt vor: | Gehe bei der nun folgenden Übung wie folgt vor: | ||
| Zeile 135: | Zeile 135: | ||
Mithilfe dieses Wissens kannst du bei Aufgaben, bei welchen sich eine der drei Komponenten verändert, während eine zweite gleich bleibt, deine Ergebnisse leichter überprüfen. | Mithilfe dieses Wissens kannst du bei Aufgaben, bei welchen sich eine der drei Komponenten verändert, während eine zweite gleich bleibt, deine Ergebnisse leichter überprüfen. | ||
</div> | </div> | ||
{{!)}} | {{!)}} | ||
|3=Arbeitsmethode}} | |||
Version vom 18. Oktober 2019, 11:30 Uhr
Herzlich Willkommen in dem Lernpfad "Bruchteil, Anteil und Ganzes bei der Bruchrechnung"!
Dieser Lernpfad wurde erstellt, um dein Wissen und deine Fähigkeiten im Umgang mit dem Bruchteil, Anteil und Ganzem innerhalb der Bruchrechnung zu verbessern.
Was sind nochmal Bruchteil, Anteil und das Ganze?
Immer wenn wir einen Bruch gegeben haben, dann können wir den Bruchteil , Anteil und das Ganze bestimmen. Als Ausgangspunkt dient das Ganze , von welchem nur ein bestimmter Teil betrachtet werden soll (der Bruchteil ). Der Anteil stellt immer das Verhältnis zwischen dem Bruchteil und dem Ganzen dar. Der Anteil ergibt sich, indem der Bruchteil durch das Ganze dividiert wird.
In den folgenden zwei Beispielen, kannst du dir diese drei Teile eines Bruches (Bruchteil , Anteil , Ganzes ) mithilfe von zwei Abbildungen anschauen.
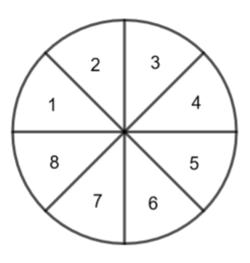
Betrachte eines Kreises.
Du siehst, dass der dargestellte Kreis in 4 gleich große Teile unterteilt ist, von denen 3 farbig markiert sind.
Der gesamte Kreis stellt bei diesem Beispiel das Ganze dar, auf welches sich der Bruchteil und der Anteil beziehen.
Die 3 farbig markierten Teile ergeben zusammen den Bruchteil .
Der Anteil gibt das Verhältnis zwischen dem Bruchteil und dem Ganzen wieder. Unterteilen wir das Ganze (den Kreis) in 4 gleich große Teile (4 Viertelkreise), dann sind 3 dieser Teile farbig markiert und einer ist nicht markiert. Also sind 3 von 4 farbig markiert (→ )Im ersten Beispiel wird das Ganze durch eine geometrische Form (Kreis) dargestellt. Du wirst aber auch mit Ganzen arbeiten müssen, welche nur aus einer Menge (Zahl) bestehen. In einem zweiten Beispiel kannst du dir anschauen, was in so einem Fall der Bruchteil , Anteil und das Ganze sind.
Betrachte nun von 12.
Wie in der Überschrift genannt, ist die 12 das Ganze (12 Sterne).
ist der Anteil und stellt wieder das Verhältnis zwischen Bruchteil und Ganzen dar. Du kannst die 12 Sterne nun in 4 Gruppen mit jeweils 3 Sternen unterteilen (dies wurde auf der linken Seite getan). Wenn du 3 dieser Gruppen nun farbig markierst, so hast du 9 Sterne markiert. Dies stellt den Bruchteil von den 12 Sternen dar.
Du kannst im nachfolgenden Lückentext überprüfen, ob du nun weißt, was Bruchteil , Anteil und Ganzes sind.
Wenn du einen Bruch in einer Sachsituation gegeben hast, dann kannst du bei dem Bruch immer Bruchteil, Anteil und Ganzes betrachten. Das Ganze stellt den Ausgangspunkt dar, auf welchen sich der Bruchteil und der Anteil beziehen. Von dem Ganzen wird meist nur ein gewisser Teil genommen. Dabei handelt es sich um den Bruchteil. Das Verhältnis zwischen Bruchteil und Ganzes spiegelt sich im Anteil wider.
Bruchteil, Anteil und Ganzes erkennen
Zusammenhänge entdecken
Gehe bei der nun folgenden Übung wie folgt vor:
- Schaue dir die angefangenen Sätze auf der rechten Seite an
- Stelle Vermutungen auf, wie sich Bruchteil, Anteil oder Ganzes in den jeweiligen Situationen verändern und schreibe deine Vermutungen auf einem Blatt Papier auf.
- Untersuche nun die Veränderungen in den Geogebra Applets. Klicke dafür einfach auf diese und verändere mithilfe der Schieberegler die jeweils zugehörige Größe.
- Vervollständige nun die Sätze und vergleiche sie mit deinen vorher aufgeschriebenen Vermutungen.
- Überprüfe nun die vervollständigten Sätze. Schaue dir noch einmal die Geogebra Applets genau an, falls die Sätze nicht richtig sind.
 |
 |
 |
Ziel dieser Aufgabe ist es, deine Entdeckungen in Geogebra in Merksätze zu formulieren.
Wird bei einer Aufgabe das Ganze größer, während der Anteil immer gleich bleibt, so wird der Bruchteil größer. Das Verhältnis zwischen Bruchteil und Ganzem bleibt gleich groß. Wird bei einer Aufgabe der Anteil kleiner, während das Ganze immer gleich groß bleibt, so wird der Bruchteil kleiner. Das Verhältnis zwischen Bruchteil und Ganzem wird kleiner. Wird bei einer Aufgabe der Bruchteil größer, während der Anteil immer gleich bleibt, so wird das Ganze größer. Das Verhältnis zwischen Bruchteil und Ganzem bleibt gleich groß. Mithilfe dieses Wissens kannst du bei Aufgaben, bei welchen sich eine der drei Komponenten verändert, während eine zweite gleich bleibt, deine Ergebnisse leichter überprüfen. |
Mit Bruchteil, Anteil und Ganzem rechnen
Der Bruchteil ist gesucht
In diesem Abschnitt ist immer der Anteil und das Ganze gegeben und es wird der Bruchteil gesucht. Wenn du nicht mehr weißt, wie du aus dem Anteil und dem Ganzen den Bruchteil bestimmen kannst, dann schaue in die nachfolgende Erklärung.
Der Bruchteil gibt die Anzahl an Teilen wider, die vom Ganzen ausgewählt werden.
Er lässt sich berechnen, indem du den Anteil mit dem Ganzen multiplizierst.
Beispiel:
Julia und Marvin besitzen zusammen 6 Mützen. davon gehören Marvin und gehören Julia. Wie viele Mützen gehören Marvin?
Rechnung: Wir multiplizieren mit 6 und erhalten .
Berechne nun selbst in deinem Heft den Bruchteil in den dargestellten Aufgaben. Kürze dabei soweit wie möglich.
Nachdem du alle Bruchteile berechnet hast, überprüfe selbst deine Lösung, indem du zu jeder Aufgabe den jeweiligen Bruchteil ziehst.
Du multiplizierst einen Bruch mit einer natürlichen Zahl, indem du den Zähler mit der natürlichen Zahl multiplizierst und den Nenner beibehältst.
Beispiel:
Der Bruch soll mit der natürlichen Zahle multipliziert werden. Wir multiplizieren dann den Zähler () mit der natürlichen Zahl und behalten den Nenner () bei.
→
Alternativ kannst du schon vorher kürzen.
Ganze: 32 Anteil:
oder
Ganze: 60 Anteil:
oder
Ganze: 200 Anteil:
oder
Ganze: 36 Anteil:
oder
Ganze: 35 Anteil:
oder
Das Ganze ist gesucht
In diesem Abschnitt ist immer der Bruchteil und der Anteil gegeben und es wird das Ganze gesucht.
Wenn du nicht mehr weißt, wie du aus dem Bruchteil und dem Anteil das Ganze bestimmen kannst, dann schaue in die nachfolgende Erklärung.
Das Ganze stellt die Ausgangsgröße dar.
Du erhältst das Ganze aus dem Bruchteil und dem Anteil indem du den Bruchteil durch den Anteil dividierst.
Beispiel:
Julia gehören 2 Mützen für den Winter. Das sind aller Mützen, die sie und ihr Bruder Marvin gemeinsam besitzen. Wie viele Mützen haben die beiden zusammen?
Rechnung: Wir teilen 2 durch und erhalten .
Berechne nun selbst in deinem Heft das Ganze in den dargestellten Aufgaben.
Nachdem du alle Ganze berechnet hast, überprüfe selbst deine Lösung, indem du zu jeder Aufgabe das jeweilige Ganze ziehst.
Du kannst eine natürliche Zahl durch einen Bruch dividieren, indem du die natürliche Zahl mit dem Kehrbruch des gegebenen Bruchs dividierst. Der Kehrbruch zu einem gegebenen Bruch erhältst du, indem du Zähler und Nenner des Bruchs vertauschst.
Beispiel:
Die natürliche Zahl 2 soll durch dividiert werden. Der Kehrbruch von ist . Wir multiplizieren nun 2 mit dem Kehrbruch ()
→
Auch hierbei kann schon früher gekürzt werdenBruchteil: 8 Anteil:
Bruchteil: 18 Anteil:
oder
Bruchteil: 15 Anteil:
oder
Bruchteil: 22 Anteil:
oder
Bruchteil: 9 Anteil:
oder
Der Anteil ist gesucht
In diesem Teil ist immer der Bruchteil und das Ganze gegeben und es wird der Anteil gesucht.
Wenn du nicht mehr weißt, wie du aus dem Bruchteil und dem Ganzen den Anteil bestimmen kannst, dann schaue in die nachfolgende Erklärung.
Der Anteil stellt das Verhältnis zwischen dem Bruchteil und dem Ganzen dar.
Er lässt sich berechnen, indem du den Bruchteil durch das Ganze dividierst.
Beispiel:
Julia und Marvin besitzen zusammen 6 Mützen. Vier davon gehören Marvin und zwei gehören Julia. Wie groß ist der Anteil von Julias Mützen an allen Mützen der beiden?
Rechnung: Wir teilen 2 durch 6 und erhalten .
Berechne nun selbst in deinem Heft die Anteile der dargestellten Aufgaben. Kürze dabei soweit wie möglich.
Nachdem du alle Anteile berechnet hast, überprüfe selbst deine Lösung, indem du zu jeder Aufgabe den jeweiligen Anteil ziehst.
Ganze: 75 Bruchteil: 45
Ganze: 360 Bruchteil: 280
Ganze: 26 Bruchteil: 8
Ganze: 28 Bruchteil: 10
Ganze: 24 Bruchteil: 4
Teste zum Schluss dein Wissen
Du kannst bei gegebenen Situationen erkennen, was Bruchteil, Anteil und Ganzes sind und nach welcher dieser drei Größen gefragt ist? Zusätzlich kannst du den Bruchteil, Anteil und das Ganze berechnen, wenn diese gesucht sind?
Dann teste in dem folgenden Quiz dein können und schaffe es Bruch-Millionär zu werden!
Berechne dafür die Ergebnisse auf einem Blatt Papier und kreuze die richtige Antwort an.
Viel Erfolg!
Bruchteil: Anteil:
Ganze ist gesucht:
oder
Ganze: Bruchteil:
Anteil ist gesucht:
Ganze: Anteil: Es gibt Rabatt auf den Schal, also beträgt der noch zu zahlende Anteil
Bruchteil ist gesucht:
oder
Ganze: Anteil von Amy: Anteil von Emil:
Um den Bruchteil von Alicia zu berechnen, werden erst die Bruchteile von Amy und Emil berechnet und die Summe der beiden von der Gesamtanzahl der Stimmen subtrahiert.
Bruchteil von Amy:
Bruchteil von Emil:
Zusammen haben Amy und Emil bei der Klassensprecherwahl 17 Stimmen erhalten. Alicia hat alle anderen Stimmen bekommen, daher ist der Bruchteil von Alicia:
Bruchteil: Anteil:
Ganze ist gesucht:
Ganze: Bruchteil:
Anteil ist gesucht: