Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Die Ableitung als lokale lineare Approximation

Grundvorstellungen zum Ableitungsbegriff
Die Ableitung als lokale Änderungsrate

Für diese Grundvorstellung werden Sie verschiedene Funktionen unter die Lupe nehmen und feststellen wie sich diese in kleinen Umgebungen um einen Punkt verhalten.

Bild einfügen

Aufgabe 1

a) Zoomen Sie vermehrt an den Punkt A. Was stellen Sie fest? Beschreiben sie Ihre Beobachtung?

zum Applet

b) Was erwarten Sie, wenn Sie an den Punkt B zoomen? Überprüfen Sie Ihre Vermutung mit dem Applet. Beschreiben Sie Ihre Vermutung und was Sie festgestellt haben.

zum Applet

c) An welchen Stellen des Funktionsgraphen würde es beim Hineinzoomen ebenfalls so aussehen wie um den Punkt B?

Wenn wir beim Hineinzoomen in einen Funktionsgraphen bemerken, dass dieser aussieht wie eine Gerade, nennen wir diese Funktion ,,lokal linear" an diesem Punkt.

Aufgabe 2

In dieser Aufgabe werden Sie Funktionen untersuchen in denen die lokale Linearität nicht auf Anhieb ersichtlich ist. Geben Sie im Applet die kritischen Punkte ein die Sie untersuchen möchten und überprüfen Sie die lokale Linearität durch Hineinzoomen.
a) $f(x)= \sqrt{x^2}$ zum Applet
b) $g(x)=100x^2$ zum Applet

c) $h(x)=|x^2-4|$ zum Applet

Wenn man beim Hineinzoomen in einem Punkt feststellt, dass die Funktion an dieser Stelle lokal linear ist, nennen wir die Funktion an dieser Stelle differenzierbar.

Aufgabe 3

Nun werden Sie mit Hilfe des Funktionenmikroskop die Steigung einer Funktion in einem bestimmten Punkt bestimmen.
a) Zoomen Sie in diesem Applet vermehrt in den Punkt A hinein und schieben Sie B durch Verkleinerung von h näher an A heran. Berechnen Sie mit Hilfe des Differenzenquotienten die Steigung, die der Graph ,,im" Punkt A hat so genau wie möglich.
Tipp: Mit den Pfeiltasten lässt sich der Schieberegler feiner ändern.

Hier die Lösung der Rechnung

Differentialquotient

Der Differenzenquotient $\frac{f(x_0+h)-f(x_0)}{h}$ kommt der Steigung im Punkt $P (x_0,f(x_0))$ beliebig nahe, je näher $h$ der Null kommt.

Dieser Grenzwert des Differenzenquotienten ist der Differentialquotient $f'(x_0) = \lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}$.
Der Differentialquotient $f'(x_0)$ wird auch als Ableitung der Funktion $f$ an der Stelle $x_0$ bezeichnet.

b) Welches Problem kann bei der Verschiebung von B gegen A auftreten? Was muss für die Bestimmung der Steigung gewährleistet sein?

c) Betrachten Sie in diesem Applet die Sekante durch die Punkte A und B und verschieben erneut den Punkt B gegen A. Beschreiben Sie die Gerade die entsteht.

Hier die Lösung

Differentialquotient

Der Differenzenquotient $\frac{f(x_0+h)-f(x_0)}{h}$ kommt der Steigung im Punkt $P (x_0,f(x_0))$ beliebig nahe, je näher $h$ der Null kommt.

Dieser Grenzwert des Differenzenquotienten ist der Differentialquotient $f'(x_0) = \lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}$.
Der Differentialquotient $f'(x_0)$ wird auch als Ableitung der Funktion $f$ an der Stelle $x_0$ bezeichnet.

Die Tangente als lokale lineare Approximation

Wie du in den Aufgaben zuvor schon gesehen hast, lässt sich der Graph der Funktion in einer kleinen Umgebung sehr gut durch die Tangente nähern.

Aufgabe 4

Arbeitsmethode

Aufgabe 5

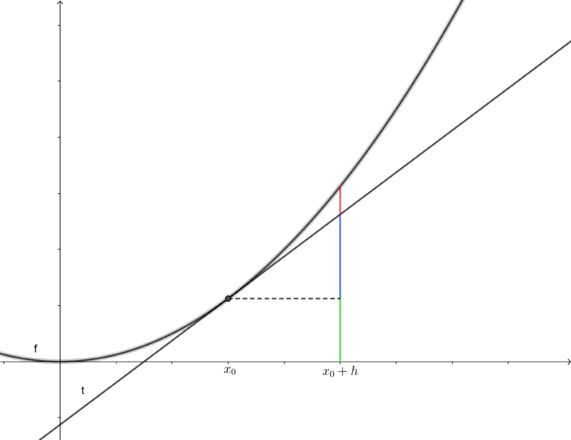
Bestimmen Sie durch Addition der farbigen Strecken die allgemeine Gleichung zur Berechnung der Werte für $f(x_0+h)$. Nutzen Sie als Hilfe das folgende Applet.

Aufgabe 6

Lassen Sie nun den Approximationsfehler für kleine h außer Acht und betrachten die Näherungsfunktion $f(x_0+h) =f(x_0)+f'(x_0)*h$ Stellen Sie die Gleichung nach $f'(x)$ um. Was fällt Ihnen auf?