Die Ableitung als Steigung der Tangente: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 2: | Zeile 2: | ||
==Die Tangente== | ==Die Tangente== | ||
Sie hatten bereits in der Sekundarstufe 1 mit Tangenten zu tun und haben diese im Zusammenhang mit kreisen kennengelernt.{{Box|Aufgabe 1|a) | Sie hatten bereits in der Sekundarstufe 1 mit Tangenten zu tun und haben diese im Zusammenhang mit kreisen kennengelernt.{{Box|Aufgabe 1|a) In [[Aufgabe 1a)|diesem Applet]] sehen Sie zwei verschiedene Tangenten. Nennen Sie Unterschiede und Gemeinsamkeiten der beiden Tangenten <br/> | ||
{{Lösung versteckt|1=Text zum Verstecken|2=Lösung anzeigen|3=Lösung verbergen}} | {{Lösung versteckt|1=Text zum Verstecken|2=Lösung anzeigen|3=Lösung verbergen}} | ||
Version vom 30. Juni 2019, 15:23 Uhr
Die Tangente
Sie hatten bereits in der Sekundarstufe 1 mit Tangenten zu tun und haben diese im Zusammenhang mit kreisen kennengelernt.
a) In diesem Applet sehen Sie zwei verschiedene Tangenten. Nennen Sie Unterschiede und Gemeinsamkeiten der beiden Tangenten
b) Zoomen Sie in diesem Applet in den Berührpunkt der Tangente und beschreiben Sie sie sehen.
c) Zoomen Sie in diesem Applet in den Berührpunkt der Tangente und beschreiben Sie sie sehen.
Die Steigung einer Sekante
a) Wie ist eine Sekante,wie Sie sie im obigen Bild sehen können, definiert?
b) Berechnen Sie die Steigung der Sekante in diesem Applet.
c) Stellen Sie die allgemeine Gleichung zur Berechnung der Steigung von Sekanten auf.
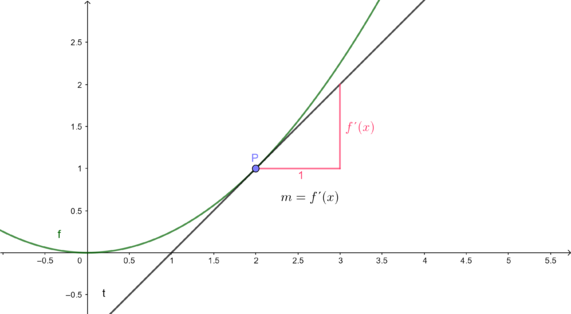
Die Steigung der Tangente
a) Wie ist eine Sekante,wie Sie sie im obigen Bild sehen können, definiert?
b) Berechnen Sie die Steigung der Sekante in diesem Applet.
c) Stellen Sie die allgemeine Gleichung zur Berechnung der Steigung von Sekanten auf.