Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Die Ableitung als lokale Änderungsrate: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Benutzer:PascalHänle/Grundvorstellungen zum Ableitungsbegriff/Die Ableitung als lokale Änderungsrate
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 43: | Zeile 43: | ||
}}Überprüfe deine Ergebnisse mit Hilfe des geometrischen Zusammenhangs der mittleren Änderungsrate und der Sekantensteigung. | }}Überprüfe deine Ergebnisse mit Hilfe des geometrischen Zusammenhangs der mittleren Änderungsrate und der Sekantensteigung. | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
<ggb_applet id="ceu9yjy3" width="100%" height="450" border=" | <ggb_applet id="ceu9yjy3" width="100%" height="450" border="200">Weg - Zeit - Kurve Porsche </ggb_applet> | ||
}} | }} | ||
Version vom 12. April 2019, 15:02 Uhr
Porsche
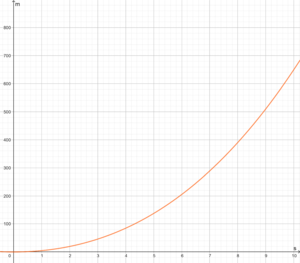
Die folgende Tabelle zeigt den Beschleunigungsvorgang des Rennautos Porsche 918 Spyder. Die Weg - Zeit - Kurve lässt sich in diesem Intervall annähernd durch die Funktion ... beschreiben.
Zeit (Sekunden) Strecke (Meter) 0 0 1 4,7 2 19,6 3 45,9 4 84,8 5 137,5 6 205,2 7 289,1 8 390,4 9 510,3
mittlere Änderungsrate
Überlegen sie zunächst welcher physikalischen Größe der mittleren Änderungsrate in diesem Beispiel zuzuordnen ist und wie man diese berechnet.
Aufgabe 1
Bestimmen Sie mit welcher Durchschnittsgeschwindigkeit der Porsche in den folgenden Zeitintervallen gefahren ist.
a) zwischen Sekunde 1 und 2
b) zwischen Sekunde 2 und 3
c) zwischen Sekunde 3 und 4
Überprüfe deine Ergebnisse mit Hilfe des geometrischen Zusammenhangs der mittleren Änderungsrate und der Sekantensteigung.
