Zentrische Streckung/Abbildung durch zentrische Streckung/5.Station

1. Station: Ähnlichkeitsabbildung - Exkurs: Weitere Beispiele einer zentrischen Streckung - 2. Station: Streckungsfaktor - Fortsetzung der 2. Station: Streckungsfaktor - 3. Station: Berechnung der Streckenlängen und des Streckungsfaktors - 4. Station: Zusammenfassung - 5. Station: Übung - 6. Station: Wissenswertes

5. Station: Übung

1. Aufgabe

Ordne zuerst die Buchstaben so, dass sinvolle Wörter entstehen, und löse dann das Kreuzworträtsel!

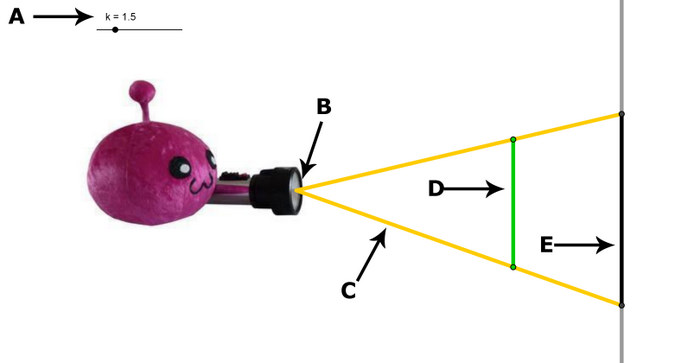
Das Bild zeigt eine zentrische Streckung.

Streckungsfaktor Was kann man mit Hilfe des Schiebereglers (A) einstellen? Streckungszentrum Was stellt die Taschenlampe (B) dar? Halbgerade Was ist der Lichtstrahl (C)? Urbild Als was kann man den Strohhalm (D) noch bezeichnen? Bild Als was kann man den Schatten (E) noch bezeichnen?

2. Aufgabe

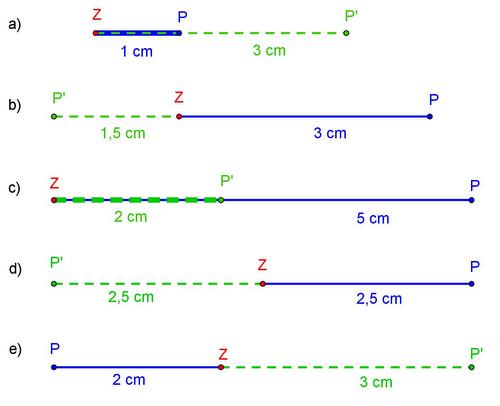
Berechne den Streckungsfaktor k in deinem Heft! Ordne danach die richtige Lösung zu:

a) k = 3 b) k = -0,5 c) k = 0,4 d) k = -1 e) k = -1,5

3. Aufgabe

Verschiebe in diesem Applet das Streckungszentrum Z und die Urpunkt P und Q mit der Maus, sodass sie mit den angegebenen Koordinaten für jede Teilaufgabe übereinstimmen!
Führe dann die zentrische Streckung mit gegebenem Zentrum und Streckungsfaktor durch, indem du die Punkt P' und Q' an die richtige Stelle verschiebst! Beantworte die Fragen zu den Teilaufgaben, die neben dem Applet stehen, um herauszufinden ob du die Punkte richtig verschoben hast!
Im Moment siehst du ein Beispiel bei dem Z(-1|1), P(1|2) und Q(1|0) ist und die zentrische Streckung mit k = 2 durchgeführt wurde.

a) Z(0|0), k= 3, P(-1|1), Q(2|1)
b) Z(1|1), k= -2.5, P(3|1), Q(3|3)
c) Z(3|1), k= 0.5, P(3|3), Q(1|1)

---

Die Datei [INVALID] wurde nicht gefunden.

a) Wie lang ist P'Q'? P'Q' = 9 (Trage hier die Länge ein) LE b)Welche Koordinaten hat P' und welche Q'? P'(-4 (Trage hier die x- Koordinate von P' ein)|1 (Trage hier die y- Koordinate von P' ein)) Q'(-4 (Trage hier die x- Koordinate von P' ein)|-4 (Trage hier die y- Koordinate von P' ein)) c)Welche Koordinaten hat P' und wie lang ist ZQ' P'(3 (Trage hier die x- Koordinate von P' ein)|2 (Trage hier die y- Koordinate von P' ein)) ZQ' = 1 (Trage hier die Länge ein) LE

$\Rightarrow$ Weiter zur 6. Station: Wissenswertes

$\Leftarrow$ Zurück zur 4. Station: Zusammenfassung