Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Einführung in die Integralrechnung: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 7: | Zeile 7: | ||
<br>'''Materialien:'''{{pdf|Infini_AB1.pdf|Das bestimmte Integral}}; {{pdf|Infini AB02.pdf|Aufgaben mit Lösung}}; {{pdf|Infini_AB7.pdf|Integralfunktion}}|Lernpfad}} | <br>'''Materialien:'''{{pdf|Infini_AB1.pdf|Das bestimmte Integral}}; {{pdf|Infini AB02.pdf|Aufgaben mit Lösung}}; {{pdf|Infini_AB7.pdf|Integralfunktion}}|Lernpfad}} | ||
__NOTOC__ | |||
==Das Flächenproblem== | ==Das Flächenproblem== | ||
Version vom 18. November 2018, 16:57 Uhr
Lernpfad
In diesem Lernpfad können die Schüler die grundlegenden Zusammenhänge der Integralrechnung anhand vieler interaktiver Übungen entdecken.
Materialien: Das bestimmte Integral;
Das bestimmte Integral;  Aufgaben mit Lösung;
Aufgaben mit Lösung;  Integralfunktion
Integralfunktion
Einige Übungen sind dem gleichnamigen Lernpfad Einführung in die Integralrechnung der österreichischen Arbeitsgruppe Medienvielfalt im Mathematikunterricht entnommen, die aus einer Kooperation von mathe-online und GeoGebra entstanden ist.
Voraussetzungen:
Zeitbedarf: etwa 3 Schulstunden
Materialien:
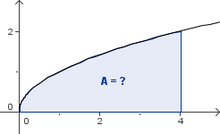
Das Flächenproblem
Ziel der folgenden Überlegungen ist es, ein Verfahren zu entwickeln, mit dem Flächeninhalte von krummlinig begrenzten Flächen berechnet werden können.
|
Unter- und Obersumme
- Begriffsklärung Unter- und Obersumme
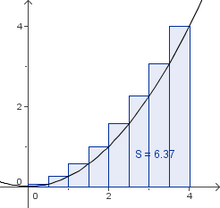
- Aufgabe: Gegeben ist die Funktion f(x) = 0.25 x².
- Zerlege das Intervall [0;4] in 8 gleichlange Teilintervalle und skizziere den Graphen und die Rechtecke in dein Heft.
- Berechne die zugehörige Ober- und Untersumme.
- Gib auch das arithmetische Mittel von Ober- und Untersumme als Näherungswert für die Fläche unter dem Funktionsgraphen an.
- Lösung:
0 0,5 1 1,5 2 2,5 3 3,5 4
-----------------------------------------------------------f(x)
- Berechnung von Unter- und Obersummen mit GeoGebra
Das bestimmte Integral
- Informiere dich im
 Arbeitsblatt "Das bestimmte Integral" über die Definition des Begriffs "bestimmtes Integral".
Arbeitsblatt "Das bestimmte Integral" über die Definition des Begriffs "bestimmtes Integral". - Auf dem
 Arbeitsblatt sind für einige einfache Funktionen die bestimmten Integrale über dem Intervall [a;b] angegeben. Finde anschauliche Erklärungen für die Herleitung und berechne die bestimmten Integrale für die angegeben Werte!
Arbeitsblatt sind für einige einfache Funktionen die bestimmten Integrale über dem Intervall [a;b] angegeben. Finde anschauliche Erklärungen für die Herleitung und berechne die bestimmten Integrale für die angegeben Werte!  Lösung
Lösung - Berechne: ; ;
- Überprüfe die Lösung mit folgendem
 Applet, in dem du mit Hilfe der Schieberegler die Integrationsgrenzen anpasst!
Applet, in dem du mit Hilfe der Schieberegler die Integrationsgrenzen anpasst!
Flächenberechnung
- Aufgaben zur Flächenberechnung mit Geogebra
- Kläre die Bedeutung des Begriffs "negativer Flächeninhalt"!
- Erkläre den Unterschied zwischen dem Wert des bestimmten Integrals und dem Flächeninhalt zwischen Graph und x-Achse!
Integralfunktion
- Bearbeite die Punkte 1 bis 6 des dynamischen Arbeitsblatts zur Integralfunktion. Halte die Ergebnisse in deinem Heft fest.
- Überlege: Welche Funktionen der Kurvenschar sind keine Integralfunktionen?
- Bearbeite nun als Zusammmenfassung das
 Arbeitsblatt "Die Integralfunktion".
Arbeitsblatt "Die Integralfunktion".
Zusätzliche Übungsaufgaben
Für Interessierte
- Hauptsatz der Differential- und Integralrechnung mit ausführlichem Beweis
- Informiere dich im Internet über die Geschichte der Integralrechnung.
- Bei welchen Fragestellungen kommt die Integralrechung zum Einsatz? Finde möglichst vielfältige Beispiele.
<metakeywords>ZUM2Edutags,ZUM-Wiki,Mathematik-digital,Einführung in die Integralrechnung,Mathematik,Einführung,Integralrechnung,12. Klasse,Oberstufe,Lernpfad</metakeywords>