Integralrechnung/Vorüberlegungen

Vorlage:Kasten blau

Frage

Aber wie kann man diesen Flächeninhalt denn nun genau bestimmen bzw. berechnen?

Dies ist die zentrale Frage des vorliegenden Lernpfades!

Um der Lösung näher zu kommen, fangen wir mit einfachen und sehr speziellen Graphen von Funktionen an und arbeiten uns ausgehend davon immer weiter hin zu schwierigeren und allgemeineren Graphen von Funktionen, damit wir am Ende eine Lösung für alle Eventualitäten in Händen halten!
Vorlage:Aufgaben-M
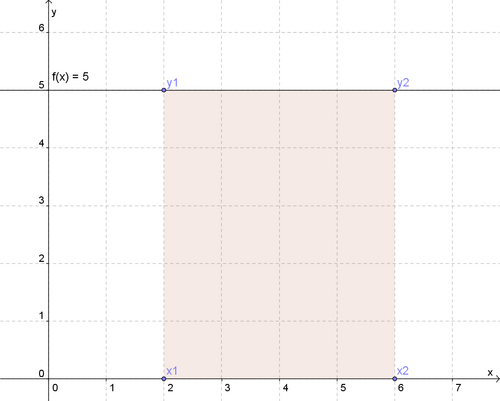
a) Konstante Funktion:   $f(x)=5$   in den Grenzen $x_1=2$ und $x_2=6$

Vorlage:Lösung

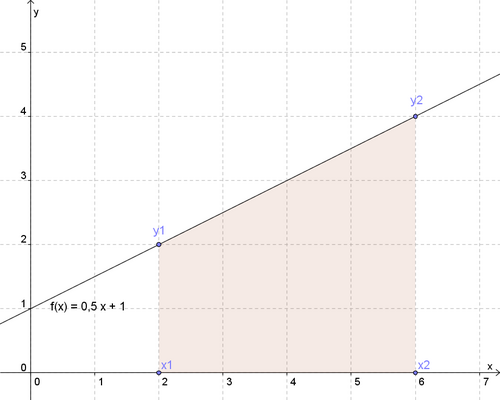
b) Lineare, nicht-konstante Funktion:   $f(x)= 0,5 x + 1$   in den Grenzen $x_1=2$ und $x_2=6$

Vorlage:Lösung

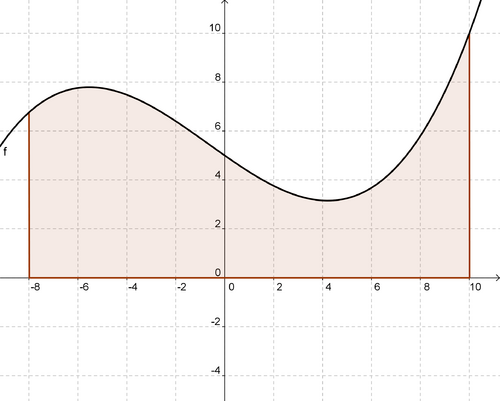
c) Ausgehend von den Aufgabenteilen a) und b) sollst Du hier nur eine Möglichkeit beschreiben, wie man die schraffierte Fläche zumindest näherungsweise bestimmen könnte. Dazu soll eine Funktion dritten Grades als Beispiel für eine Funktion im Allgemeinen dienen: $f(x) = \frac{1}{100} \cdot x^3 + \frac{1}{50} \cdot x^2 - \frac{7}{10} \cdot x + 5$   in den Grenzen -8 und 10.

<<Zurück<<     Home     >>Weiter>>