Ganzrationale Funktionen: Unterschied zwischen den Versionen
Main>MarinaMueller KKeine Bearbeitungszusammenfassung |
Main>MarinaMueller KKeine Bearbeitungszusammenfassung |
||
| Zeile 46: | Zeile 46: | ||
<br> | <br> | ||
2) Ein Eintrag nach jeder Stunde während der gesamten Unterrichtseinheit - mögliche Fragen, an denen du dich dabei orientieren kannst, sind: | 2) Ein Eintrag nach jeder Stunde während der gesamten Unterrichtseinheit - mögliche Fragen, an denen du dich dabei orientieren kannst, sind: | ||
* Was habe ich gelernt? Was habe ich gut verstanden, welche Fragen sind noch offen? Welche Schwierigkeiten sind bei der Lösung aufgetreten? | ::* Was habe ich gelernt? Was habe ich gut verstanden, welche Fragen sind noch offen? Welche Schwierigkeiten sind bei der Lösung aufgetreten? | ||
* An welchen Stellen habe ich etwas für mich Neues gelernt? Hatte ich Aha-Erlebnisse? | ::* An welchen Stellen habe ich etwas für mich Neues gelernt? Hatte ich Aha-Erlebnisse? | ||
* Bin ich mit meiner Arbeit zufrieden? Habe ich mein Arbeitsziel in dieser Stunde erreicht? Wenn nicht, woran lag es? | ::* Bin ich mit meiner Arbeit zufrieden? Habe ich mein Arbeitsziel in dieser Stunde erreicht? Wenn nicht, woran lag es? | ||
* Wie habe ich mich in dieser Stunde im Unterricht oder in der Gruppenarbeit beteiligt? Welche Note würde ich mir geben? | ::* Wie habe ich mich in dieser Stunde im Unterricht oder in der Gruppenarbeit beteiligt? Welche Note würde ich mir geben? | ||
3) Abschlusskommentar zu jeder Phase der Unterrichtseinheit: | 3) Abschlusskommentar zu jeder Phase der Unterrichtseinheit: | ||
<br> | <br> | ||
| Zeile 182: | Zeile 182: | ||
<br> | <br> | ||
<br> | <br> | ||
=== Symmetrie === | === Symmetrie === | ||
{{Arbeiten|NUMMER=5|ARBEIT=Bei welcher der Funktionen kannst du eine Symmetrie erkennen (Punktsymmetrie zum Ursprung oder Achsensymmetrie zur y-Achse)? Gruppiere die Funktionen bzw. die Funktionsgleichungen entsprechend in drei Gruppen (Punktsymmetrie, Achsensymmetrie, keine Symmetrie). Formuliere einen Merksatz, woran man eine mögliche Symmetrie an der Funktionsgleichung erkennen kann.}} | {{Arbeiten|NUMMER=5|ARBEIT=Bei welcher der Funktionen kannst du eine Symmetrie erkennen (Punktsymmetrie zum Ursprung oder Achsensymmetrie zur y-Achse)? Gruppiere die Funktionen bzw. die Funktionsgleichungen entsprechend in drei Gruppen (Punktsymmetrie, Achsensymmetrie, keine Symmetrie). Formuliere einen Merksatz, woran man eine mögliche Symmetrie an der Funktionsgleichung erkennen kann.}} | ||
| Zeile 194: | Zeile 196: | ||
}} | }} | ||
<br> | <br> | ||
=== Verhalten im Unendlichen / Verlauf des Graphen === | === Verhalten im Unendlichen / Verlauf des Graphen === | ||
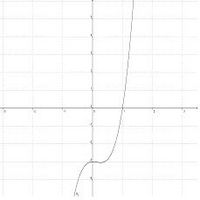
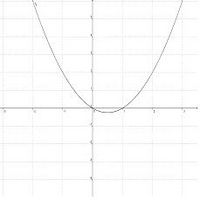
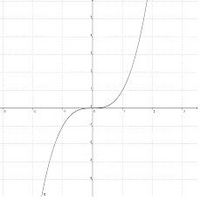
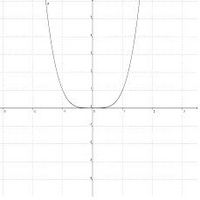
{{Arbeiten|NUMMER=6|ARBEIT=Wie verhalten sich die verschiedenen Graphen <br> | {{Arbeiten|NUMMER=6|ARBEIT=Wie verhalten sich die verschiedenen Graphen <br> | ||
* für sehr große x-Werte? | ::* für sehr große x-Werte? | ||
* für sehr kleine x-Werte? <br> | ::* für sehr kleine x-Werte? <br> | ||
Gruppiere die Funktionen begründet entsprechend ihres Verhaltens und formuliere in deinem Lerntagebuch einen Merksatz, woran man das Verhalten der Funktion für sehr große bzw. sehr kleine x-Werte ablesen kann.}} | Gruppiere die Funktionen begründet entsprechend ihres Verhaltens und formuliere in deinem Lerntagebuch einen Merksatz, woran man das Verhalten der Funktion für sehr große bzw. sehr kleine x-Werte ablesen kann.}} | ||
| Zeile 207: | Zeile 211: | ||
}} | }} | ||
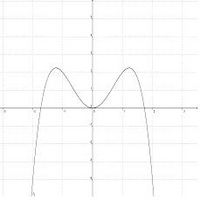
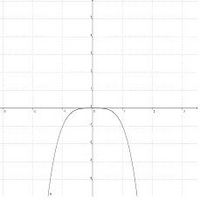
{{Arbeiten|NUMMER=7|ARBEIT=Betrachte die folgenden Graphen:<br> | {{Arbeiten|NUMMER=7|ARBEIT=Betrachte die folgenden Graphen:<br> | ||
| Zeile 254: | Zeile 256: | ||
<br> | <br> | ||
<br> | <br> | ||
== '''Transformationen''' == | == '''Transformationen''' == | ||
Die ganzrationalen Funktionen, die du in diesem Lernpfad kennen gelernt hast, weisen bestimmte Transformationen auf, d. h. die Funktionsgleichung gibt an, inwiefern der Graph gestreckt oder gestaucht, in Richtung der x- oder y-Achse verschoben oder an der x-Achse gespiegelt ist. | Die ganzrationalen Funktionen, die du in diesem Lernpfad kennen gelernt hast, weisen bestimmte Transformationen auf, d. h. die Funktionsgleichung gibt an, inwiefern der Graph gestreckt oder gestaucht, in Richtung der x- oder y-Achse verschoben oder an der x-Achse gespiegelt ist. | ||
<br> | <br> | ||
| Zeile 262: | Zeile 267: | ||
{{Arbeiten|NUMMER=8|ARBEIT=Skizziere und beschreibe das Aussehen von | {{Arbeiten|NUMMER=8|ARBEIT=Skizziere und beschreibe das Aussehen von | ||
* Geraden und | ::* Geraden und | ||
* Parabeln | ::* Parabeln | ||
in deinem Lerntagebuch. Erläutere jeweils den Einfluss der Koeffizienten auf die Graphen, sofern dieser eindeutig zu erkennen ist. Falls du Hilfe brauchst, nutze das versteckte Applet.}} | in deinem Lerntagebuch. Erläutere jeweils den Einfluss der Koeffizienten auf die Graphen, sofern dieser eindeutig zu erkennen ist. Falls du Hilfe brauchst, nutze das versteckte Applet.}} | ||
{{versteckt|<ggb height="" width="" showMenuBar="false" showResetIcon="true" filename=" .ggb" />}} | {{versteckt|<ggb height="" width="" showMenuBar="false" showResetIcon="true" filename=" .ggb" />}} | ||
| Zeile 274: | Zeile 279: | ||
<br> | <br> | ||
Stelle anschließend allgemein zusammen, durch welche Veränderung in der Funktionsgleichung f(x) = a<sub>1</sub>x + a<sub>0</sub> du die jeweilige Transformation, d. h. | Stelle anschließend allgemein zusammen, durch welche Veränderung in der Funktionsgleichung f(x) = a<sub>1</sub>x + a<sub>0</sub> du die jeweilige Transformation, d. h. | ||
* eine Streckung in Richtung der y-Achse um den Faktor a , | ::* eine Streckung in Richtung der y-Achse um den Faktor a , | ||
* eine Spiegelung des Funktionsgraphen an der x-Achse, | ::* eine Spiegelung des Funktionsgraphen an der x-Achse, | ||
* eine Verschiebung in Richtung der y-Achse um e | ::* eine Verschiebung in Richtung der y-Achse um e | ||
* eine Verschiebung in Richtung der x-Achse um d | ::* eine Verschiebung in Richtung der x-Achse um d | ||
darstellen kannst. Du kannst deine Vermutungen mit verschiedenen Beispielen in [http://www.geogebra.org GeoGebra] überprüfen. | darstellen kannst. Du kannst deine Vermutungen mit verschiedenen Beispielen in [http://www.geogebra.org GeoGebra] überprüfen. | ||
Kannst du in einer Gleichung zusammenfassen: Streckung in Richtung der y-Achse um a, Verschiebung in Richtung der y-Achse um e, Verschiebung in Richtung der x-Achse um d? Formuliere einen Satz, der Auskunft darüber gibt, wie du eine lineare Funktion an der x-Achse spiegeln kannst.}} | Kannst du in einer Gleichung zusammenfassen: Streckung in Richtung der y-Achse um a, Verschiebung in Richtung der y-Achse um e, Verschiebung in Richtung der x-Achse um d? Formuliere einen Satz, der Auskunft darüber gibt, wie du eine lineare Funktion an der x-Achse spiegeln kannst.}} | ||
| Zeile 286: | Zeile 291: | ||
{{Arbeiten|NUMMER=10|ARBEIT=Eine Streckung bzw. Stauchung in Richtung der x-Achse kann erreicht werden durch Bilden von f(bx) mit einem gegebenen Wert für b, d. h. überall dort, wo in der Funktionsgleichung ein x steht, wird bx eingesetzt und aufgelöst. Untersuche, für welche Werte von b sich die drei Möglichkeiten ergeben: Streckung, Stauchung, keine Veränderung. Nimm die Funktion f(x) und experimentiere mit [http://www.geogebra.org GeoGebra]. Beschreibe deine Versuche und Ergebnisse kurz in deinem Lerntagebuch.}}<br> | {{Arbeiten|NUMMER=10|ARBEIT=Eine Streckung bzw. Stauchung in Richtung der x-Achse kann erreicht werden durch Bilden von f(bx) mit einem gegebenen Wert für b, d. h. überall dort, wo in der Funktionsgleichung ein x steht, wird bx eingesetzt und aufgelöst. Untersuche, für welche Werte von b sich die drei Möglichkeiten ergeben: Streckung, Stauchung, keine Veränderung. Nimm die Funktion f(x) und experimentiere mit [http://www.geogebra.org GeoGebra]. Beschreibe deine Versuche und Ergebnisse kurz in deinem Lerntagebuch.}}<br> | ||
{{Lösung versteckt|Folgende Fälle lassen sich unterscheiden: | {{Lösung versteckt|Folgende Fälle lassen sich unterscheiden: | ||
* -1 < b < 1: Streckung in Richtung der x-Achse; dazu kommt für negative Werte die Spiegelung an der y-Achse <br> | ::* -1 < b < 1: Streckung in Richtung der x-Achse; dazu kommt für negative Werte die Spiegelung an der y-Achse <br> | ||
* b = 1: keine Veränderung, im negativen Fall nur Spiegelung an der y-Achse | ::* b = 1: keine Veränderung, im negativen Fall nur Spiegelung an der y-Achse | ||
* b < -1 bzw. b > 1: Stauchung in Richtung der x-Achse; dazu kommt für negative Fälle die Spiegelung an der y-Achse}} <br> | ::* b < -1 bzw. b > 1: Stauchung in Richtung der x-Achse; dazu kommt für negative Fälle die Spiegelung an der y-Achse}} <br> | ||
Automatisch hast du jetzt also auch schon die '''Spiegelung an der y-Achse''' als weitere Transformationsart mit bearbeitet. | Automatisch hast du jetzt also auch schon die '''Spiegelung an der y-Achse''' als weitere Transformationsart mit bearbeitet. | ||
| Zeile 328: | Zeile 333: | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
{{Merke|1=Eine Streckung bzw. Stauchung einer ganzrationalen Funktion wird erreicht durch die Multiplikation der '''gesamten''' Funktion mit dem Streckfaktor a. Für a lassen sich drei verschiedene Fälle unterscheiden: <br> | {{Merke|1=Eine Streckung bzw. Stauchung einer ganzrationalen Funktion wird erreicht durch die Multiplikation der '''gesamten''' Funktion mit dem Streckfaktor a. Für a lassen sich drei verschiedene Fälle unterscheiden: <br> | ||
* -1 < a < 1: Es handelt sich um eine Stauchung; im Falle eines negativen Streckfaktors kommt eine Spiegelung an der x-Achse hinzu. | ::* -1 < a < 1: Es handelt sich um eine Stauchung; im Falle eines negativen Streckfaktors kommt eine Spiegelung an der x-Achse hinzu. | ||
* a = 1: Die Funktionsgleichung ändert sich nicht, es handelt sich weder um eine Stauchung noch um eine Streckung. | ::* a = 1: Die Funktionsgleichung ändert sich nicht, es handelt sich weder um eine Stauchung noch um eine Streckung. | ||
* a > 1 bzw. a < -1: Es handelt sich um eine Streckung. Für negatives a ist es zusätzlich eine Spiegelung an der x-Achse. <br> | ::* a > 1 bzw. a < -1: Es handelt sich um eine Streckung. Für negatives a ist es zusätzlich eine Spiegelung an der x-Achse. <br> | ||
Durch eine Streckung oder Stauchung ändern sich alle Werte der Funktion mit Ausnahme der Nullstellen - Nullstellen bleiben von Streckungen (bzw. Stauchungen) in Richtung der y-Achse grundsätzlich unberührt.}} | Durch eine Streckung oder Stauchung ändern sich alle Werte der Funktion mit Ausnahme der Nullstellen - Nullstellen bleiben von Streckungen (bzw. Stauchungen) in Richtung der y-Achse grundsätzlich unberührt.}} | ||
}} <br> | }} <br> | ||
| Zeile 353: | Zeile 358: | ||
Beschreibe anhand der folgenden Bilder kurz in deinem Lerntagebuch, wie der Graph zu g aus dem Graphen zu f hervorgeht. Gegeben sind die Funktionsgleichungen <br> | Beschreibe anhand der folgenden Bilder kurz in deinem Lerntagebuch, wie der Graph zu g aus dem Graphen zu f hervorgeht. Gegeben sind die Funktionsgleichungen <br> | ||
* <math>f(x) = 3x^3 - 4x^2 + 1</math> | ::* <math>f(x) = 3x^3 - 4x^2 + 1</math> | ||
* <math>g(x) = 3(x - 3)^3 - 4(x - 3)^2 + 1 - 2 = 3x^3 - 31x^2 + 60x - 64</math> | ::* <math>g(x) = 3(x - 3)^3 - 4(x - 3)^2 + 1 - 2 = 3x^3 - 31x^2 + 60x - 64</math> | ||
Wo finden sich die Verschiebungen in der Funktionsgleichung wieder? Kannst du eine Gleichung der Form g(x) = ... aufstellen, in der du allgemein f(x) nutzt (anstatt 3x^3 - 4x^2 + 1) und die ausdrückt, dass f um 3 Einheiten in Richtung der x-Achse und um 2 Einheiten in Richtung der y-Achse verschoben ist?} <br> | Wo finden sich die Verschiebungen in der Funktionsgleichung wieder? Kannst du eine Gleichung der Form g(x) = ... aufstellen, in der du allgemein f(x) nutzt (anstatt 3x^3 - 4x^2 + 1) und die ausdrückt, dass f um 3 Einheiten in Richtung der x-Achse und um 2 Einheiten in Richtung der y-Achse verschoben ist?} <br> | ||
| Zeile 391: | Zeile 396: | ||
* <math>f(\frac{1}{2}x) = 2(\frac{1}{2}x)^3 - 6(\frac{1}{2}x)^2 + 3(1/2x)</math> | * <math>f(\frac{1}{2}x) = 2(\frac{1}{2}x)^3 - 6(\frac{1}{2}x)^2 + 3(1/2x)</math> | ||
* Die Fallbetrachtungen für b können übertragen werden. | * Die Fallbetrachtungen für b können übertragen werden. | ||
* | * Ersetzbar?????}} | ||
<br> | <br> | ||
<br> | <br> | ||
| Zeile 397: | Zeile 402: | ||
=== Zusammenfassung === | === Zusammenfassung === | ||
{{Arbeiten|NUMMER=18|Fasse zusammen, was du über Transformationen von ganzrationalen Funktionen gelernt hast. Erstelle eine Liste mit den Transformationsarten und der jeweiligen Einbindung in die Funktionsgleichung.}} | {{Arbeiten|NUMMER=18|Fasse zusammen, was du über Transformationen von ganzrationalen Funktionen gelernt hast. Erstelle eine Liste mit den Transformationsarten und der jeweiligen Einbindung in die Funktionsgleichung.}} | ||
<br> | <br> | ||
<br> | <br> | ||
== '''Zusatzaufgabe''' == | == '''Zusatzaufgabe''' == | ||
{{Kasten_blau|Falls du vor der vereinbarten Zeit mit der Bearbeitung des Lernpfades fertig sein solltest, entwirf ein kleines Funktionenbild oder -muster mithilfe von ganzrationalen Funktionen. Nutze dazu [http://www.geogebra.org GeoGebra].}} | {{Kasten_blau|Falls du vor der vereinbarten Zeit mit der Bearbeitung des Lernpfades fertig sein solltest, entwirf ein kleines Funktionenbild oder -muster mithilfe von ganzrationalen Funktionen. Nutze dazu [http://www.geogebra.org GeoGebra].}} | ||
Version vom 21. November 2010, 22:59 Uhr
|
Herzlich willkommen zum Lernpfad zu ganzrationalen Funktionen!
In unserer aktuellen Unterrichtseinheit geht es um Transformationen von verschiedenen Funktionen, d. h. also, ihr sollt herausarbeiten, mithilfe welcher Operationen bzw. Veränderungen in der Funktionsgleichung unterschiedliche Funktionsarten im Koordinatensystem verschoben, gestreckt bzw. gestaucht und gespiegelt werden können. In diesem Lernpfad sollst du dich nun speziell mit den ganzrationalen Funktionen auseinandersetzen. Kompetenzen
|
Infos vor Beginn
1) Lerntagebuch:
Während der gesamten Unterrichtseinheit sollst du ein Lerntagebuch führen: Das Tagebuch dient einerseits als "normales" Heft und andererseits als Reflexionsinstrument. Das heißt, du sollst nicht nur die gegebenen Arbeitsaufträge im Lerntagebuch bearbeiten, sondern dir darüber hinaus auch (schriftlich) Gedanken über deine Lernfortschritte und die Eignung des Arbeitsmaterials machen. Das Tagebuch wird nicht bewertet, es dient ausschließlich dazu, dir selbst klar zu machen, wie groß dein Lernfortschritt ist und wo vielleicht noch Probleme liegen.
Folgende Bestandteile sollte das Tagebuch haben:
1) Standortbestimmung: Was weiß ich bereits über Funktionstransformationen im Allgemeinen? Weiß ich bereits etwas über die zu bearbeitenden Funktionsarten?
2) Ein Eintrag nach jeder Stunde während der gesamten Unterrichtseinheit - mögliche Fragen, an denen du dich dabei orientieren kannst, sind:
- Was habe ich gelernt? Was habe ich gut verstanden, welche Fragen sind noch offen? Welche Schwierigkeiten sind bei der Lösung aufgetreten?
- An welchen Stellen habe ich etwas für mich Neues gelernt? Hatte ich Aha-Erlebnisse?
- Bin ich mit meiner Arbeit zufrieden? Habe ich mein Arbeitsziel in dieser Stunde erreicht? Wenn nicht, woran lag es?
- Wie habe ich mich in dieser Stunde im Unterricht oder in der Gruppenarbeit beteiligt? Welche Note würde ich mir geben?
3) Abschlusskommentar zu jeder Phase der Unterrichtseinheit:
4) Allgemeine Beurteilung der Einheit: Waren Aufbau und Material sinnvoll (speziell die Lernpfade)?
5) Abschlussprodukt: Funktionenbild mit Erläuterung
2) Allgemeine Hinweise:
- Bearbeite den Lernpfad mit einem Partner oder einer Partnerin - so könnt ihr gemeinsam über die Aufgaben sprechen und schneller zu sinnvollen Ergebnissen gelangen.
- Nutze die versteckten Hinweise erst, wenn du allein bzw. ihr zu zweit bei der Aufgabe nicht mehr weiter kommt - versucht es zuerst ohne Hilfe!
- Für die versteckten Lösungen gilt: Schau sie dir erst an, wenn du die Aufgabe gelöst hast - sie dienen nur der Kontrolle!
- Übernimm alle wichtigen Definitionen, Merksätze, Erläuterungen in dein Lerntagebuch - im Regelfall wirst du allerdings an der betreffenden Stelle explizit dazu aufgefordert.
- ...
Definition der ganzrationalen Funktionen
Eine kleine Aufgabe zum Einstieg:
Vorlage:Arbeiten
Die Funktion, die du gerade aufgestellt hast, ist eine sogenannte ganzrationale Funktion - sie setzt sich zusammen aus den einzelnen Summanden , und , den Potenzfunktionen. Der höchste Exponent gibt den Grad der Funktion an, d. h. es handelt sich hier um eine ganzrationale Funktion dritten Grades. Die Vorfaktoren der einzelnen Summanden werden entsprechend den zugehörigen Exponenten von x mit - bezeichnet (, , ) - sie heißen Koeffizienten.
Nun in allgemeiner Form:
Ein Term der Form mit ; , , , ..., , und heißt Polynom. Die Zahlen , , , , ..., , nennt man Koeffizienten des Polynoms. Als Grad des Polynoms wird der höchste Exponent n von x bezeichnet, dessen zugehöriger Koeffizient nicht Null ist.
Eine Funktion f, deren Funktionswert f(x) als Polynom geschrieben werden kann, heißt ganzrationale Funktion.
Nicht erschrecken, die Definition sieht viel komplizierter aus als das Ganze in Wirklichkeit ist. Hier nochmal langsam zum Üben:
Mit den folgenden Übungen kannst du überprüfen, ob du alles verstanden hast:
Vorlage:Arbeiten
1) Grad: 7, Koeffizienten:
2) Grad: 0, Koeffizienten:
3) Grad: 1, Koeffizienten:
4) Grad: 6, Koeffizienten: ,
Entscheide: Handelt es sich um eine ganzrationale Funktion? Begründe in deinem Lerntagebuch.
Wichtige Eigenschaften ganzrationaler Funktionen
Im Folgenden sollst du die gerade geordneten Funktionen noch einmal genauer untersuchen hinsichtlich möglicher Symmetrien sowie ihrem Verhalten für sehr große und sehr kleine x (Verhalten im Unendlichen):
Symmetrie
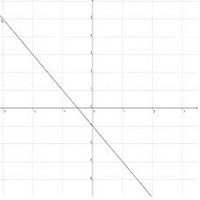
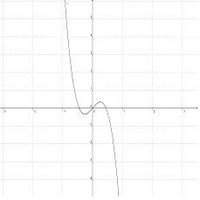
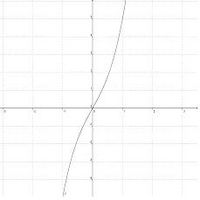
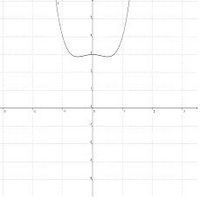
Der Graph einer ganzrationalen Funktion f verläuft genau dann
- achsensymmetrisch zur y-Achse, wenn f(x) nur Potenzen mit geraden Exponenten enthält.
- punktsymmetrisch zum Ursprung, wenn f(x) nur Potenzen mit ungeraden Exponenten enthält.
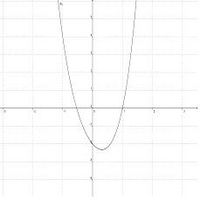
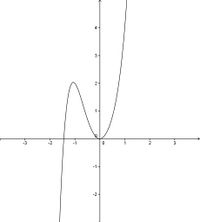
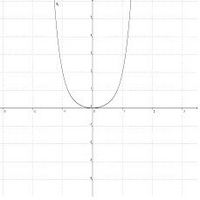
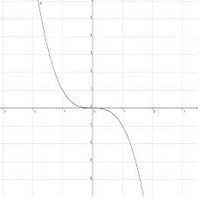
Verhalten im Unendlichen / Verlauf des Graphen
Mithilfe der folgenden Übung kannst du Verlauf und Symmetrie von ganzrationalen Funktionen untersuchen und so überprüfen, ob du alles verstanden hast.
Transformationen
Die ganzrationalen Funktionen, die du in diesem Lernpfad kennen gelernt hast, weisen bestimmte Transformationen auf, d. h. die Funktionsgleichung gibt an, inwiefern der Graph gestreckt oder gestaucht, in Richtung der x- oder y-Achse verschoben oder an der x-Achse gespiegelt ist.
Mit zwei Arten von ganzrationalen Funktionen hast du dich in den vergangenen Wochen im Unterricht bereits näher beschäftigt, und zwar mit den linearen und den quadratischen Funktionen. Dabei handelt es sich um nichts anderes als um ganzrationale Funktionen ersten und zweiten Grades. Eine lineare Funktion wird entsprechend der Definition als Polynom folgendermaßen geschrieben: - der zugehörige Graph heißt - wie du weißt - Gerade. Die dementsprechende Schreibweise der quadratischen Funktionen sieht folgendermaßen aus: (Normalform) - der zugehörige Graph heißt Parabel.
Vorlage:Arbeiten
Vorlage:Versteckt
Im Folgenden sollst du dich genauer mit Verschiebungen, Streckungen / Stauchungen und Spiegelungen von ganzrationalen Funktionen (speziell dritten und vierten Grades) beschäftigen. Los geht es mit den einfachsten ganzrationalen Funktionen - den Geraden. Mit verschiedenen Aspekten im Zusammenhang mit linearen Funktionen hast du dich im Unterricht zwar schon beschäftigt, aber noch nicht mit Transformationen von Geraden im Koordinatensystem. Das sollst du nun nachholen:
Eine Transformationsart, die bislang noch nicht betrachtet wurde, ist die Streckung / Stauchung in Richtung der x-Achse.
Vorlage:Arbeiten
Automatisch hast du jetzt also auch schon die Spiegelung an der y-Achse als weitere Transformationsart mit bearbeitet.
Die Möglichkeit, die Normalform in die Scheitelpunktform zu überführen, ist allerdings nur bei quadratischen Funktionen so einfach möglich. Ganzrationale Funktionen mit n > 2 werden im Regelfall in Polynomschreibweise angegeben und lassen sich nicht in eine Art "Scheitelpunktform" überführen, an der alle Transformationsarten ablesbar sind.
Auch für diese Fälle gibt es eine solche Funktionsgleichung, aber die Auseinandersetzung damit ist nicht die Aufgabe eurer Gruppe, sondern die der Gruppe "Potenzfunktionen". Ihr sollt euch mit der etwas schwierigeren Polynomschreibweise auseinandersetzen.
Du hast ja bereits herausgefunden, wie die verschiedenen Transformationen sich bei linearen Funktionen (also den einfachsten der ganzrationalen Funktionen) in die Funktionsgleichung einbauen lassen; im Folgenden sollst du versuchen, dein Wissen bezüglich der einzelnen Transformationsarten auf ganzrationale Funktionen zweiten, dritten und vierten Grades zu übertragen.
Beginnen wir mit der Streckung bzw. Stauchung in Richtung der y-Achse:
{{Arbeiten|NUMMER=13|ARBEIT=Du siehst auf dem folgenden Bild zwei Funktionsgraphen: f(x) ist die Ausgangsfunktion mit der angezeigten Funktionsgleichung - g(x) ist demgegenüber in Richtung der y-Achse gestreckt. Bestimme die Funktionsgleichung zu g(x).
<ggb height="" width="" showMenuBar="false" showResetIcon="true" filename=" .ggb" />
- Bestimme zuerst den Faktor a, mit dem du f(x) strecken oder stauchen musst, um g(x) zu erhalten.
- Durch welche mathematische Operation kannst du nun zur Funktionsgleichung von g(x) kommen?
- Welche Punkte des Graphen verändern sich durch eine Streckung in Richtung der y-Achse, welche nicht?
- Stauche f(x) um den Faktor a= Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac {1}{2}<math>. Wie lautet die Funktionsgleichung zur neuen Funktion h(x)? Überprüfe mit dem GeoGebra-Link unten. <br> * Überprüfe mithilfe des Links, ob deine Erkenntnisse sich auch auf Funktionen dritten und vierten Grades übertragen lassen. Welche Fälle für a lassen sich unterscheiden? Wähle für jeden Fall zwei entsprechende Beispiele und überprüfe - notiere in deinem Lerntagebuch. Was ändert sich im Fall a < 0? * Formuliere einen Merksatz, der erklärt, wie du eine beliebige ganzrationale Funktion mit einem Faktor strecken oder stauchen kannst (Wie muss der Faktor jeweils aussehen?). Welche Punkte des Graphen werden durch eine Streckung / Stauchung nicht verändert? <br> Falls du nicht weiter weißt, nutze den versteckten Hinweis. Falls du zeichnerisch ausprobieren möchtest, kannst du das hier tun: [http://www.geogebra.org GeoGebra].}} <br> {{versteckt|Zur Bestimmung des Streckfaktors wähle dir einen Wert, also z. B. x = 1. Lies die zugehörigen Funktionswerte für beide Funktionen an den Graphen ab - in welcher Beziehung stehen die beiden Funktionswerte zueinander? Überprüfe mithilfe weiterer Werte und überlege dir, wie du diesen Streckfaktor mit der Funktionsgleichung von f in Verbindung setzen kannst.}} <br> {{Lösung versteckt| {{Merke|1=Eine Streckung bzw. Stauchung einer ganzrationalen Funktion wird erreicht durch die Multiplikation der '''gesamten''' Funktion mit dem Streckfaktor a. Für a lassen sich drei verschiedene Fälle unterscheiden: <br> ::* -1 < a < 1: Es handelt sich um eine Stauchung; im Falle eines negativen Streckfaktors kommt eine Spiegelung an der x-Achse hinzu. ::* a = 1: Die Funktionsgleichung ändert sich nicht, es handelt sich weder um eine Stauchung noch um eine Streckung. ::* a > 1 bzw. a < -1: Es handelt sich um eine Streckung. Für negatives a ist es zusätzlich eine Spiegelung an der x-Achse. <br> Durch eine Streckung oder Stauchung ändern sich alle Werte der Funktion mit Ausnahme der Nullstellen - Nullstellen bleiben von Streckungen (bzw. Stauchungen) in Richtung der y-Achse grundsätzlich unberührt.}} }} <br> Mit Bearbeitung dieser Aufgabe hast du bereits implizit die '''Spiegelung an der x-Achse'' mit untersucht und damit bereits eine weitere Transformationsart "abgehakt". Bevor du dich der nächsten Transformationsart zuwendest, hier noch einige Übungen zu Streckungen und Stauchungen: <br> Weiter geht es mit den '''Verschiebungen in Richtung der beiden Achsen''': <br> Der Abwechselung halber betrachten wir nun eine Funktion 3. Grades. {{Arbeiten|NUMMER=14|ARBEIT= <br> <ggb height="" width="" showMenuBar="" showResetIcon="" filename=" .ggb" /> <br> Beschreibe anhand der folgenden Bilder kurz in deinem Lerntagebuch, wie der Graph zu g aus dem Graphen zu f hervorgeht. Gegeben sind die Funktionsgleichungen <br> ::* <math>f(x) = 3x^3 - 4x^2 + 1}
Wo finden sich die Verschiebungen in der Funktionsgleichung wieder? Kannst du eine Gleichung der Form g(x) = ... aufstellen, in der du allgemein f(x) nutzt (anstatt 3x^3 - 4x^2 + 1) und die ausdrückt, dass f um 3 Einheiten in Richtung der x-Achse und um 2 Einheiten in Richtung der y-Achse verschoben ist?}
Nun ein konkretes Beispiel:
Vorlage:Arbeiten
Kleine Übung zum Verschieben von ganzrationalen Funktionen:
Zum Abschluss noch die Streckung / Stauchung in Richtung der x-Achse:
Vorlage:Arbeiten
- Die Fallbetrachtungen für b können übertragen werden.
- Ersetzbar?????
Zusammenfassung