Anwendungsbezogene Extremwertaufgaben

Extremwertaufgaben in der Anwendung

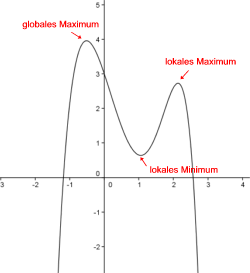
Als Extremwert einer Funktion wird derjenige Wert bezeichnet, der innerhalb eines gewissen Bereichs größer (Maximum) bzw. kleiner (Minimum) als alle anderen Werte in diesem Bereich ist. Hierbei wird noch zwischen einem lokalen und einem globalen Extremwert unterschieden. Global ist der Extremwert dann, wenn er der größte bzw. kleinste Wert im gesamten Definitionsberich ist, im anderen Fall ist es ein lokaler Extremwert.

Formal ist er folgendermaßen definiert:

Es sei $U \subseteq\mathbb R$ eine Teilmenge der Reellen Zahlen (z.B. ein Intervall) und $f\colon U\to\mathbb R$ eine Funktion.

f hat an der Stelle $x_0\in U$

• ein lokales Minimum, wenn es ein Intervall $I = (a,b)$ gibt, das $x_0$ enthält, so dass $f(x_0)\leq f(x)$ für alle $x\in I\cap U$ gilt;

• ein globales Minimum, wenn $f(x_0)\leq f(x)$ für alle $x\in U$ gilt;

• ein lokales Maximum, wenn es ein Intervall $I = (a,b)$ gibt, das $x_0$ enthält, so dass $f(x_0)\geq f(x)$ für alle $x\in I\cap U$ gilt;

• ein globales Maximum, wenn $f(x_0)\geq f(x)$ für alle $x\in U$ gilt.

Wozu überhaupt Extremwerte?

Extremwerte geben maximale bzw. minimale Größen bei vorgegebenen Randbedingungen an und sind Lösungen bei sogenannten Optimierungsproblemen, d.h. sie geben den idealen Zusammenhang der Funktionsgrößen wieder. So kann durch die Bestimmung des Extremwertes herausgefunden werden, welche Verpackungsform das geringste Material verbraucht, unter welchen Parametern eine Strecke in kürzester Zeit zurückgelegt werden kann usw.

Allgemeines Lösungsverfahren

Ein Extremwert einer Funktion tritt immer dort auf, wo die 1. Ableitung dieser Funktion eine Nullstelle hat und die zweite 2. Ableitung keine Nullstelle besitzt (Alternativ können hier statt der 2. Ableitung auch die Vorzeichen der ersten Ableitung betrachtet werden. Bei Vorzeichenwechsel liegt dann ein Extremwert vor).

Ist allerdings wie bei praktischen Problemen keine explizite Funktion vorgegeben, sondern nur das Problem formuliert, muss zunächst eine passende Funktion, die Zielfunktion, aufgestellt werden. Hierbei hilft es, sich an folgendes Schema zu halten:

1. Stelle das Problem in einer Skizze dar

Eine Skizze hilft, sich die Problemstellung deutlich zu machen. Kennzeichne in der Skizze die bekannten und unbekannten Größen. Überlege dir, welche Größen in der Skizze du noch nicht weißt und ob du diese durch die anderen Größen ermitteln kannst.

2. Stelle die Zielfunkion auf

Versuche nun, deine Skizze in eine Funktion zu übertragen. Hierbei musst du die Größe, die du maximieren oder minimieren willst, durch die anderen vorhandenen Größen ausdrücken.

3. Nebenbedingung in Zielfunktion einsetzen

Unter Nebenbedingung versteht man einen für die Aufgabe notwendigen Zusammenhang, der nicht direkt aus der Aufgabenstellung hervorgeht. Ist in der Zielfunktion also noch eine Größe, die du nicht kennst, versuche sie durch die anderen gegebenen Größen z.B. mit Hilfe eines geometrischen Zusammenhangs auszudrücken. Am Schluss darf deine Zielfunktion nur noch von einer Größe abhängen.

4. Extremwert der Zielfunktion bestimmen

Nun musst du nur noch den Extremwert der Zielfunktion herausfinden. Dies geschieht durch Nullstetzen der ersten Ableitung und durch die Betrachtung des Randes der Definitionsmenge. Betrachtest du die Nullstelle der ersten Ableitung, so musst du diesen Wert noch durch einsetzen in die 2. Ableitung überprüfen. Ist die 2. Ableitung an dieser Stelle positiv, so handelt es sich um eine Minimum, ist sie negativ, um ein Maximum. Falls die 2. Ableitung ebenfalls eine Nullstelle hat, ist es kein Extremum.

Der schräge Wurf

Als erstes Beispiel wollen wir untersuchen, in welchem Winkel du einen Ball nach vorne oben werfen musst, um eine möglichst große Wurfweite zu erzielen und welche maximale Höhe der Ball dabei jeweils erreicht. Hierzu sind natürlich einige Vorüberlegungen zu treffen. Von was hängt die Wurfweite sonst noch ab? Erinnerst du dich an die entsprechenden physikalischen Formeln? Wenn du dich nicht erinnern kannst oder um deine Formeln zu überprüfen, klicke auf Lösung anzeigen! Aber: Vorher nachdenken!

Versuche nun nach dem oben dargestellten Schema vorzugehen, dir also in einer Skizze die Situation zu verdeutlichen und die entsprechenden Größen einzuzeichnen! Wo befindet sich der Winkel $\alpha$?

Skizze:

Als feste Größe ist die Abwurfgeschwindigkeit $\vec v_{0}$ anzusehen. Dies ist die Geschwindigkeit, die du durch deine Wurfbewegung dem Ball in einer bestimmten Richtung mitgibst. Der entscheidende Parameter ist der Winkel $\alpha$. Kannst du die noch unbekannten Größen mit Hilfe von $\vec v_{0}$ und $\alpha$ ausdrücken?

Nun kannst du die beiden Ortsgleichungen aufschreiben und zu einer Funktionsgleichung umformen. Die Zielfunktion ist dabei die Funktion der Größe, die du maximieren willst. In unserem Fall möchten wir zunächst das Maximum der Wurfweite in Abhängigkeit des Abwurfwinkels bestimmen. Unsere Zielfunktion ist also die Ortsfunktion in x-Richtung. Versuche diese Funktion mit Hilfe der bisherigen Gleichungen aufzustellen.

Vorlage:Lösung versteckt mit Rand

Nun musst du dir klar werden, welche Größen du darstellen willst! In unserem Fall: Wurfweite x in Abhängigkeit des Wurfwinkels $\alpha$. Steht dies schon da? Oder steht in der Funktion eine Variable, die stört bzw. nicht gegeben ist? Dann musst du diese Variable durch deine eigentlich interessanten Größen ausdrücken, oder anders gesagt, eine Nebenbedinung formulieren. Tipp: Nicht erschrecken vor zunächst etwas unhandlichen Termen.

Falls du nicht weiterkommst, findest du hier die Nebenbedingung mit entsprechender Auflösung: Vorlage:Lösung versteckt mit Rand

Wenn du die Nebenbedingung formuliert hast und umgeformt hast, kannst du die störende Variable durch für die Aufgabe wesentliche Größen ausdrücken. Dies musst du nun in die Zielfunktion einsetzen.

Du hast nun die Zielfunktion aufgestellt und die störende Variable durch deine Nebenbedingung elimiert. Nun hast du eine Funktion, die dir die Wurfweite in Abhängigkeit des Winkels darstellt. Wir wollen den Winkel herausfinden, bei dem die Wurfweite maximal wird. Wir suchen also das Maximum von $x(\alpha)$.

Dieses Maximum können wir bestimmen, indem wir die Funktion einmal ableiten und die Nullstellen dieser Ableitung suchen. Da die Funktion nur von $\alpha$ abhängt, musst du jetzt natürlich nach $\alpha$ ableiten. Versuche, die Nullstelle zu bestimmen.

Extremwertaufgabe mit Nebenbedingung: Acker neben Straße

Aufgabe

Ein Acker liegt an einer geradlinigen Straße. Ein Fußgänger befindet sich auf dem Acker im Punkt A und möchte möglichst schnell zu einem Punkt B auf der Straße gelangen. Der Fußpunkt C des Lotes von A auf die Straße hat von A die Entfernung 400m und die Entfernung B nach C betrage

(a.) 1000m

(b.) 100m.

Auf der Straße kann sich der Fußgänger doppelt so schnell fortbewegen wie auf dem Acker. Welchen Weg soll er einschlagen?

                  Versuche zuerst die Aufgabe ohne Hilfestellung zu lösen!

                   Ansonsten löse die Aufgabe in folgenden Schritten:

1. Stelle die Aufgabensituation in einer Skizze dar:

Beschrifte, was gegeben und gesucht ist. Gebe den Bekannten und Unbekannten passende Namen.

Skizze "Acker neben Straße"

2. Zielfunktion für Teilaufgabe a) :

Erkenne die Zielfunktion und formuliere sie als mathematische Funktion in Abhängigkeit von den Ausgangsgrößen und Unbekannten.

Zielfunktion

3. Nebenbedingung in Zielfunktion für Teilaufgabe a):

Erkenne die Nebenbedingung, die unabhängige Größen der Zielfunktion zueinander in Beziehung setzt, formuliere sie als mathematischen Ausdruck und setze sie in die Zielfunktion so ein, dass eine äquivalente Zielfunktion für den zu optimierenden Wert in Abhängigkeit von nur einer Variablen entsteht.

Zielfunktion mit Nebenbedingung

4. Bestimmung des Extremwertes der Zielfunktion für Teilaufgabe a) und b):

Bestimmung des Extremwertes durch Nullsetzen der ersten Ableitung und Überprüfung des Vorzeichens der zweiten Ableitung.

Extremwertbestimmung

Vorlage:Mitgewirkt