Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Einführung in quadratische Funktionen/Übungen 3: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Navigation verstecken| | |||
{{Quadratische Funktionen}} | |||
|Lernschritte einblenden | |||
|Lernschritte ausblenden | |||
}} | |||
__NOTOC__ | |||
==Welche Funktionsgleichung stimmt?== | ==Welche Funktionsgleichung stimmt?== | ||
| Zeile 91: | Zeile 98: | ||
* [http://www.studienseminare-ge-gym.nrw.de/K/riemer/mathematik/publikationen/videoanalyse/index-videoanalyse.htm Videoanalyse: Geschwindigkeit und Bremswege] von [http://www.riemer-koeln.de/joomla/ Wolfgang Riemer] | * [http://www.studienseminare-ge-gym.nrw.de/K/riemer/mathematik/publikationen/videoanalyse/index-videoanalyse.htm Videoanalyse: Geschwindigkeit und Bremswege] von [http://www.riemer-koeln.de/joomla/ Wolfgang Riemer] | ||
---- | |||
{{ | {{Quadratische Funktionen}} | ||
Version vom 18. Oktober 2018, 22:31 Uhr
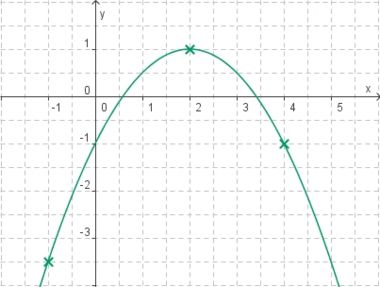
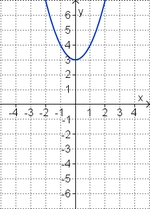
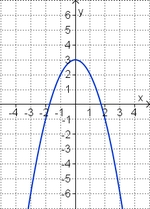
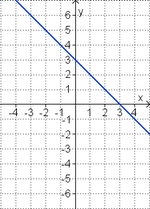
Welche Funktionsgleichung stimmt?
Gleichung und Graph zuordnen
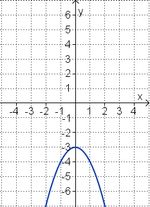
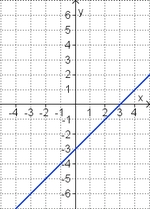
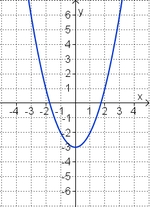
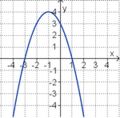
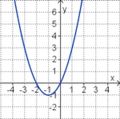
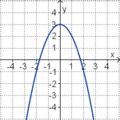
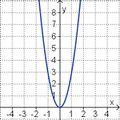
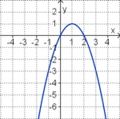
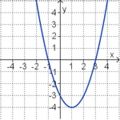
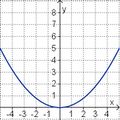
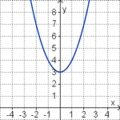
Ordne den Funktionsgraphen die richtigen Gleichung zu.
Kreuze jeweils alle richtigen Aussagen an
<b>f
<br> <b>Welche Terme gehören zu einer Funktion, deren Graph symmetrisch zur y-Achse ist?</b>
<br> <b>Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der y-Achse symmetrisch zueinander sind?</b>
<br> <b>Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der x-Achse symmetrisch zueinander sind?</b>
Memo-Quiz
Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen).
*Zusatz: Weitere interaktive Übungen
Weiterführende Links