Main>Tanjaweis |
Main>Tanjaweis |
| Zeile 35: |
Zeile 35: |
| Wenn es dir schwer fällt, dir das Ganze richtig vorzustellen, nimm dir vorne am Pult zwei der Bierdeckelstapel und stelle die einzelnen Situationen damit nach.}} | | Wenn es dir schwer fällt, dir das Ganze richtig vorzustellen, nimm dir vorne am Pult zwei der Bierdeckelstapel und stelle die einzelnen Situationen damit nach.}} |
| <br> | | <br> |
| <ggb_applet width="1584" height="717" version="4.0" ggbBase64="UEsDBBQACAgIADlzXUEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAA5c11BAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1d23LbOJq+7nkKlLeqq2c6ZogzkHZ6Komdo3PqnGZz46IkWmYsUWqScuzU3O/9PsM8wW7VXM3V9pvsk+wPgpQlkZREWZJpb1JJJJIgQXz/Ad8P/ID2/nre76EzP4qDQXh/BzvuDvLD9qAThN37O6PkeFft/PXXP+11/UHXb0UeOh5EfS+5v8NMyaADtxyzdluJzq5QAu8y7rd2NXXpLsMu83y/hSXr7CB0Hgf3wsErr+/HQ6/tv2uf+H3vcND2krTikyQZ3rt79+vXr05elTOIune73ZZzHsMD4DXD+P5O9uUePG7qpq80LU5cF9/928tD+/jdIIwTL2z7O8g0YRT8+qcf9r4GYWfwFX0NOskJvL1woR0nftA9gUYpAQd3TakhIDL020lw5sdw78Rh2uikP9xJi3mhuf6D/YZ64/bsoE5wFnT86P6O6xCOleQ7aBAFfphkJXBW0938GXtngf/VPsx8S+thOygZDHotzzwH/f3viLjERXfMB7YfBD6EsJdce86l9oPYD2Y/uC3D7O3MFmW2DLNlGN1BZ0EctHr+/Z1jrxcDcEF4HIHQxsdxctHz0/fJTly2Gd+BNsXBNyhMDaoWaTjvunfMP4D6DnMzhCcaiSdqTaJRzUrzKjFXbPk6yZVaSvNKmUuLdRJe0U4xp1Lb8OUaOoEtVJX+Tf8VaqTzmjlboz2+WoWCbaWJe3dzW9nLzAPFJ6Zspj6J34+NwVCNuDZ6jxEH4xAS1JwjrOFDEgTmgDBHjMMhVkiYT4mohAsMUaSQKYcpSq2DK/iPyfRhAnF4mDkrwSgRhooY4hTh1KgYAlNCqWGCkRIKJThHHG4y1WNiHkEFYgKOqEIM3tHYpMRQkMKNcAzVE0QxouZmLBERSJjnYWZsXSjz6vBIgoSLBDYPBLMGk7bmDOUVoqY1IoMrCIejZAqidr+Tf00Gw7EsoDQ4pEtnZx3UlC/8Ya/ntfwe9A/vjCQROvN6xiLSio4HYYJyIQp7rht5w5OgHb/zkwTuitEX78w79BL//DGUjvO607LtQRi/iQbJo0Fv1A9jhNqDnjt+50EPT3wn47eGAzpxgU1e4BMXxMR3WVrvAK6gUexD/YMozot7nc4zU+LSNQCSr8PexcPI906Hg2C6GXt3065mzx+1e0En8MKPoKymFoMLGvc8qb/Kex6hdP4mg6jz7iIGFUbnn/1ocH9nlxOHSIEZEZIqwST4nAt7iRHqaEkI4VRRTomAXiZue8b6uHKEFFIzAXdRjRlcuqi+llbun42F5J37l+3tRsFYXcz3Z/HDQa8zvpwi8MgbJqMopQ3wfpFp1oOw2/NTLUkdLvTJ7dPW4PydVQ9qn/X+YghHrn2BVjdFHoF3IBxeuJt9tuxnWsa82biUm5Zx0xJurm9BZ/FTQIHtq2UtxXkriZtXE8SpT3N3MsvJ/ZVRf9PDj8IgOcwPkqB9mjUV2xtejfot/1KJTIH9wPIRqMWZrQZvtBrTNqAkcfI3Q0j4Tvr93ye+vz/xEy89JpRrJSWH/4lWymr0jC7vnfpR6Pcy0wGNGQ1GsfUEE1bV8dtBHw7tBZI12CjFB2iTPdvxu5Gflfd6KfGzYkmvupNGUTidPupxNOg/C8/eg8bNvMDe3fwt9+J2FAyNYqMWdDen/qXuQts96K06k/cZWwc026ZXAkATg/ZH45H8EJgy1Bm0T9AZXPt8AWoEJC88wj+To+PgPPCjxEevW1/808Q/Ap33RsnJAPTw0UkEIIPOoXeJN4Jb+l4YQu3gBkGsxln0fHh8gpLUHFKLGuvAg5RrGmGjATy6ncwqyQTmUKDUOFID8HrDk1TIGYA978KPpiBNH/hy0JkFGuSYogF+aWhVb+j7VmvtG8OXITwutf8pxwqSi9E5OAUTMFyAN8NG5b7ZWMNybdNY4xSmuhJ7dkbmoIgWpwWIPbwNiPFtIvboNiDGHO5STTSDvpABBac5flRQJRllLvSj0POxtcDZHvTBijsoTNntQa8XDOGVLvmW5xrTRR42+og8YkC2+I2S/HrbPjR7VEFG4ImC9lgE7aKMMtK+hIgwp1ZILpsQEqknJHBxfseeSWue6UoT4HmnEM3GKQdIsp49/fI06HT8lONbphF0jTNtJ0CzEDp3s6GHC9dqDvqWnzkH9HbTUxc4O/UNT8gOdCYKztGD9EaqGZYcM+kCs+FaA/99YAqL6SvmNDHkyZFKKwwxMbAqzg15ekCzF3jArOEBTYLYWSmshKDpA4FRElA0jYkgkrhcaJ1xN//30OIQ2x466A97QTtI5ivOIcBXpTWz6uLNVxcjibE2eGuwaHd1e760SjfzYyQVnu0JqhWHLFCclTB+FibAkQCDGaDbFmivAPS+vXAwH+9pF7q/IuDGHXXtR8t+XB1z4qQcTkBwwDGXmmyvJzloEAzQhWJCGAW/zxQjrlovDNNK9iaFYVrBipr1uI5KPV4RS0xs2JN+NqFn3k0Djc1h/zoCnt0dhF6vxJ0+rrLyVg132mqKO90lmT91M3+6i7fvUMt0vVXA90kdXX9y63SdbETV3/ldc75cx58UZNCZL4M4e1oOcqcxas5m1ZxsSs1TvHpGomOeABpQHM849f2hGa56Hb6PvDA2U2HTXLievXQKsnpax16e3jp7wZmk12svH9Moo9xcnhZEMJovAhuyjCEeNcVaLjm2dTnuVWxlYrgts5a2FyV+HHihLRAncJyqNPLPh2NOUyWB1Fp6XjLbL2fse1SMin/0hoP4l1qxcXbL9wh5jREyIQ7R0tVwlikqydIB8m7hgfQqbKNKgfarFGh/GQWaid6qFKhhMdxmnGQVwgdVCB/UR/igcQiXh4ebQbictmUaPKGvUyj79cibv373d5UwhU/xN+kwoakGuDFRmqkruMbr5XLlksws5aBCksf1JHncZEliOEFd4YJvUhK7HOsbK8vlxmye1XFzz24LL5frHrKZh9rz2zD/JNc9Y7dwpuB51dBWt8bQVrd5Ucy1zRQs5xBe1HEIL26LQ9CbHcMtg75bgP6wDvSH36FfI/Qv60D/8rZAj12HCEa0EhAqANdhbJOSKCeXh9bNvyyI5KQerTxpmqd3HTmNbZ6agZlgTGpKhZQac7GZfuCaGOZJQY6v6pjWq9WCA45tKqTLrirHG+DRSkd9MzN6VYD/bD78M6O+Zyta0foEUGZI7jUM/B6uNqr0wsrhrMir6o8qvbjSqNJae5utKXdJIPCoKhAIagQCQdO6hzwQII4kUjIllMs5pZw2ISwICli/rqO4r5ugsuvx5O5U1iW59qzLZ9YYcteQ5l6+LkjrdL60pueXTtfe5/5/nlgSzNGCYGHG3l2zRnF2Yok6lLtMgfpopYXARG4g87KqezqtmvQ4rT8veXqVecnv2lOeuMvMVAIDz2KUCEuytPqseV6yKq30tKozfmMvvK3TT7xp0ISZdNjElCTnW0wrfdsgGIDeTcwbMrHREYEqL/Wmyku9qU+i3zRuarZc07Y7+f22CuG39RF+2ziEy5V4m5PfmQa/qZgy/VJvbOvLdY+KzJsxVY7E48lvpW7b5HdmKW8rJNmrJ8legyVJqCPVeO4b43kDk82W5HIzXb/VcXK/3ZaQljiYaVdKCdEJxjrNfLumxQu/VXHJfo2BnX5TBnYKixeYQ7SCDp5BEEiAmheW5296ZGcu+E8t+MVM7bAG+GFTwM9H1Wxq/Te7idOW4a4KmfoW6bCA9Ls6Duhdg/gVlg7WxIxyuFhoLm1yocqgV2v1IA8i3yskV88iedz74x9mD475gIajvh9NDGCM7zJPg3cZ5W/kMK0xFYxr4DMSM7q8BuParTmtas2CQbyK1pzOb42GkGNtrXkZdIYlXe3+eHByTtbghzrK/6FBOYP54p1F4QReSd0rIH0zCWkVF/1YB9KPzWGiyuHu5B+5fXyzFNf9Aqaf6mD6qYFqupDYrVdPJ0YBp3D8XAfHz03XzQ2BWh6BfrKYfihg+nu92PP31VDN95laL1WeGURYcm6f3Jhws8j2HhzhOjZgit+SkBOkK6gmlCrNtDK7b21wPG5u0GNArSDjUY2wJ2pK2FNYSMzAsrjQlHOptYk6mxIEeRb3qID7w3pm8XBls9hEIKS4gzE1o2WGXDOZb8JBNhIKlSZ+jVU6A3IK3K/zoZ1J/vp6zR1E6UxuSYx/PSuBx/67lnge5uJ5UCKeb7XE8+1miOd6pPNwkXTKudWHauHE9dhV3Bh2lQtCFHtd00UUT99Y4jWXL5f5w6SeTJMbIlPtaK4UdxUj0AeZpeo3SKRgvhG8maGYGazv/fMEXjO16x9/Hw2SX37Cf0boc+Cf+MgLUcfvo270x79CP0RvRuFpcgeN+nA2RE+iUdjJBsLCIDzxegmcjxFxxhuaxujbyPwqwB//SLc3dX78N+z+8hOZfX40SKafHvjo6R//hALmeXTO89IXThs5rVwJtGpnuolXGC3YjDdPN7mO/Sg4HpMqu+O1u5PrAy74X0tEMaGYEs2x0tTlOtVW5iihJZdEgs5C7Ewn+X5ds/5ozfpzwahbixjkrFm3yjjkNRn2bCS8S7BDJocc8I3yz+XGTKeM+QTdB4PkqN1f3lZoE7nPjA1AmCuZFJgLxSAAY9Iawa7rUMqIpFxJIRRlSleZQTl6p1PoPTn6fHRx1DsKjsKjzpF/FB0RwNNeQz+jfBYAvmbn2v3/+a8MaLQE0uvPBl4H1F4rHvRGif+uHfl+mP+4Sgo7VdaCuJ2mWYxnewGeuATP9sp4bmBn2w0DajI/LKAFSl0OKJ8CdP524gi68p+hu723vO3zG9RPGugyX+uWOwlHcqKUWQDIXE00phmvw8I1Ow1pzTjFrqrnIsSUBHKw8T2EdtGxH4N7L6NGKfVBxT/ZPZbvLC8n0UxNLwhAEUGYoFJhjN00ITuNWoG3AH02idecgBBkPQnIUgmQVAJnXhSYnfi3IQTZSPc9IwPhcECbM84EhC2CjkXAFVMCp5PU1DU58cvQxbIMgaqtajJvvkySa1W2wES26/XlDMxv31KLOaryB5Zp31qzCMrp/tyBs3Zdyt9ePGx8qa1X70VeHx/HfpJOdWUb9VNWajRkNh4oZmWCsWgFob2kEryW1vnymJuwXrzcV6opX7nvm98OeTA67kKJGrRA3SBasCh8BlagCOMEAmgqFBAvnsfPEsgAZUAOhGSqZp+Um/Ik2v/7H/+JPs4PIX6a9gToLwis589TBPi/6wQUG1omtl2BzQtARMaXx78otCgAWVouuEwu7fXIZWPbijZGMNoG4FwX7WXODOOjdXQV1z7nzvNl+mwLC9j2bwVkePyrROvCbIn5wUc5zdkvoTmjRTRnds/mlSfH156ZoGdozHZnAx8tmg1ctG9zGee0/vKIzBdJ6d7NRyuO9efjl7mj/b5M2i6Txq5yKMGMKOFCKEJM4sX0MmlurkO4whTHRGtXb2CR/XJbix3US3A5WNWXriftC5f7UxPEreZRzSojCbE8iIqoJbMnN5D5dZD72aKAOosENJX71WmOjy2sOKLwxaw1YpgSLuEvW93nrs8kOiXO9HE9o3h8+40iTxnbxurksTE8LhGNX3dsxW+QRdAZ2sGJw13JXC2p+dn4GzR0stiu/BLhPalnV0+ubyZ8Gza1xV9dGZvUkxKpnNXk8WfXnqDQ6Fy/g5XZ/ZiN2036SkR1vEhU0/z++KqS+s7sp5m9ko4C83W1kJgyxsSSxH5L2x/NaFCRTD7N/cCzep746aoMZyPre8nUFjVSr5m3z/2NgUYBwaZ2klnznlDLOa2xRpW5q+f1tOx5o8At17LtboT0bB66L+qh+6JR6Jap7ja3QHqeI/u0BNlu3SCju4mOdllwC7O0haxNih2CJ34CaO4sbbM3zymX5ouZfm16q/a60jy5TmkuzsGlwiGXOyG5TM8bR2m2NKv83qfqge5PGcep5fsub2qOXDFddq/q1ZZrV2I7xqKyZzmsh+5hM3HdzBYNFb8TkcM5pZ4zbojWdUOL8srL++tVw+zLtCBsV4ryUsDxYgdFHbnUdlJNWRewbMbeESlG5FNZDwtm3+Yn7ZHrzdo7LhtvsC94vMAdVLTrGG+0RXPTV8iCNHpalkaf3bp6Nv2kIFf3hmYj9+2uUhDSrVqlcAXbGNTTmsEW9X/BzEPZMOnJorn1ov8uUYRlAq6rj5MuTtyk0uEuJ5oIwSWEt3hDk3HX6q8LMgwWEZtZnQyONuvDrmBdX+q25cuG21Luj3Hp0gO68uKPfLlC3aUHV6WoG3LKs6m22NFUEFcJyhnBBON88YEiLmdcaQlXta5cq1ouBL1ENudUj/gTKAv6CwIKunoKp24m4mtJ3hQ8o8hKLycBNiWBOotLWRMn22Ynvd6XxhEi63Pme73SH2o7ogWH975OTPr+OjMy1pn2OR4lcB3qSkIVl4QQSTRl6xnnB0DDGNBIO2Zz3PUHXb8Veb/+H1BLBwi7ccCl5BIAAKSgAABQSwECFAAUAAgICAA5c11BRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIADlzXUG7ccCl5BIAAKSgAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAfBMAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" />
| |
|
| |
|
| <br><br><br>
| | [https://ggbm.at/mpQGZVpe GeoGebra Applet "Volumenvergleich von Zylindern (1) + (2)"] |
|
| |
|
| <ggb_applet width="1584" height="717" version="4.0" ggbBase64="UEsDBBQACAgIAPRyXUEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICAD0cl1BAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1dWVcbSZZ+7v4V2cw5dXrOFOnYlyq7+2B2jME2YPfw4iOkRMgISZZSgH3658wvmId5mqfpPzY3chFIGSkpEi0pCpfLWnJTfHe/cePG67/f3zS926Dba7Rbb9awj9a8oFVt1xqt+pu1fni5rtb+/rc/v64H7Xpw0a14l+3uTSV8s8bMmY3am7UauWRVJS7Wq0qqdaYVXa/gKlq/rFUqktDLC00qa55332v81mofVW6CXqdSDU6qV8FN5bBdrYTRg6/CsPPbq1d3d3d++ii/3a2/qtcv/Ptebc2Dn9nqvVlL3vwGtxu66I5GpxOE8Kt/vD+Mb7/eaPXCSqsarHlmCP3G3/78p9d3jVatfefdNWrhFQxYIBjHVdCoX8GglIAPr8xZHUCkE1TDxm3Qg2sffYwGHd501qLTKi1z/E/xO685GM+aV2vcNmpB980a8gnHSvI1r91tBK0wOQMnT3qV3uP1bSO4i29m3kXPYWte2G43LyrmPt4//+kRRJD3q3nB8QuBFyHiQyj+DtH4hcQvLH7h8TksvpzFp7L4HBafw+iad9voNS6awZu1y0qzB8A1WpddINrgcy/80Qyi35N88TBm/CuMqdf4CSdTg2qMNHyP0K/mf4D6V4YShB8NEj96atjtOz40fSTmik3/TPKkkdL0oQzR7DMJzxmnGPPQeODTDfQRtvCo6G/0f+aJdNwwR58Yf37aAwVbyBBfv0pl5XUiHl7vypybsE8Y3PSMwFDtcW34HnschENIYHPuYQ0vknggDh7mHuPwEStPmFfpUQkHmEc95ZnzMPUi6eAK/mEyupnwONzMfCtBKD0MD2Iepx6OhIp5IEpeJJggpITCGZx7HC4yj8fE3IIKjwn4RJXH4DcamZQYTqRwIXyGxxOPYo+ai7H0iPCEuR9mRtaFMj8dbkk8gTyBzQ1BrEGkY3GG85VHzWhEAlej1emHQxBVb2rp27DdGdACzgaF9KDsYgU1pAv/9LpZuQiaYB9ODCU977bSNPIUPeiy3Qq9lIgi/q7erXSuGtXeSRCGcFXP+1a5rRxWwuB+B87upc+Ozq22W70P3Xa42W72b1o9z6u2m2jwm9tN/Og9Gfxq+EAfHWCPD/BHB8Sj99L63DYc8fq9AJ7f7vbS0yu12r4540E1AJLHreaPt92gct1pN4aH8fpVZGpeB/1qs1FrVFqfgVnNUwwu3sDyRPoqtTxC6fSXtLu1kx89YGHv/jzotkEAsK81IlxSSjFSAizJj/gI1cyXlAtEKCKCYAU/rVoxskfgGi4RZ4JJrRCl5iL7MU5Y/OjgdkCiyn3wMNp6tzFgFvN+v/e23awNDkfj36x0wn43chpAI3bNoDZa9WYQ8UikbsEiV68v2vcnMXPQ+F6nPzrwCcU/4KIe4e6BbiAcfnA9eb2IX6NzzC8bnIWic1B0Bkq5rVGbfBdg3/inJSPF6SgJSh/T6EUaDa0lcpNqK8P8xr73W43wMP0QNqrXyVBxfMFR/+YieGAhc8JWI/ZG4Cn+6GPwXB9jxgYOSS/8R+Limff/+ej96VUQVoyrwgnlWknJ4V+ilYr5eYSTX18H3VbQTAQHOKbf7vdiPfBIpmpBtXEDH4cURMUwxRmMKf62FtS7QXJ+pRm5fTFZoqPosUhkvo5utdNt3+y3bk+B40Z+wOtX6a983at2Gx3D2N4FGJvr4IF3YewVsFW1x9cZSQc0q8YmAaChQfuz0UdBC/xkeGajeuXdwrHzH8BG4OK1vtKvl437RtANA+/44ltwHRql0Q+v2sCDm1ddABj4zTsJK304/abSasGTQQECSY2aaAZw69ALI1GIpGlA/43IyzSE9tpw42o4yiCP8IYTrIIRMX+l2bmKCJyA16z8CLpDcEY3fN+ujYIMNIyQAI3UidmuEwQxx8a/GN504HaR7A+pVKBaz7t/syYNl/14s7Zu+NH7GbNd7GWbwRqFED+TPv52hN7AhDFOExB7+xwQw2SRkG0+C8hAd2HBiMCIag3/yhhADF9rTrRkEjMlNZEzwbPavgE5rnmtyLPdbjYbHfhND75WBRnh9SrYcKRXIQblGMB+mB6vxjdNbpUhEuihRnVAg2qWSInDPgWNMKcxlRB7RCXiRiVQcUEt/iZ68oghDcHHu4ZIthd5AGFi16M3e41aLYj8+9jPaNSNKq2G4GJ53j1K7NAPFLOO9zP95h7QW4+++oGTr37iR7QDpuk27r0NZNIRVCnOOUNCCy05UHnDnIpGDoBHvAHEkIr5WmkMPhMHr8qcTZOnb4D7uM6wLzQmUlABpxAJ/ssGN/gpX0qJwQvDVFPgq2RE31sxCL3YODduOs1GtRGO55pDwC6PZUZ5pTKeVwwZBqxQmYE8o+LS/CCTKNFiPFViD/eysQ2ZwDaFQN5vheAfAQgjSFdjpCsZpHfiA7vjAR/WoDsFETfhcj1+uYhfng668DWDUIEgrolGQqrFGZLdEsFgTCgHcyA1QxJpStlscRjmsg8RDsMclmWtLRee2ioIJiZxzBO9FrbMeHaWmS3Sl9l+Dr4MG9WbM+XVz5HlHWHWrVjrbWd4tj+eZ2MzPkC3XzbTIxMIn2R5HgWgie2pViDW60FAHJ8AAXc3jHSAF9x3BoKeR4HTbqXVa0IAaLdJ/ayn+Eul0+797uQvJpe8eI2z8xohipA+RBGKcKG1RGRKt3Gdm5QbI+A6IsoUhCFP8WjyuGcnj3t2puGeEYcmj3tK5tbMR0PmIbybh/CuO8K7pUM4x2OaD8QnQd18b2fhRww7BPPFeIB7yT1T7C5mr/wcwbUqvwfE19PMGEowZsoXBGHCGOagKSTLpKsd9OUY5RKh2jQeyCA8Ao8lm8K9DoKOydAftyKRMHP/w6NxCm6380KumkNwWyubh5HKxzrhi49up4s7DlwU08FziTsInnXgMY0KS2zEbo4Ku3RTYZcrp8IUuE5SK8m5YlpwSldWg00nW0cusnW0VNmaYYTKfawQQlgxBv6sKTOZn5wdd8Ordr3dqjQtNuUoz6Y0HGxKoyw2ZZ2PSBPYFA04I00IYSStqBhvX/DiDcwHFyH4MAntBz1TahkA+6Ko4kRyBsIgQdMtOMHYyNBhz4UOe89bGc0nbrGooL08FRQ4qKCgLCpo1K1dhlebN2fTiJGuZZA+duH741LF3NrnwLtMYEwwAscpAh+TLPxz9FkTI3qcwfWbm7f6rSxMnPFKqfCJABVBNMZUI0LZfHh6SW7ptwzlTlwk4qRYlJFW18WE47iEVgD5BHMhuRCECEG5EmpRMyqJUJ1kSPNzPGlGZlR+zoI2M7UMZBRTuYQZlqPxFJkww/IzQ5RkuuQrGU8c6xwLXDRjGs1tjmWSalv+HAuVwF8mwS8F11qY4uQpJ1kI8Tk2qWtl1rUIuOlTfBCLo3eS5+i1HBy9VllsZCZ/CcSTisJfMJEUSz02dbOwbGaQQXvfxbTtP5ds5qCIdj5xzXTQH7pAf/hc4ktwHhkE+EwwLDjFlIl5UsLuou/HuucwQ5K6m4teL5v6gQAoA67BlEmfIWomfBURxt14Vg57PUPH9y6i9f4p0wLRdMDTyDiTgm0+X41mdcoTMXqfgf/WySm/XTL+DyiqkUB3sV74/pO88NtcLxwX8cLxrInyB650wqB4fY0lpghxpRAfdcKl8KXWEmtwwbVEphxn9gXyEyqdsvyzMx3/WGudbPyzvLwgGyl3kvOcXJhQ75TFebcIzrslxJmgZVeJZ5PZ71xAfVfCyTTkP6lcY3EBThb7jy7Yf3wuAQ6Zb8G5PaJ5FyuXjxkaXLlFNFdli2joIKEyt6mzJUUtVxlafXKRl0/L8ppz0jAF9dQSVmccxLLyKYP/nVPYcleasIUudXnGQcGwZeDARNS4y1Dj2iVsuX4JV2YWrjBGuE8lwUjDH0kyCzOU9k0xouKKEQhnonhmcQszJvHNqYsWPS2R+4ylNUxZ8KqMSfCeucB7ViJ4CV3+ioxhcE8z4DbdvLXmkk3QtOXMqROHMRpZkvEERblcj85O4LOhevWvOEPgGzcC35SbwINptAcvnYnnUrFumbP+kKcUO+PJOjRn3SlLiJUVT658ZTwBIjURHC98yjqvVLET497K4P7ZxRh9LpExklr6XJnuYAo8LI514sBzpgRTpl6AEG5WnJhyu9lWLVpjooSzP2cQ/u4UE30vC28jcKU0l5woqohi1DSMLUu11YeZBEzfM6TqugRM3Zcqq9nN7zAJ96UImXULHHz4TJWVAn4UQitKhcIM6VlVWQE/dQEkk4VJA5rgPgQOiRjtl+/9dvj7SfWq1QjDq3/9z1XgXX3txd9GdxpmkBAuXRu+z4x5ZBbeR9QUtRd0G5cPDUSjJphoLUULZ+QuMnfIZ1SZQjhCIEZFTCSVJ8hX8AVDCrwVrZgwP/8hIMgX1I1uUMmRUZIRzsvmv/7LNO2MT5hQGNnq38AAH4R19GJzb4Cln8DFfIII1xghAYw0iLunUbDYeYjdvKFNUD85Y+oubjDTrfr54uJSfHkukxZ5q37APdGYQ6QGcTMm8yj3Hrsg8Uts67JU6jk43L2yOCXr6aTG+sMyd+0z46gISQXYDjGnlRRuQtHLwH3uIhTnz0UoID7SVAksFRWMgcu+OKmYjiwbbjUDG4WrBUpHGpAb8LY4V0hJFMVKi6ONPfVzHquqDUvSJ3RL+oRl0VeDqlLsa0zBOaWIggfFeNL11RABnFoMEgJgm7UDc1FeS5qfDTN0fOsmbm+fkbgJ39SmgWsMtKaM4AWqQmu+IpG2txZp60+i0miXvcJkmrnAYe0roUDKpATFphlZYjXqecEsRdLVy0KYNDiiLnmKh4ueFIum3VtepnjjKV4smY+oRgr+4UxnpnhBlEG0GSMKNL4STC6hItXGQzvTrSy016RaVhYubzZS+CYTRLmikkLopcUSa1JtSO8WQXq3hEhT8F7AQZRYYhXNTM21tYjVWj0w4ND0YDZLdOtou27LY7u4j00GjStga6wEl0u0XSNaomiJSUKuW4t0HLi5ggelqtNerERM1/Ro0w3QzefjW9O0fG+pdfJbbvhvPUP8F1iCupnO4m1ZdMudoxG4K48RWG6j8IEOKTq1SpP6Dlvw4riMrugCupeAxRqwmPYUPgZbxagG94Jn9pjJCVgWW5NK8vln202/bpfKYcgJVpZTmToG5B3HtYqlAjnHK1tkfep2apZ2ciOUyiSIR7PZlSdaJ2w2Bniqn5AtWUwDk3UA2xdaEY6UwEIgsbq9EXKKjlOi5oedF65EvSg5UQmhPuOgqQiimGtMpur1WkqiWsMnW77Gcf3w83Hgc6wT8QXRTComiDTFrGRRsa2FOHtuxNmbTJxVaetrpw3yTYpIac01F3BgNttIjm1dNZMgqQx4cm6q1ThBgCtSLN2YE2GqtQRm51gA3nwO3L7Z6Fb7N1X4txlsdKvjneD9yOyQAe8PyUNtqmiqA+Hdw1YV84ioZlGQWJaIKjq4kZ5lgiZFia8E5YQTQZnMxEwQMmnGKMOcgc8J/BTHTMg3i88QB+NJsKDwfkmGcGyrhmciz2YLLEapplxq8ELjrDn2ORWMcqG4aYauzPKABUvzXuo1vkvleNcix4G7HAcvcuwqxwIpnwsqNWGCYpVt4kmYb6pyiEIEjjNk2r5F2Q/sMzPFywjGENsQrksoyYfPRJLBMoOqpBhJ+MuQSJZWSYjpCSbgAzHNFFm8Xd5NJfkwleRtiyRfukvy5YskO1tkxn1wdyH8FRycNW2zyJQQzSUGs0zMHiWxIFPjRkuqQb6p2TBRqFIEp3m5uoH1sM2dvncLht6XI1KdmKibT0wzHd7vxuF95Ib3UdHgc2bq+BHUxAftCRATk/YXmizOPcpNQ4+D+tgN6uMVYe1FpFLGG7H3KepHqRE7tsBfdzdi9Rcj5mzElPSZ0mDFKIfgRWWKB4n2lem0QTV4omDqJM9xRxUvtRUbK+of3ET9w4uoT8T7cBzeH93w/rj8qGIIa4G5Wd/LCdMEEF9ccPCEIrcTN8hPVmE6dcEFtvvjWPrUDd/TsrG0QGADGMKcK7nIPHShqOPMDeyzFdHXi4g6xrtmJ4N2VqlrdmaB/9rdNbt+cc1cXTOMOfOFMi3EFUWKZlOFlPnIRFSSEWW6z6TN+zJJ/1J4ZnkNgeopz2VbAr1PLdpHt6UL70u3aAFCXsmkJKBkB9OmoxuwzUa9jnekyoTLUeUoQiJ6/Rm/zk7R5bHbdT67HaXsduzGbkfPGtbxSY+CO7ytwsCnqP0eqWM8sBjLlmMFeOuplnIOJeDLWfmzO93Kn2kIc2QplOtPEvLM2uKiUj7z0vxcTl81ury3rptzo8tteegCl2KhEUUcIilCkCSCladX3ZR0m3Jhxa2FdIHbLqHBy/6gM1xWQaXgpvpZmyofOBvbllVo8DNNLCE1YySdkJzt/qBT8k/f1ljNjX8uX/hnhvwTGZMhjom/4Y/sSzGOeN+odSzFtUlrgN0MG3xyc78/FWUDNJRZmFFuJ962/uEPny5ViWeaPfuUGth+BtwTN3BPVgDcSctqimE73VrbUzc4Tws7K6UrB2fMJ0IJKQgSCmu98BVOJymTn1rXNk2gS3ZtU1FjgtgcW6RadlFivnyEu9LJ2idJfcWoKUiiDGnNplr7REq5TmZsH8nTlOzZxgMXk4g+1EvyojyBwzofibQJwT59TE31BN9ipv3bKzH4FxaZO3PThWelSpthjIQvTfjGsURMy2SOkQ9IMtvW7XadNjDcZxZ8r1x12tWq6rS495wAc08l5YRhKqiWcnU1mjUZcjbOgP10TIP8LDutpY/Nnj1ATykQRohsr2O+xA4TZ5MSIVaanY4T0IYjzRplp9l6PtHWl0O100lUs7Q5D/J7uAfFurcHC+zbPqGz3s/M0NJqIOZijB8uKo9JFiN7qCn7xOk8yiTyvJ9W4npaOGpzUjPM0a5XBdtgrt7UWQEwt9zA3HoBcwyY225gbv9xwBxfDXWclgp8TKuhdiwTvFfu1VBXL9VQ7tVQQpo9X7iiSEKMRoWtGoohZXqEMFMwJcu93CpPji/z61MOU9/zi1v942GpAu1F1qd8KSpoqzBw92a1hxbjcOcYs9yVJ2u23DKIJzamzfQpzJKm7jYdWn+ZDl2J6dApd8PObgr4yU3tfyrVGg7MfaU5GG/KKMYaY7a4aG7KnEB7Er6j2YB2gvBy8wCji3+yA/vglpj/UCp/wbSdombzJqWx8eLQAhlnSsxttSznbpiflwrzUcs6d3G8zE/RXRZL0V0uMEVnKxXI7nO34xaG79jC8NUsFbDvSKh8SanABOI5gjhHdNE7Eu6kzleWVt+cZpK/lccntuxLyKgPQS8wPdUCEcnxE/yyme1L+M0i8LtuArL7fATETLNoKQXGJsNB0imWRUjItMTZcyPO3vMhDhU+N1viqShsEKDDFkcde5XAXqq4EokZWZ3pWCVwXR7tNVBeZi9VLjkiEJgpbfZ0TpoBc+kTiRgyHQ0A8jntsbqkXsDXFrnbd5O7/Re5m99qr1Ts9i1i13TMozXLI3U2YVveqq+U3x9leO87XXiW4aa0jDa4D4Ebogt++d5vh79fxS/RpcO4h3Du2vCFxbJkc625GNngnjGfm+ZykmKzT6fCSbMsSoSGWBdrZnbuG+qVVXh/x6ZF66TZSe6SgHy4qBDAUSP5h94WiC0iEVn+7VJMMaJPQQFykE+ltcqs65HI10Jirk2TfA28scgNHh+InrPgoOOWxe4UzWK/sI+VfTRhpscep1gwM21Kp2Wf2W63kzfd2UlzaNmlFQepuX3n5gIdFHaB5tL9QfgMUUKZxhwrpZP05awWSozvq10mIAwbYgzMJLUQCPTZHBeM5HHbiLLKriA4THnuvRvPHZYK6hyem1m/rPG9V8qEhJ3p5tQ4LGed4yhPjbTCc+Kzj0Vrs8ZZx+J8ZhYUPwocpmzLVmw9Xg6671J0DyzofnJD99MKoDufxY72PNPHFNtPFmxvXPNMN0+tT5hX1dtQvfvIOixJfIkIx1prbJoXr/CquveNbjeT0xg4WTeWKPDETXxOSq366TwdDiu2h+OwPXfD9nwVsDWaf/gPW1hOfMDIhxZd1XLVVa3yZOeyG+Jx5itCTEIUCUoIpcXTcyVMgrcswnLkJixHzyoJbnPliQ/GSJtyBgZSiKI+Q3N27I8Lg/pYJMoAKMKCGEwF4lLIpH0zAzSZFhxhsPMYL7z16kB/HUdvyIDphwTh+1TJtKHFBt/nkVCbhdtl1VesFIsNmKYgYBSD2GkNOjaz3Rr45pwz0/+eY4G51IPFBoJRzTHRkirgJbokNTu+vO95CDL3wfkwy1MZQYA1T7tWY6EUkEVpypAh0cJF+SgV5Q+pKNt8kq67KHdfRNlZlDmjvpZYC8JAs4PQZkRZ+0wiraQE5c+UIIkoIx8PiTJR5eij7B7Gnbp5T6erEGosMIw7HoftmRu2Z8vXvUPQKtM2nDBpJpul3RUyu98tBuijcUB/dgP6czlCgIl8nHHkF26tTlPUz1Jr9dlirXru1qr3Yq3crRWH8IRyaayRJjS7zy9YK4hbCIL4H2GFBM9xPEmJjdVYOf/iJudfXuR8PNgfxoG94dYkZKNwe5D5WC/NlDZYgn+Hqc7x/1Up0r1v3ZB+W6pGLEtN9463Xl9S0A1vRtYrQXoI/dDdeoUv1ss9bSIg1gIThijmhKNsiwblm6Q1lpoJyaQqe6iVV0bSTYuWsj0aNiM2xMaJclqsu1kqgafcl0RpLQVSYLY0XtqWNZ//OB0c8rgtzOe2rZTb9t3My1apuI0Rs/EZMjvQEY3FYDe0xXPbvg2X58ltefW8m/lF4Ztx9ZyTWksuKY3XCPGTNs2AlOZaaUZZ6jVyrDnYHyYxA41H5rGa3DbbOVRoP9K1y0mktwuLdOnmPBnyTYsncDkFlmYNxCC1D2qASEokoUKoxW5IuZ2qWkvDRcdWi+Wg1ES8kc+VWWlHlTZ7UpK57B+83Ww2Or2MEkrB3kq9+h2LV1+dlCoYWZ5StLrvj9Efh/oQREspOeaKEiwYTdx7oX2luMScazDFisfOPpMoYhCOqOnabJYsj243g32KmNaCCWPEUbqugApfAFthRogx+WqKOVJ3p+n7g9MU8U+2b9+um9TulsplWo4n2psI6p4bqHt/IFDtmm431XR74zRdzU3T1Zau6Waj1GKCpG+GlFp8KH2Tp9Pill3pWUNtveI3M2zrZelqU7VMpCTtaaoTCJrT1aZKs11tuFm6hc1OwAz0Ns1StWBXG8uAavkDqhUbUC0zoAEZZjCEafYg/GjdG3LCaDJ7Q85iWncm5aIrsTfk1HvEZdktcFOFwdJVYamdvtI0RbS26MtVNkExZRNYtOeS2/XZWPzAzYk6KLUTtYja/8GuOSfWTTkmJOJHa/8bZe3OPWadkhDDO+NN1RennMuUJu5peJsh8bnbXMt5UQLHqiCKZGdlrrEc2dJQLmO/yPO06exdBtu3bn0s3z5tv8iZYkuQFdv5rKCcvBWnZe+ADTdwN0qwgnKobRAViiIqpULKdIpYBuuejMN30w3fzaXvxzQR3UUu/91Iod20mNVvrmb1W+F21HPh3uxSX8R9LhU2C+uESOvnVsOC2jtkkaEOWZ/bTfCKIYDo1ptBo3rl3cLZ5z9ggLWg2/L+Sv/9t+l7aD1JyT9ZSqze0WUbfm4P3P7LAVv1QCxMAnstJQTORK1pz1RuFpEwwgjhSioWFzhh5htWgCNmGT6hZGhZ2GQCdIcIsPH15Gv169XX1tfG1xD+I94bLz7i/YeXRChdeJt8V735v/9OCOJNQZHurMPcWdBkND3wKdXR0T2OLy97QRj1fUwsRyamsuOapAnIWHixBd70wsIoD568AmAP7QP3VMghdB4HNrWAHdDCMAczT9rMA+CD2UBbHQ8ts/FxcWirKwHtZg600g3ay/Eqwsa1l8WVw+VKqIXzr2Qs105p2wJ3aIPi0AYrAe3hbKCtuSuEWnGFUFsJhbCboxDWsRu2fAjarQDce2+jf1mHMxzc34IdTpfi/qIJ3i/yMZVIMiSw4vBWxzoWY59hTQXDlHDENXdzfcUQzl+CJjCpB4HGIOLwLoJeI/wZtLxapefFIUngJUHK3723Qb37r/+FE+GiiEat8K7dDf/yy79h9PtRHy6E6372vVojgDvdBfWmub7lbce/K/jL9MQUz4uYjGslsaASqMc0iiMZ7WtT0YMoppRIJp7YOXiQ1MoWw225pVy2npYvTFMCM6qE0yMJQ26vRB5fHDrb/NagB1sW6m03qLdLsKJlUne7pUJ9nr/12o4b1DslyoJjs+jGQE0UVUQxVgKm3hg3/bnrhvVuqZLi005/zglP2zaSe2547r3g+Zg/bTtyOOG5/wfC0z6PcBJjuW3Bsuk6i9B86uT8fBy2R/MKxJeSc9C3AvQrURqz7XWctNagpiE/RxhhDH61TtbLrksf9LKGvwhRqole4dl7OwccpW1ksxxw48oBN4U5YK4beGQ3MWI+NW1jFQZuAFZQ8ZJ/5QsaNRXD2Hjjcqrd2MpJ67Gb6w1WwwcZkncmkXxoc71O4XnDmddWxnvqPZozxIqYboJYmv1zNLhWZBpquhPTVd62U/u1ZSkm/+4qcd/LrnO5bxYvYY4JxYRLRR80rm9WrCBOmERYUcSSfcSQL4wImpoQ0+JIab26YjiBBfYsLNB1ZYFu2VmgYNlzOSk60S21bfJ84OaWHpTKLTXVLooTJMzSM9CoybrcOQWp9pSlwwxn+ysunG9fiXT7B9eZDOC6Vg/uFwmD+VwP2vXgolv52/8DUEsHCIndY6egHwAASUcBAFBLAQIUABQACAgIAPRyXUFFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAICAgA9HJdQYndY6egHwAASUcBAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAA4IAAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /> | | <br> |
| | |
| | [https://ggbm.at/W9hf8qwn GeoGebra Applet "Volumenvergleich von Zylindern (3)"] |
| | |
| | <br> |
|
| |
|
| <br><br><br>
| |
| <span style="color:blue">'''Zurück zur Ausgangsfrage:'''</span> <br> | | <span style="color:blue">'''Zurück zur Ausgangsfrage:'''</span> <br> |
|
| |
|
| Zeile 65: |
Zeile 67: |
| }} | | }} |
|
| |
|
| <ggb_applet width="1584" height="717" version="4.0" ggbBase64="UEsDBBQACAgIAM6sXkEAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgICADOrF5BAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO192XbbWHb2decp8Ctr9U2a8JmHbruzJNmyJbtsl+1yJXWjxQEiIVGkzEEeVh4nL/B31spVrlL3eabsA+CABAGSAAcQYKerqyiSGIj9nT2ePTz952/3fefRG4394eDZCXbRieMN2sOOP+g+O5lObhrq5J//+g9Pu96w67VGTedmOLpvTp6dMHOk33l2Qgm7EazDG+2btm4w0lYNpQhuNBnHbd1RrNVqnTjOt7H/58HwbfPeGz80297Hds+7b74ZtpuT4Ma9yeThz0+efP361bW3coej7pNut+V+G3dOHPiZg/Gzk+iPP8PlEid9pcHhBCH85F9+ehNevuEPxpPmoO2dOOYRpv5f/+EPT7/6g87wq/PV70x68MACwXP0PL/bg4dSAt48MUc9AEUevPbEf/TGcO7c2+ChJ/cPJ8FhzYH5/g/hX04/fp4Tp+M/+h1v9OwEuYRjJfmJMxz53mASHYGjOz2x13j66Htfw4uZv4L7sBNnMhz2W01zHeff/s0hiCDnT+YFhy8EXoQIv0LhZ4iGLyR8YeELD49h4eksPJSFx7DwGEZPnEd/7Lf63rOTm2Z/DITzBzcjAC1+P55873vB74k+mD0z/hM809j/AQdTQ9WQ0vA5Qn8y/wKp/8RQROG5h8Rzd52MpgVvam+JuWL570m2elJqb8oQTd+T8CXPKVbcNHzwfA86R1u4VfD/4N/UHemqx1y8Y/h+uxsKVsojPn1ieeVpxB7OuGeOjZbPxLsfG4ah2uHarHvscGAOIWGZcwdreJHEAXZwMHcYh7dYOcK8SodK+II51FGOOQ5TJ+AOruA/TAYXEw6Hi5lPJTClg+FGzOHUwQFTMQdYyQkYE5iUUDiCc4fDSeb2mJhLUOEwAe+ochj8RsOTEsOBFE6E93B74lDsUHMylg4RjjDXw8zwulDmp8MliSOQI7C5ILA1sHTIznC8cqh5GhGRyx88TCcJErXvO/bPyfAhxgKOBoE0E3ahgErIwj887TdbXh/0w0eDpOM8NvuGI4Ib3QwHE8eCKMLPuqPmQ89vjz96kwmcNXZum4/NN82J9+0Cjh7bewfHtoeD8fvRcHI+7E/vB2PHaQ/7KP7Nwz6e+5vEvxre0Lkv2PwXfO4LMfe3zLzvEL5xpmMP7j8cje3hzU7n0hwxEw1AyXeD/vezkde8exj6ycd4+iRQNU+9abvvd/zm4DMsVnMXQxcn1jyBvLKaRyhtf8lw1Pn4fQxL2Pn2mzcaPjuR0lVKc8y4loQJ4Onv4ReUK5dhxbHmTFPKNVxw3G4a3qPa1QorKhWWQiIt4aTMr3B4W+8xhqf5zZs9aXfkxwvF/H05Phv2O/HXwbOfNx8m01FgMIA0HJkHOh10+16wPgJRC9q4fdcafvsYLgwaXuvT9wd4h8If0OoGNHdALhAOurIbvbbC1+AY88vio1BwDAqOQHal+Z31V4GlG/606EmxfUqC7G38cSDN0EnEM1ZSmYVvdPt04E/e2DcTv30XPSoOT3g7vW95s+VjDnjuh5YI3MVdvA3e623Ms4ExMp78izFF+Enw97/O/f2p502awXsCS0hJyeG/RCsVruWFVfz0zhsNvH7ENLBipsPpOJQBc/zU8dr+PbwNvyDRA5tF8Qs8U/hpx+uOvOj4Zj8w+UJYgm/RPDukPg4udTEa3l8OHj/Bilv4AU+f2F/5dNwe+Q9mYTstUDR33mztwrM3QU915s8zXA7UbBt9BASdGGp/NrLIG4CNDPf02z3nEb57P/LH8KFzD08zHUwAhnbP9zp9+N4bOS9H00Hnpv/7v8O7gbGYr2/8b743mnjOu9atdzfxroErmtNJbwgr9bwHF4Of6DkfJ80p2Iz3zcEAfh+ISADeCJK+B/eaOJOAYQKei1fJaWCHmuXgDOHS7cniMppDBQ5YYB+MSMwcTrP/0AsWQkTkfvM7PMs82YNLvru5GXsT59uzkwZWIFYChp59/dOws4gVLIWAoCDUHsLV++B54cIPHwn+eIC7BSIkIZUB/LG5U+BtfDd3NKv2R+iohIa6oYaRKwk9FH66sGxgLYeEXEPSswOSlIQElfsmqCiToOcHJCgtaYXKGUHR3gn6/JBMTyKS4n2TlO+apO3hPYjWjjMI3JH3w/737nBwMjOQm8jIU6eJjQxwmsSsXKdJDb1DUk4n9jBQhn2waXB4dDM8uhUe3YYXsEE74e2jm2YgGt7eQhZfMWmjTMB0vht443GwlCeRyRT88crvdLzAbXqSWg6RM7fxasB85XJI4Q36zeuEnwS3XrmYx17XvIt/XzO9nLf9/atXc56fP78SUbQSSbQQaXz9DXDyvgzCU8ahNeffP4DZ4E/iNdY3PHEZGBVeYImk7as7z3sw5vO7wadRczA2JsamxG9VnfiNwFL9HgUnfxhjIGXJ15b67apT3y79hl37DZJv8eNa0L9TffrzpBJs0HzLv5r0T9oxLw5qx+BQpq9EZxd2jHI5F4JJirVUkhNmARWCE00x4wRpLXZjhydtnI/Rck/aOM+tjbNo1firTZZF5vG3gs+GbvbNOTHj4JWMQyqmN/IAGRmr5ykgb4sBeVtpIGMDgEZIihoDGV94AUo/hPI2BeXlNVnnSMyLVHP4RirNxktDNDneHM4ZchjPrIdQvJEl4g3vwCu+ynr00vRJ9KBi/6EwHvki+1AYb4CjFlbmVRCrDLzcxbV5d41Xr03DoDHxzdHb4EMQ2+HaXPTpGnylXRtLFVJcrORdwD+Vvnz3skIxiUiL9hK3yViiL8IF+lNqgXoFlqd3WCU4p+8yLMNA+zFGKSdCIYIJk1yExDXbeZRjKRkxO4FqP6qxEB6Xy0XGlwKIfKkKIlZWsGhBlyMq8i77NJG7BYjcrRqRZ0E2ShFXgmjEsNa07HX9PpDNSYp3U6S+KGKcXRx+Z0mtAmMX0l+7kkusCaNECsWILs/bXWZbeyGffEmB93Kd/ZKE7+WWBsxONPTcHh5xJZYUgSbQCHPNosCCcikRTHBJBGJaER45TUJgLAlXSFGtxA7pfu6P2v1F4WSIFZD9RYrsN6uJ3h4O/PaMohX0TTcSQn7XJBG0J8PR2HG+oSgw8R1ZO8l+8g0HLq/5DtvoBZ5jFeDQkf/NObXHn9qjTsmzE6VdCmtBgokgmZJMwsc0usMpgwtrl2FOOWccuJAiquBzbi5AeLawNKlf/g0AshHr3YRrwEutgRd2ebwqwoEvqsWBpUb2VtHl1UEDqaHe1jljAsglkiFBuSJYK1iJIdGQqyiTSCjOpEaIsnJch1fhKkwr9l4BG6pXVRvKrETNMJUIHAMExK2Ac3CxTCSMClB8VBWKF3PWCAZnjUgpidJCmaz8sgFZJqh7ISqjtI1UyEI6vIG7Mi1lhhtVLqhIUJIMKaQVojZOKQ2fUIIkmEmECLnCF9ljGkrk2l2EiSUvw8SSVylwoqSRyNv2Ap1q8qKDP+CMbvAH6P3e+ihyZjoKKT0dhdMUc5KtTbb8G8JeloWx3c/fz4Y8WGwgPhjHmMDyhXUZhYNcrTXhGrQoFoTBPyskTL1yJW6qDk1gw8yLCRwhZeQMoAF4YIwojpBCrhZwGJZaaPDMxNEA1a06UHFSyyITCWa3ihHobUQJqHClwV/GecCpZsrFIjq9TXcIy0Mni4saC2wEgIVYaWAjiShniiMASuYSeFWBKs8u/8Wco5zQ/u114atUttl2jFnCRn8W8sjlWCiJMdOMIkw4CYBXRnxqsNGYlkH5Ux5TeoOQ/MFwf7ksftYpinun2rgvYXjiBroRvFcOfK2pIJFwBhtHwMHA7oSYwKesL/JZmwzpOPXrYjkgrw+QCLGXvQTiMqkprAkGqwBsJE5jtb2P/YN3o0lvCE5Qs58Rtnht9zTT8NwVCFzcVSZwYWuq7C69NuxGhZSKcS6A4nm4agM9WowZ7lLUflOEFd4cNSPMwnylscGbkAnSsPQLMEG/KkwQOwJ2Z18dYGc/a9n3U/R9W2TZvz2OZU9d8MoQoZSCYOLEhDj2turzofCuCArvjgMFoDfCCsgPpreQWET7zPuBIdsUfhtKnXcpPO6LGcL3FdxMzgxLaNOdAWkCYl8h+DOKQmsuQAsopjnYxYLuKSemMnbv+yLc9v5YuE1LbTI6pOBMquD37NHmzQLiPgXEz0WA+PmogdiP2PscJIYs4PA+lHo/p+CYroYjzDKJyT2thdCjdn2jfCZYtlib6xcSCbZ2czTxxn5zEB4wnsD7YNE73reHWMQUU0exL/gmBc2gmEIaVBqbRgjKnJMI9jGXCpwQAjqIYFLfQpwswTdIwfmhiOD7sIvKmy3Q3KOnifZSbZIp9WLm+pBC47GQ3Hs8MBy5N3LlIQRfHFPczkT7WIRBPh6HZWAKEonpxKmooJjisCfb/my0jDDMx5BFpik8HgqEYR6qEoZJ6xmTVqUFuJsSK4SlNJs+OXhjp+HIlXGwDyEAjykAxgUAGFcFgDnPMxZGpmVt2aGwZdlpDyG1xylqfyoifj4dXvzMrXnwL4TSmnIkOMUI68i9UIxGGHBXxCDsT99GouRTirZfC2nbr+uIO9OBh3MyDqRrP66GJbBd+83JooyJyvu/ppA5/WPzYTj+S5G1b0/ZjAM2Lg6fTxMPw4aY5eOP2fbUXnTqMpqfLaP5WXGanx2a5iJH87t0T8CSKX6+jOLnxSl+fmiKh6kLK9s3pnsGIiuVyiH482UEf16c4M8PTXBbfcLzkZzvl+RLegpGRAq77sRvyGy9hl0GZ+TP7DU4f5Xm/FVa81dpx29MD8J8iGZ3IpyDdusE8G2XQ5kp4M19rentH2JlAwt0RH3xWvXAINWbkLgrvaZ6gdCuBwipFoWrG33VC4NOXTBYbFOI68UJhTyydNgtUvHF+gnMTqpQXIItusql+l1pyp5tQtmzKlJWHIay58soe74JZc+rSFkZm0Kleq7Pl1H2+SaUfV5FyvL9Unalv2Q7RJzNvSXzK3Dea7rGa/wme7Vm8mqt5NXac29n/tN6IFd5UNcV6enOii2CXfhQWxYCZj7Gnr2onO2VK2K25PKiqo9Cyo+a9aM5AhjadYEh5UkdU6v9Tn1QWPSlUL24YQMdfxpq47NQC5+t0+k0qctJeHbTavGW1d+t+IBN9DctMfa53+VVXHFXoIJwDZtk5Iwc01yWZhUcgb/nuTg1oH86bwrrI9LYrdrIopThVC8vIo/CPrOzJrKc8LUKm4Vnt6yqbgd/zDncJKmw6UYKm1VEYdMyp6e1asAfxz3Dqw4ApDQFOcatyhogkbVTVivvLp/OppUHIsN/qJfxtEm5xi/r9Or8jsQvG2JoysICFAnfAsWIrLuaSEIpIVxJgYlCovSS2nQngc/Fdoc+b+yObIPGLM8uElp7n6NsRkYhRTDjWAskBdln1W0+pH4tgtOvB+WZXQIBzjzSmFDEsOkjKsrv+vDZRgd/TWHiF22B5m/pzpdVoWCabSCNFCdYUKaojpqesaAJB5aIUSK0kOq4Km/9DNfxtyJ899tx6SqhEKZCM85U2V0Hfgl57rcUHj9W47FQD/Sj0uwG/icjwnRWYVhJIvWLBjtkG4JfdmHcnRZMPzuISbGvkXNaCao4g/8hLtF+m6Zk1IOeWl31IwXLbaEpibeHVlRZQYNsdjFxHOKSoF0+J4gyRMtvGrisZHQcwnGboVjOCiYTboyIsZm64UsrfNlBrht1lQDzWFGlFEbyUGWj8YI/y6DwdB2FF1vUHHrRr1EXxGVMIDPlRyDNqZRWXRyooDSW9EVTFqO5EtMMzF4Ur/6yp2wG3U6qv6IW+yQf8wQDm5TGmmApBKbMBoBUYvRQZHSXk0V6sRySi+KQXBwaElqoyjeYFgiSC4guAQKqKgDIy+WAvCwOyMtDAxJySE48wrE4WpmuZ0hHDTepi5higoBPgjkW5lfsdybOMmReLUfmVXFkXh0amYbp65i/XDicnEbBClMMS9OIM2IWjecHUInS8rSt+A9HFc1XpL6M39AENFlbw2T+Kt78VW7mr9Kdr2vtbVHXSuZg/7uqa/X2td7x1g9RYMBRA+6HsNDg5yHOmZl7ejyTc27qAVG+QUd2Qot0NQebS3CEJCNM66OBq1sPuJaOO4pnhiGtFEfSBPqFZHzVQI16IdSrC0KFRh4JVwtwYBBWSgmtcZ1mvBXyU9PBtBeblNbNTtomyLCH4cESVBlXyMzpZpHj5PKE61NmPePFMqJfbEL0iyoSPfA3BRNCU66A0urgRH+5jOgvNyH6yyoSPXAqlVCSgoBjKqS5AqeSUUYIFVJhHqmiwzmVaQBebQLAqyoCEHqOHEtlBqhxLe34GHZYz9GGkC/m3pL5RTzvPy5PLibJq3nJq90kr9ZNVvj2tqrwJQm0Dzwmt8z6Xm/5Mt/uIcr1JbGrEeHYTHuGVw66uEaWVC5XsuoIFXMluUsVMcP/mFCKYlonwzeXK1l1uNa5ksRVRpEoqrDSCoA7nthMry4IFXIlGXAUeCBBH2JsAK1zBnSmqRGZGKExcJE0Bl6sMy14ZFLYuqUbW7dkxWtUt+TFbzcxI3j5dUsZ67DUWPS2lRqlzQhfGjPTWhOuwWMEpmLwT434Zo3lUHlsciQmUSPwsKBYmRxaIuXxxDRnoqfaKK0POx+t8e3VBKKYjxpLGalBpAugKQG2nJAmJb1OnJTHQogicC+TYYMFS+FimYUgwrO71kLozhkGc3YCDe2Emw0rm0UlLIRS65q7leeebDUkNIgyGesh6RJNlElyovAFQ6xG3JPPZa06TAU9ouONMcxkUbUBy6OVjtm+qzxA+YJ2FEd2HnK1gMOw1EJjLOsbEkpu9VyWvsUznzoYjpwjeBWMO6oDBctcUoDOOLuCy9ioZwgjhBSjgpi51DvZPVpF8KuDEjxc4roIvU1sbwOKM5dxTc2OnRLARohZigtt3nGEJbwggvdO8dcHpHhI8P0XnAsTASUI5BMyceuI2CDhMNPgmhIK5hzmurzN0cvQo7gK/YnXyxwPGR7mz0KTLHQ5ehv6GLK8TUybWHXoMKSfZbxu+wC7tl6B4QliDJheSFP1FelaihDXiFONQOEyIeN4PsbEfIFMqoU6HnfDrO+KY9UIpmZSLc28eMwJI7brlTa9R5jJs5CUUxGVs3BXY6JBmHOEBKVsVfVkvcDqZdmw1QILGItwrCkSptiIIRoZNuB9GH5iGmxVKrCiIWNpF3QAZuAQcmZimLkYa4NK1xLCYD/5nYeMgvLXVu8sKpyrYilQV5WqlwUmYyRAVAGoEsm5Wc3gWnJp3BUi1W6MqVyE9q9Jisavi9H4dbVoTE2IGFGCTeGY0sqSmAmQeIQAkwHtFVGltY55bZPB0ubToGjrmMF2W/77rk0GpSPAQtCwmjU38arIGycurG0stCRYIKZiC9b0/WPc7PkTsCjA7F0hyLaZ8lyCIMvG3trPGbv6D0Wxf6h4YTpcD6w9xMEyBGFGMFgftk8TEZQTCQ470pphHqXnCEYYA3OSELAfV224bdOtoQTol7V9GFjGf8iA/00xIftmU8ZP1o3kR3/m/EZtHfKWURPighegscQAtSZBKm8ogZWUCj7lJkinQQ/aAXkI/AnwcKWUxn/IlMd4Q582T6uaz0Vw+LzZaPHqtXYSrgY5TIJItgGLVqIP4dqcpWQfwk23e6rXNIgbOMD0B+cZS0Y0OXirwYuCJTZH1MFJgybDiimBwMsSWskDtBskUa5ghur4UtRy+FJ9y8E2dwBLQTJMFZiKYEISW2OIwHwAox00BDNRpuNqOPglq4dEwVKfbc2DbWIcu1RLs/GJpTUZ/Bxy2qsMFB4L9o56PCQM+a10ZsqrJTHNbZWk+qDdBj/vwoS7LMYtl0ekq5TLwbNmDCswrzVmaq92XEa3wUvr5TxmMNCoUL/B0aH11JIhBRkMA5QVyKVgqVEiEeWMcL0qDHuQhoOjDER+KsYqP62HJNvj2UtsD3FXYMIYA2ITJA7WcDBe8z9lUPhrQaXx9dCrfr3GQKZSXVGQMKYRMEXc7iUdpONgLO2LlldH0bivGaBdFu/ZZU/ZDLuNe3atjn1jISgGZlCUYMpxJME40kqDm8+NdU33Uly9jOZXy2l+VZzmV9WjOXNNCwfEzOapolrHbQO5Bg+GaWUcGdOts0Siv15O9NfFif66ekQXLtXEhBMZOIRxoBm5pnRQAxKCgftuEpxLS5SZ7xx3Fb8hCYJnps7Mn3g3f6I/33Ludosuc3IOv4N3mdu+wjT/zv/dvhburstkC6XVCJebZDAqCHzLMK5vDmsqBaoeeBVNrSEuqAEKPw8gBjWsjic9/LYegBVMr6Gu5mDjYmQyMRHolzpxWCFLOMtlv9yk1dDl8oYE5aVFR9k0eVvYgrEsiUIKg13MQZLGQ4USxrIs31bOQuVqE1SuDobKGoNZUgpiEPgRK65twQZPGsy6fHs5i/CvNyH860oS3hjNJtEGGwoTTOy2FksazSVmlyebZV0lq14TlF9hOtvT75Kn+8mi2dutmmvJBKAHz0svtfj1bvli3vY59mtH65VmtAKrjHEMdhmW2JSU10jJ5zKjqw9Y2pCWqwxp7QohsNbg+igzO+Po7OjqI1bMkgZ4jTfLkVQAF6W0ThUgxcujrpIa53Kd/lK2aoqG59/aRg12OUQNnfz47SaqSx0g7pNZS1WmzvI3rlv+v2qq8qXfxnl8JZZTrd8PZhK+ERycR8lMLfrxqacawJRtAzaWMNXx24DVh2zWYWMpZzUYcQFLypg0yYEAWX0jctmGxJWtEFrwfANz4GqdIaFPovmSkSFxZw2Ju6QhYfl4s5psXRFDolTn97YGhsT/lfrGoYoayLsclgSnpmKKSqKVwtiE644HodropSWxicYSrmocf3Si+pIwly1RYzM9X/Znx0bE2xkmw9tiOxlvN97D2LTwcNUOhna1KY4C0QiaCwz6iCWJyzQx5d5SC4WZmLVFZhQTQWgwcIRlp4VuVlq4dGPVFu48pij/rhjl3+2m4nNHCVc4bkGNourd7O2hzai5pHja0vJdxjoeFy2CGh9+Ja+zDMJ82tAysBFvkqvWqV6F0V9CWFspUM+Lsch51TpPICuP+Eom2WwP9XTQ7S+Km3Mr6i9t660sXvmf/7+aqs3gypZkcLQ5H37S1DK1yyUC2UqJkJopU9Kd9uu2FE00J9lXhWjWJJo3R+05QWWLcPr94dcP3k3f+xYQOO/azqwLeG0l1psUBj8KVgX8qH5VwCHLxl7b3ZA5I/bbwwjuZeqpIgJ98r5NFic7B2f/8ct0OPnL6fXH6/Z173pw7V9P4B/iPHPCb5x/cpLnwQfRN+37//5b+OeJ8yQF4gTueLLi9jvgml1DukjZxIjsxRQrYRsWp2TVSurjBN1fXr+/HgHNx9f3181rnCY63pbc283F2UXaTSapm63xsD+deB/bI88bvBm2w+q/sGtG2CaDhS3t86/rFZTNXM9br+RdjxzaM2FZ1LKUUVWIsHIFYWkGYeW2hJVrCJtdZrdv33oFZQXSEWV1McrmEMWZFN6NKJb1EcWXK0RxlOwaugf5BXEO2uMM2uPd0B7Xh/bPV6nBeFuRbRYleGvN9mmGtf68mBP0vOzOUGsDNFKZmLWSNKrPRa7W0qRTY9M4nyvNDxefeWMpn1Ub974Y5d9XiPKm65YEajKMtOnBhmxFnOQMBLTUykTG4i2gPTbdejea9Ibd4aDZz2gW8N6SP93DoVeoVUDv0O7RXNhGmICyNLk5GJsBbCoRw1HKJRqWvQALBJHVw9m26F2zISDPlwNyXwiQ+woBIkEKAcXNJHutkNBJQKQ2g0ExYRLYRfOV9XN7AWRZWOx+ORY/F5NMP1dIMlEctCsGJMyMQoAj2qGhAIMShAMOTCPKogJpakaxaYQwyCwzTEXvUDQtI3xvOeE/FCP8hyoRnlPXNMElXHKCVNyIkcI1FeWCaM65woRG43KZi4RQHFHBgkzeHRI+O74fK4MPGbp4UjS+Pzk46ddEzEx0H6wgWNJCgkLQOBnrB1PelYhJIRCwDBOryw4rHvnPBjxWNj9nAN5cl9+8CHhz6ySCMhBH8//TScSxdE1bXCmB8YAVhapxE9wl/cUvl7W+/lhMsH6sVB8i5kqJtTC9jDHmctZ0CxFAnHJONQXlhvfRgiubtaIEwo8ZjNUpylidTSeRlNdkXBAF3MRMxzMeVCwGbGWcSYY1F+ABMcaUHfmFMQHDHMGnSMDfeZismk3G12YdTFPofyrGZ58qmXXA9pJ1sIyaP1s19SNFzV+KUfOXg9skSTtcYKQ1yCZO41FegroKAzNRDca56cW/dyt8bWgmqwz712KE/7VChDehGcVMEppmyLTcFrbZLUbSTPUChYFQ0PJ5z6GZbNXxIaT6+wyq94uqjv62Q6xKUB6wquetcMFZlC5N3KA5PaKEEKY4ZnH3YVD0BDFOmcQrh+1UTn1kbwYkt2M/tnsDfzLp/f6fPc/pXY+jsP6T9VH9Q/PYukC+BRxwVsQ0TFIUC4qwTREVgpmyO8WoJpyJxEiYbVvSnhfrZX++3pnZ52QBmwyzm460JthMJWFaEPBr4pGRe+lIu2zmTmQQnWfMN7ovKtXuqy7VbDIOFqA9JDPtiygzOeqh1QQrnTIzNZWA6jcjOeokwgoEs88t6vcZqA/WoZ4IZw+2HCW+y3B2BqpzUQSKaVCUT4QkZgiyWJXQXmo8ux+CMcgA46yYdDzbVDruxfsnnLoSGWdSI46FbVpBien5CTKPEal0tMkpwHogWivwQKlmev+tiWMeOMsg+3Qd2ReSEKd1EXwHykI8T2ch5oDobJVyeiwI0WNdIGocCKOzdRhlWxCfrDeaxUcPRS2Ih7qgZJTJovUWbE4IV5uKesY02MoUPNc62RDZblAyd7KX3++pJJYLfg/WLsbYpH6Az4oxta3ACeVcgHYCUwIsB0xpPqdn+Z51JMtuMjOZCmn555XS8oy7nFPOzM60RCRqeW/2bDBVoOQxRsAGKHIawSLACLQ+UYqwYJN7d3o+q/DjuaX7z7bf3fOswo+/rab/QuHH30oq/Ej0p8pbzX+4wo9s6UET0uPzsD+Fwx+9EVzKb/ecRzj6/cgfw4fOvT9xpgEDtXu+1wFZ14NnfTmaDjo3/d//Hd4NjPzKL4A2HGi9z/2ZmyH83LE38m9inh0DzY1PemLlPM6UVCZCwyThmhIKtjPRWKvQxQlYTSJgQbCgKSV6mazKRoglEHo7ncAS6Pie0/K+et0AhIHzIryG9//++I8Y/eX5dATQ/eZ75qvmwOl4984Q1EvXG8AH76eDu4lz1xwMxhOnM3WaUzi40xw7nZHnjz1/4nc9p+uNmkCvAPqm4w8cD/6dO2DsBIvgBv6Ijvn9v1re6Ob3/+qNvIGbfw1sOIF+n2tgAVgTaiVSUDPNTSsuTbV1gCtIVmwGg2IpMOcongSaxnWFtnixqbaYp8DBo2XIbBlLySQTFGsEWkdzW0RIgThKMQxfYgI0LGee04tlxZlfCgVQvlQogIJc2xAFRUOCNKMCC2WafIOpW3rEJIvsVqGnCT8qRPhRhQkPa5poJrlUIAzAsCid8Fmx+1GGg/dbse3G3zbNTqlc9J66ZjyzFoyb3ufETnoySBJwJSTnGiuCgX9KkkaWLZopjMaF2GJcHbawvradcclcUxohhQLeUAT05J7GmxYi/G82/pEm/KQQ4SfVJTw2AVvOOcaKmvR8VTrhs+TRJEMenRbzpE+PZjeRINcEowilEgcjzeRh5dHpcjXdXNdXL8EWzY3bKe1fTWMEBpICs50wphhRMlfOQxlbSuNYHVzTFAAXxZjkolLhJukSwQXCQpiEICxkiV5Adk/KWPVe2N4ip7av5G/Le1Ga7GRzkmebUd5c8/Ck5jUL21D+2LCTNVx601VYPGCFQpCD11b0OutlvbWznL/7mpclKLZ/hD1tH8AyptLMF8HULNpogjvVrsZcYgIyGyO+L3lygN54ZnVXHh3TWEpxhZHiZtIR0pFVD8a+xIJgiU2XSawRt2hhk5PIJFGCU4mOBy4jgyoPV7xjuoSbGoAPJcRsQyjEiFD0aPD5sfE+aYn4LOGmxiI7YTtohhKEkCBaw9FiZbvdqqGVy06IrIRQ3V8ke1e/WNe7GmNrLzBrL4jw1Jvo1Mhq8LZqXo1XTG7ate2wvNdNuXbDVjsEZTTYjWwGF9iDM/DCiVZIIzZr32kqhjkzTMX2Vjh/EKNBVBuaWY9q5nLQMEhh8D6UJFK/aDBbIQJyTlCsFDUVInJPsdxDwBMLnkqDNDMTljIQMnmhSCKTvoB5rurSWiDkLe9IXSWEZu2ol7JRg0gXMDOzR4SQlClaJz7KYx5chPr9ZajdXybNg4u15kGcXiTDC3SDuAKc2o3XQGAeWKblm5kHpArmQamTLQxFK809ZqwFRVyZpHaGtaZ2UKw0XCSIzcEScczSFP9iqcFdwvmaJ1SEjVYD1a26mMu2FoQGlSNjcwFcWU2U2VWk8AU7ophCtx7KKJubGgvsRHSY0NjgLlUmR4cwARYepkdkfceaotJ45TEeam2E58nCfxVq/1dLzYR+0TZB/U0rw6vke1GXahN/UlhIQZnIJUyr2TcmG/e4BUNWVnNrXQxoEfPWxlsoZU5+WNEp6JgaBWV7CadRsU1o5J8lvYTTtV4CtbvCPLxAK4gawqmtZBCxuV0QkZbuJWT2Ii8zjNjcUk/urZn68rQeuk19WcWMldaWUagSyJ8YaBeKK+3uKZPqEAjsJBpYIhs0ZnxwPCg0d+JklYBCihkauF7yKI+2Povql0Nle57U1mdrtTWLUuistm7bmF47GdNrbRfTY9XQ1qVG9VrVV9epdEN2RHKqXX0JldbXhLjyiCCoi6qwfNDAsapw8437qwUOrZ3E2Q6jsutlwObqvRzFU5Yq50mxmMqk6qhmuCUiJ3tVM3CywZDUTtFIWacWkbJjmpG6JBxm5zQFQbH4zczYDu3lxJCiDEObR2GxuSAYmQlmkTS6oxBZJ57QvpHRzZcb3Wumae9wzZUaINsuPlB2gx8bHAis8OVcU7XJ5/lMjQ3T6kpsPrtYD73S7q4XCO16MUJjVgV6PBjMhHfFMUh7PrXihFx58fM6/GJeh7+c1+Gv1uhwEeXHJ3X4TVKHd5M6vLedDhd/bzrcq5foWpLwC+oFIyw0Y/AtZ5hrtioLrmo8lS9rp/oqPkfSos2ykq7myrSgR0gyEs/cOgK4uvXiqOU59EgrxZHEhBEhGV+VYFUvhHp1MRUKpS0KV5u2YggrpYSZ8lgjvPIYFZfzRsXVvFHxeo0dIcNz7ua22OAsf+4t2BG3MdtuZDjIvzfDYUbNijMR44ggxrDp4WtmXkRaiYLQ04hTM2hGMCEtE8GH0gzMgG+BvY7HivDrgZexIiSgYmZpE8xB99i4gSbcTADgBEnK43HOxOVMU/h1ALHSWh2Plrqtix1hRjBoigRSTDJEZdzz3PAVWHYYU4EVjfK2XTPMgYPeQhj02upRn1UDLJeaihRUqGSukgkil2sTRFR4um+93VubzmmXAw/9XH87daVK7CcTLcTMqvAyE0T8bVmpjEqVQtqKuRSb4euII83MNKcVvFS1nds1wq/6WCV2WTEzjpIET0oRJakOqxWYhG8E10qbQd8A6vHgs12GQ4koLbKUtl5UJkspMCfAFQaDAktsSpOPBjF/N+ZEmdVfS/mqwYgLUFLGJHjC8MLrVPOax4qIhhq/Tji41oq4WmtF6PD0W5tmeme93LtktPw2Di1uZEXoalgRbOv1V0Qx1UHkFXKhuGvG40mwyhESwFR16tK0JkaxrbdbCSuCwyGAiyRaKdNei9RJ2OULIlVeKaVYSlozIpOnGtoVQmAzUVcozsXKsES9ILvdzW5UReyIGhvo6yclvbelxB/spKTTrElJ/7Fa+S9MSvqPQ0xKyrkwyhmUFP/8eTSAfIMxPGWArHnf9YZdrzVq/vV/AVBLBwhJAKol1ygAAN2vAQBQSwECFAAUAAgICADOrF5BRczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAgIAM6sXkFJAKol1ygAAN2vAQAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAbykAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /> | | <br> |
| | [https://ggbm.at/r6yKgffu GeoGebra Applet "Volumenvergleich von Prismen mit unterschiedlicher Grundflächenform"] |
| | |
| <br><br> | | <br><br> |
| {{Lösung versteckt|1=Es kommt nicht auf die Form der Grundfläche, sondern auf den Grundflächen'''inhalt''' an!<br> | | {{Lösung versteckt|1=Es kommt nicht auf die Form der Grundfläche, sondern auf den Grundflächen'''inhalt''' an!<br> |
Version vom 17. Oktober 2016, 12:54 Uhr
Vorlage:Lernpfad Inhalt und Drumherum
Zur Person

|
Bonaventura Francesco Cavalieri (1598-1647) war ein italienischer Mathematiker und Astronom.
Im "Satz von Cavalieri" (auch "Prinzip von Cavalieri" genannt) geht es um die Volumengleichheit zweier Körper.
|
Erarbeitung des Satzes von Cavalieri
|
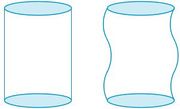
|
Peter: "Gib mir das rechte Glas, da passt mehr rein! Ich hab so einen Durst!"
Sandra: "So ein Quatsch! In die Gläser passt doch gleich viel!"
|
- Vorlage:Arbeiten
Achtung
Zusätzliches Anschauungsmaterial zum Anfassen:
Wenn es dir schwer fällt, dir das Ganze richtig vorzustellen, nimm dir vorne am Pult zwei der Bierdeckelstapel und stelle die einzelnen Situationen damit nach.
GeoGebra Applet "Volumenvergleich von Zylindern (1) + (2)"
GeoGebra Applet "Volumenvergleich von Zylindern (3)"
Zurück zur Ausgangsfrage:
Wer hat nun Recht? Peter oder Sandra? Begründe deine Antwort!
- Vorlage:Arbeiten
Du hast gerade Sachverhalte herausgearbeitet, welche Bonaventura Cavalieri in seinem berühmten (grundlegenden) Satz formuliert hat. Du kannst den Satz in deinem Schulbuch (Lambacher Schweizer, Ausgabe 2010) auf S. 22 oder Fokus Mathematik, Ausgabe 2016 auf S. 44 nachlesen und deine Aufzeichnungen - wenn nötig - ergänzen oder berichtigen!
- Vorlage:Arbeiten
GeoGebra Applet "Volumenvergleich von Prismen mit unterschiedlicher Grundflächenform"
Es kommt nicht auf die Form der Grundfläche, sondern auf den Grundflächeninhalt an!
Bsp.: Ein Prisma mit quadratischer Grundflächen und ein Prisma mit dreieckiger Grundfläche haben das gleiche Volumen, wenn ihre
Grundflächeninhalte, ihre
Höhe und die zur Grundfläche parallelen
Schnittflächen in gleicher Höhe gleich groß sind.
Übungsaufgaben
- Vorlage:Arbeiten
Das schiefe Prisma besitzt das gleiche Volumen wie ein senkrechtes Prisma mit den angegebenen Maßen. Also: 
Der geschwungene Zylinder besitzt das gleiche Volumen wie ein senkrechter Zylinder mit den angegebenen Maßen. Also: 
Zu deiner Lösung gehört auch der Rechenweg!
- Vorlage:Arbeiten





