Jahrgangsstufentest/BMT8 2007: Unterschied zwischen den Versionen
Main>Andrea schellmann (layout, typo) |
Main>Andrea schellmann (Lösungen ergänzt) |
||
| Zeile 22: | Zeile 22: | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
:Die Statue hat dann eine Gesamthöhe von '''16m'''. | |||
:Möglicher Lösungsweg: | |||
::Man misst die Höhe des Fotos (z.B. 5cm) und der Statue auf dem Foto ohne Sockel (z.B. 4cm). | |||
::Die Höhe der Statue auf dem Foto entspricht also <math>\frac{4}{5}</math> der Höhe des Fotos. | |||
::Damit entspricht auch die Höhe der Statue auf dem Banner <math>\frac{4}{5}</math> der Höhe des Banners: | |||
::<math>h_{Statue} = \frac{4}{5}\cdot h_{Banner} = \frac{4}{5}\cdot 20m = 16m</math> | |||
}} | }} | ||
</div> | </div> | ||
| Zeile 32: | Zeile 36: | ||
<div style="padding:10px;background:#ffffff;border:1px groove;"> | <div style="padding:10px;background:#ffffff;border:1px groove;"> | ||
<big>'''Aufgabe 2a'''</big> | <big>'''Aufgabe 2a'''</big> | ||
Die Tabelle zeigt für einen bayerischen Landkreis die prozentuale Verteilung der Schülerinnen und Schüler in der Jahrgangsstufe 8 auf die einzelnen Schularten im Schuljahr 2005/06. | |||
Diese Verteilung soll in nebenstehendem Kreisdiagramm veranschaulicht werden; die Sektoren für die Hauptschule und die Realschule sind bereits eingetragen. | Diese Verteilung soll in nebenstehendem Kreisdiagramm veranschaulicht werden; die Sektoren für die Hauptschule und die Realschule sind bereits eingetragen. | ||
Ergänze im Diagramm die beiden fehlenden Sektoren und beschrifte sie. | Ergänze im Diagramm die beiden fehlenden Sektoren und beschrifte sie. | ||
| | |||
''Hinweis für die Online-Version: Du kannst dein Vorgehen auch beschreiben.'' | |||
{| | |||
|width="100px"| | |||
|[[Bild:2007 8A Aufgabe2.jpg]] | |[[Bild:2007 8A Aufgabe2.jpg]] | ||
|width="100px"| | |||
[[Datei:BMT8_07_A02a_01.jpg| | |[[Datei:BMT8_07_A02a_01.jpg|180px]] | ||
|} | |} | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
: | :[[Datei:BMT8_07_A02a_02.jpg]] | ||
[[Datei:BMT8_07_A02a_02.jpg]] | :Erläuterung: | ||
: | ::Die "sonstige Schularten" machen 10% aus. Dies entspricht im Kreisdiagramm einem Kreissektor mit dem Mittelpunktswinkel 36°. | ||
:: | |||
}} | }} | ||
</div> | </div> | ||
| Zeile 104: | Zeile 111: | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
: | :Zeichne zwei Kreise mit den Mittelpunkten A und B und dem selben Radius. Die Gerade durch die beiden Schnittpunkte der Kreise ist die gesuchte Mittelsenkrechte. Der Schnittpunkt der Mittelsenkrechten mit der Strecke [AB] ist der Mittelpunkt des Kreises, der [AB] als Durchmesser hat. | ||
[[Datei:BMT8_07_A42a_02.jpg]] [[Datei:BMT8_07_A42a_03.jpg]] [[Datei:BMT8_07_A42a_04.jpg]] | [[Datei:BMT8_07_A42a_02.jpg]] [[Datei:BMT8_07_A42a_03.jpg]] [[Datei:BMT8_07_A42a_04.jpg]] | ||
}} | }} | ||
</div> | </div> | ||
| Zeile 126: | Zeile 130: | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
:Dreieck ABC ist rechtwinklig bei C, weil C auf dem Thaleskreis über [AB] liegt. | :Dreieck ABC ist rechtwinklig bei C, weil C auf dem '''Thaleskreis''' über [AB] liegt. | ||
}} | }} | ||
| Zeile 143: | Zeile 147: | ||
Kreuze an, welche der folgenden Argumentationen richtig sind. | Kreuze an, welche der folgenden Argumentationen richtig sind. | ||
Die zwei Teildreiecke sind kongruent, ... | ''Die zwei Teildreiecke sind kongruent, ...'' | ||
(!...weil die Mittelsenkrechte Symmetrieachse des gleichschenklig-rechtwinkligen Dreiecks ist.) (...weil man zeigen kann, dass die Teildreiecke in allen drei Winkeln übereinstimmen und Dreiecke, die in allen drei Winkeln übereinstimmen, immer kongruent sind.) | (!''...weil die Mittelsenkrechte Symmetrieachse des gleichschenklig-rechtwinkligen Dreiecks ist.'') (''...weil man zeigen kann, dass die Teildreiecke in allen drei Winkeln übereinstimmen und Dreiecke, die in allen drei Winkeln übereinstimmen, immer kongruent sind.'') | ||
(!...weil man zeigen kann, dass die Teildreiecke in allen drei Seiten übereinstimmen und Dreiecke, die in allen drei Seiten übereinstimmen, immer kongruent sind.) | (!''...weil man zeigen kann, dass die Teildreiecke in allen drei Seiten übereinstimmen und Dreiecke, die in allen drei Seiten übereinstimmen, immer kongruent sind.'') | ||
(!...weil man zeigen kann, dass die Flächeninhalte der Teildreiecke gleich groß sind und Dreiecke, die den gleichen Flächeninhalt besitzen, immer kongruent sind.) | (!''...weil man zeigen kann, dass die Flächeninhalte der Teildreiecke gleich groß sind und Dreiecke, die den gleichen Flächeninhalt besitzen, immer kongruent sind.'') | ||
</div> | </div> | ||
| Zeile 159: | Zeile 163: | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
:'''<math> \frac{8}{15}</math>''' | :Der Wert des Terms beträgt '''<math>\textstyle\frac{8}{15}</math>'''. | ||
:möglicher Rechenweg: | :möglicher Rechenweg: | ||
:: | :<math> \left(\frac{3}{4} \cdot \frac{4}{5} - \frac{1}{3}\right) : 0,5 = \left(\frac{3}{5} - \frac{1}{3}\right) : 0,5 = \left(\frac{9}{15} - \frac{5}{15}\right) : 0,5 = \frac{4}{15} : 0,5 = \frac{4}{15} : \frac{1}{2} = \frac{4}{15} \cdot 2 = \frac{8}{15}</math> | ||
}} | }} | ||
</div> | </div> | ||
| Zeile 176: | Zeile 180: | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
: | :0,5 muss durch '''0,25''' ersetzt werden. | ||
:Begründung: | |||
::Wird bei einem Quotienten der Divisor halbiert, so verdoppelt sich der Wert des Quotienten. | |||
}} | }} | ||
</div> | </div> | ||
| Zeile 197: | Zeile 202: | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
:''' | :Die Fahrzeit verkürzte sich um '''60 %'''. | ||
:möglicher Rechenweg: | :möglicher Rechenweg: | ||
:: | ::Die Fahrzeit verkürzte sich um 42 Minuten. | ||
::<math>\frac{42}{70} = \frac{6}{10} = 60%</math> | |||
}} | }} | ||
</div> | </div> | ||
| Zeile 222: | Zeile 228: | ||
Multipliziere aus und vereinfache: | Multipliziere aus und vereinfache: | ||
:<math>\left(a - b\right) \cdot \left(a - 2b\right) + 1,5 ab</math> | :<math>\left(a - b\right) \cdot \left(a - 2b\right) + 1,5 ab</math> | ||
| Zeile 227: | Zeile 234: | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
:''' | :'''a <sup>2</sup> - 1,5 ab + 2 b<sup>2</sup>''' | ||
a <sup>2</sup> - 1,5 ab + 2 b<sup>2</sup> | |||
:möglicher | :möglicher Lösungsweg: | ||
:: | ::<math>\left(a - b\right) \cdot \left(a - 2b\right) + 1,5 ab = a^2 - 2 ab - ab + 2 b^2 + 1,5 ab = a^2 - 1,5 ab + 2 b^2</math> | ||
}} | }} | ||
</div> | </div> | ||
| Zeile 240: | Zeile 248: | ||
Vereinfache so weit wie möglich: | Vereinfache so weit wie möglich: | ||
:<math>\left( -x \right) ^2 \cdot x + x^3</math> | :<math>\left( -x \right) ^2 \cdot x + x^3</math> | ||
| Zeile 245: | Zeile 254: | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
:''' | :'''2x<sup>3</sup>''' | ||
2x<sup>3</sup> | |||
:möglicher | :möglicher Lösungsweg: | ||
:: | ::<math>\left( -x \right) ^2 \cdot x + x^3 = x^2 \cdot x + x^3 = x^3 + x^3 = 2x^3</math> | ||
}} | }} | ||
</div> | </div> | ||
| Zeile 264: | Zeile 273: | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
:'''''' | :Der Flächeninhalt des Viereck beträgt '''12 FE''' bzw. '''12 cm<sup>2</sup>'''. | ||
:möglicher | :möglicher Lösungsweg: | ||
::[[Datei:BMT8_07_A08_02.jpg]] | ::[[Datei:BMT8_07_A08_02.jpg]] | ||
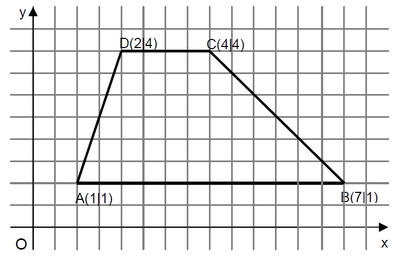
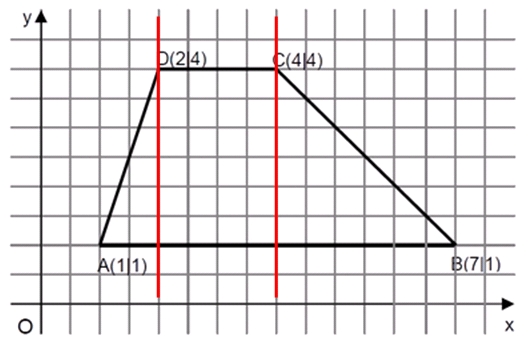
::Zerlege das Viereck (Trapez) in zwei rechtwinklige Dreiecke und ein Rechteck. Ihr Flächeninhalt lässt sich leicht aus der Grafik entnehmen bzw. über leicht abzulesende Seitenlängen berechnen. | |||
::Berechnung des Flächeninhalts: | |||
::A<sub>Trapez</sub> = A<sub>D 1</sub> + A<sub>R</sub> + A<sub>D 2</sub> = 1,5 + 6 + 4,5 = 12 | |||
}} | }} | ||
</div> | </div> | ||
| Zeile 287: | Zeile 300: | ||
<div style="padding:1px;background:#ddeeff;border:1px groove;"> | <div style="padding:1px;background:#ddeeff;border:1px groove;"> | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
:''' | :mögliche Lösungen sind z.B. '''1 = 4cm und b = 1,25 cm''' oder '''1 = 3cm und b = 5/3 cm''' | ||
1 = 4cm und b = 1,25 cm | |||
:Erläuterung: | |||
::Das Rechteck hat einen Flächeninhalt von 10 cm<sup>2</sup>. Da die Flächeninhalte des rechteckigen Lochs und der Restfläche gleich groß sein sollen, beträgt der Flächeninhalt des Lochs 5 cm<sup>2</sup>. Für die Länge und die Breite des Lochs wählt man daher Werte, deren Produkt 5 cm<sup>2</sup> ergibt, mit der Einschränkung, dass die Länge kleiner als 5 cm und die Breite kleiner als 2 cm ist (da rundum ein Randstreifen übrig bleiben soll). | |||
}} | }} | ||
</div> | </div> | ||
</div> | </div> | ||
Version vom 13. September 2009, 09:35 Uhr
Aufgabe 1
- Die Statue hat dann eine Gesamthöhe von 16m.
- Möglicher Lösungsweg:
- Man misst die Höhe des Fotos (z.B. 5cm) und der Statue auf dem Foto ohne Sockel (z.B. 4cm).
- Die Höhe der Statue auf dem Foto entspricht also der Höhe des Fotos.
- Damit entspricht auch die Höhe der Statue auf dem Banner der Höhe des Banners:
Aufgabe 2a
Die Tabelle zeigt für einen bayerischen Landkreis die prozentuale Verteilung der Schülerinnen und Schüler in der Jahrgangsstufe 8 auf die einzelnen Schularten im Schuljahr 2005/06.
Diese Verteilung soll in nebenstehendem Kreisdiagramm veranschaulicht werden; die Sektoren für die Hauptschule und die Realschule sind bereits eingetragen.
Ergänze im Diagramm die beiden fehlenden Sektoren und beschrifte sie.
Hinweis für die Online-Version: Du kannst dein Vorgehen auch beschreiben.

|

|
- Datei:BMT8 07 A02a 02.jpg
- Erläuterung:
- Die "sonstige Schularten" machen 10% aus. Dies entspricht im Kreisdiagramm einem Kreissektor mit dem Mittelpunktswinkel 36°.
Aufgabe 2b Die vier Sektoren des vollständigen Kreisdiagramms sollen mit den vier Farben Blau, Grün, Orange und Rot gefüllt werden, jeder in einer anderen Farbe. Wie viele unterschiedliche Farbgebungen sind möglich? (!4 · 4 · 4 · 4 = 256) (4 · 3 · 2 · 1 = 24) (!4 + 3 + 2 +1 = 10) (!4 · 4 = 16) |
Aufgabe 3
Wandle jeweils in die in Klammern angegebene Einheit um.
- 4,35 km (m)
- 450 g (kg)
- 3500 cm2 (dm2)
- eine Viertelstunde (s)
- 4,35 km = 4350 m
- 450 g = 0,45 kg
- 3500 cm2 = 35dm2
- eine Viertelstunde = 900s
Aufgabe 4a
Konstruiere die Mittelsenkrechte der Strecke [AB] und zeichne den Kreis, der [AB] als Durchmesser hat.
- Zeichne zwei Kreise mit den Mittelpunkten A und B und dem selben Radius. Die Gerade durch die beiden Schnittpunkte der Kreise ist die gesuchte Mittelsenkrechte. Der Schnittpunkt der Mittelsenkrechten mit der Strecke [AB] ist der Mittelpunkt des Kreises, der [AB] als Durchmesser hat.
Aufgabe 4b
C ist derjenige Schnittpunkt von Mittelsenkrechte und Kreis, der oberhalb der Strecke [AB] liegt. Das Dreieck ABC ist dann gleichschenklig, weil C auf der Mittelsenkrechten von [AB] liegt, und deshalb von A und B gleich weit entfernt ist. Begründe, dass das Dreieck ABC auch rechtwinklig ist.
- Dreieck ABC ist rechtwinklig bei C, weil C auf dem Thaleskreis über [AB] liegt.
Aufgabe 4c Es gilt:
Kreuze an, welche der folgenden Argumentationen richtig sind. Die zwei Teildreiecke sind kongruent, ... (!...weil die Mittelsenkrechte Symmetrieachse des gleichschenklig-rechtwinkligen Dreiecks ist.) (...weil man zeigen kann, dass die Teildreiecke in allen drei Winkeln übereinstimmen und Dreiecke, die in allen drei Winkeln übereinstimmen, immer kongruent sind.) (!...weil man zeigen kann, dass die Teildreiecke in allen drei Seiten übereinstimmen und Dreiecke, die in allen drei Seiten übereinstimmen, immer kongruent sind.) (!...weil man zeigen kann, dass die Flächeninhalte der Teildreiecke gleich groß sind und Dreiecke, die den gleichen Flächeninhalt besitzen, immer kongruent sind.) |
Aufgabe 5a
Berechne den Wert des Terms
- Der Wert des Terms beträgt .
- möglicher Rechenweg:
Aufgabe 5b
Durch welche Zahl muss man die Zahl 0,5 im obigen Term ersetzen, damit man den doppelten Termwert erhält?
- 0,5 muss durch 0,25 ersetzt werden.
- Begründung:
- Wird bei einem Quotienten der Divisor halbiert, so verdoppelt sich der Wert des Quotienten.
Aufgabe 6a
Im Jahr 2006 hat die Deutsche Bahn zwischen Nürnberg und Ingolstadt eine 89 km lange ICE – Hochgeschwindigkeitsstrecke in Betrieb genommen. Frau Dorn, die regelmäßig mit dem Zug von Nürnberg nach Ingolstadt fährt, stellt fest: „Für mich verkürzte sich die Fahrzeit von 70 Minuten auf 28 Minuten.“
Um wie viel Prozent verkürzte sich die Fahrzeit von Frau Dorn?
- Die Fahrzeit verkürzte sich um 60 %.
- möglicher Rechenweg:
- Die Fahrzeit verkürzte sich um 42 Minuten.
- Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \frac{42}{70} = \frac{6}{10} = 60%}
Aufgabe 6b Welcher Term beschreibt die Durchschnittsgeschwindigkeit in km/h, die der ICE auf der Hochgeschwindigkeitsstrecke besitzt? (!) (!) () (!) |
Aufgabe 7a
Multipliziere aus und vereinfache:
- a 2 - 1,5 ab + 2 b2
- möglicher Lösungsweg:
Aufgabe 7b
Vereinfache so weit wie möglich:
- 2x3
- möglicher Lösungsweg:
Aufgabe 8
Berechne den Flächeninhalt des abgebildeten Vierecks ABCD.
- Der Flächeninhalt des Viereck beträgt 12 FE bzw. 12 cm2.
Aufgabe 9
In Rechtecke der Länge 5 cm und der Breite 2 cm wird jeweils ein rechteckiges Loch so geschnitten, dass rundum ein Randstreifen bleibt.
Mögliche Figuren sind z. B.: ![]() oder
oder ![]()
Nicht erlaubt sind z. B.: ![]() oder
oder ![]()
Gib zwei Möglichkeiten an, wie lang und breit solch ein Loch sein kann, wenn der Flächeninhalt des Lochs genauso groß sein soll wie der Flächeninhalt der Restfläche.
- mögliche Lösungen sind z.B. 1 = 4cm und b = 1,25 cm oder 1 = 3cm und b = 5/3 cm
- Erläuterung:
- Das Rechteck hat einen Flächeninhalt von 10 cm2. Da die Flächeninhalte des rechteckigen Lochs und der Restfläche gleich groß sein sollen, beträgt der Flächeninhalt des Lochs 5 cm2. Für die Länge und die Breite des Lochs wählt man daher Werte, deren Produkt 5 cm2 ergibt, mit der Einschränkung, dass die Länge kleiner als 5 cm und die Breite kleiner als 2 cm ist (da rundum ein Randstreifen übrig bleiben soll).