Flächeninhalt des Rechtecks: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
{{Box|Lernpfad| | {{Box|Lernpfad| | ||
===Zielsetzung:=== | ===Zielsetzung:=== | ||
Schüler entdecken Schritt für Schritt die Formel des Flächeninhalts und lernen damit zu rechnen. | *Schüler entdecken Schritt für Schritt die Formel des Flächeninhalts und lernen damit zu rechnen. | ||
===Altersstufe:=== | ===Altersstufe:=== | ||
5. Jahrgangsstufe am Gymnasium | *5. Jahrgangsstufe am Gymnasium | ||
===Zeitbedarf:=== | ===Zeitbedarf:=== | ||
ca. 70 Minuten | *ca. 70 Minuten | ||
===Materialen: | ===Materialen:=== | ||
Computer (mit Java und GeoGebra) und Heft. | *Computer (mit Java und GeoGebra) und Heft. | ||
|Lernpfad}} | |Lernpfad}} | ||
__NOTOC__ | __NOTOC__ | ||
==Arbeitsaufträge== | ==Arbeitsaufträge== | ||
{{Box|1=1. Arbeitsauftrag - Quiz über Rechtecke|2= | {{Box|1=1. Arbeitsauftrag - Quiz über Rechtecke|2= | ||
<div class="grid"> | |||
<div class="width-3-4"> | |||
Nun wollen wir zu Beginn erst einmal testen, was ihr denn noch über Vierecke wisst. | |||
Dazu könnt ihr jetzt ein Quiz machen: | |||
* [http://www.bartberger.de/Mathematik/Klasse5/Tests/vierecke/index.html Quiz zum Viereck] | |||
* [http://www.bartberger.de/Mathematik/Klasse5/Tests/vierecke/index.html Quiz zum Viereck]</div> | |||
<div class="width-1-4">[[Bild:UhrPic.jpg|250px|center]] | |||
'''Für diese Aufgabe habt ihr 5 Minuten Zeit!'''</div> | |||
</div> | |||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
| Zeile 25: | Zeile 32: | ||
{{Box|1=2. Arbeitsauftrag - Kästchen zählen|2= | {{Box|1=2. Arbeitsauftrag - Kästchen zählen|2= | ||
<div class="grid"> | |||
<div class="width-3-4">Ihr kennt bereits die verschiedenen geometrischen Figuren. | |||
Heute wollen wir uns mit dem Flächeninhalt von geometrischen Figuren beschäftigen. | |||
Betrachtet dazu die Zeichnungen und ermittelt, | |||
aus wie vielen Kästchen die Rechtecke bestehen. | |||
</div> | |||
<div class="width-1-4"> | |||
[[Bild:UhrPic.jpg|250px|center]] | |||
'''Für diese Aufgabe habt ihr 3 Minuten Zeit!''' | |||
</div> | |||
</div> | |||
<div class="grid"> | <div class="grid"> | ||
| Zeile 38: | Zeile 56: | ||
<br> | <br> | ||
====Hast du richtig gezählt?==== | ====Hast du richtig gezählt?==== | ||
<quiz | <quiz> | ||
{Das Rechteck besteht aus ...} | {Das Rechteck besteht aus ...} | ||
- 16 Kästchen. | - 16 Kästchen. | ||
| Zeile 59: | Zeile 77: | ||
<div class="width-1-3"><span style="background:#63B8FF">3. Rechteck</span> | <div class="width-1-3"><span style="background:#63B8FF">3. Rechteck</span> | ||
[[Bild:Rechteck03.png|right|250px]] | [[Bild:Rechteck03.png|right|250px]] | ||
| Zeile 70: | Zeile 87: | ||
- 8 Kästchen. | - 8 Kästchen. | ||
</quiz> | </quiz> | ||
[[Bild:InfoPic.jpg|center|180px]] | |||
'''Vorsicht: Hier müsst ihr auch die halben Kästchen zählen!!!''' | |||
</div> | </div> | ||
</div> | </div> | ||
| Zeile 75: | Zeile 94: | ||
{{Box|1=3. Arbeitsauftrag - Zeichnen|2= | {{Box|1=3. Arbeitsauftrag - Zeichnen|2= | ||
<div class="grid"> | |||
<div class="width-3-4"> | |||
Zeichnet ein Rechteck in eurem Heft mit Flächeninhalt 16 Kästchen. | Zeichnet ein Rechteck in eurem Heft mit Flächeninhalt 16 Kästchen. | ||
Ihr seht im nächsten Bild 3 verschiedene Rechtecke abgebildet: | Ihr seht im nächsten Bild 3 verschiedene Rechtecke abgebildet: | ||
[[Bild:mehrere Rechtecke.png]] | [[Bild:mehrere Rechtecke.png]] | ||
</div> | |||
<div class="width-1-4">[[Bild:UhrPic.jpg|250px|center]] | |||
'''Für diese Aufgabe habt ihr 5 Minuten Zeit!'''</div> | |||
</div> | |||
Wie ihr leicht sehen könnt, besteht das Rechteck R1 aus 6 Kästchen. Gleichzeitig sind die Seitenlängen des Rechtecks a = c = 3cm | Wie ihr leicht sehen könnt, besteht das Rechteck R1 aus 6 Kästchen. Gleichzeitig sind die Seitenlängen des Rechtecks a = c = 3cm | ||
| Zeile 96: | Zeile 122: | ||
<div class="grid"> | |||
<div class="width-3-4"> | |||
Übertragt die Rechtecke auf Aufgabe 3 in euer Heft. | Übertragt die Rechtecke auf Aufgabe 3 in euer Heft. | ||
Schreibt dabei unter jedes Rechteck die Seitenlängen und den Flächeninhalt. | Schreibt dabei unter jedes Rechteck die Seitenlängen und den Flächeninhalt. | ||
| Zeile 104: | Zeile 130: | ||
immer gleich des Produkts der beiden Seitenlängen ist. | immer gleich des Produkts der beiden Seitenlängen ist. | ||
</div> | |||
<div class="width-1-4">[[Bild:UhrPic.jpg|250px|center]] | |||
'''Für diese Aufgabe habt ihr 10 Minuten Zeit!'''</div> | |||
</div> | |||
Wir notieren: | Wir notieren: | ||
| Zeile 112: | Zeile 143: | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
Daher übertragen wir noch folgenden Satz in unserer Heft | Daher übertragen wir noch folgenden Satz in unserer Heft | ||
| Zeile 124: | Zeile 149: | ||
'''Flächeninhalt des Rechtecks''' | '''Flächeninhalt des Rechtecks''' | ||
#Die Fläche eines Rechtecks ergibt sich aus dem Produkt der Seitenlängen. | #Die Fläche eines Rechtecks ergibt sich aus dem Produkt der Seitenlängen. | ||
#Es gilt also: <math>F = a | #Es gilt also: <math>F = a \cdot b</math> | ||
|Merksatz}} | |Merksatz}} | ||
<div align="left">[[Bild:InfoPic.jpg|250px|center]] | |||
'''Das F steht hier für Flächeninhalt!!!'''</div> | |||
==Ein anschauliches Beispiel== | ==Ein anschauliches Beispiel== | ||
| Zeile 140: | Zeile 168: | ||
Wie könnte man den Flächeninhalt von diesen Figuren berechnen ohne die Kästchen zu zählen? | Wie könnte man den Flächeninhalt von diesen Figuren berechnen ohne die Kästchen zu zählen? | ||
<div class="grid"> | |||
<div class="width-3-4"> | |||
[[Bild:Vieleck1.png]] | |||
</div> | |||
<div class="width-1-4">[[Bild:UhrPic.jpg|250px|center]] | |||
'''Für diese Aufgabe habt ihr 8 Minuten Zeit!'''</div> | |||
</div> | |||
[[Bild:Vieleck2.png]] | [[Bild:Vieleck2.png]] | ||
==Maßeinheiten== | ==Maßeinheiten== | ||
<div class="grid"> | |||
<div class="width-3-4"> | |||
Bisher haben wir uns nur mit der Angabe des Flächeninhalt durch Kästchen beschäftigt. | |||
Nun wollen wir uns mit den Maßeinheiten bei Flächenberechnung beschäftigen. | |||
Dazu wollen wir aber erst einmal die Maßeinheiten der Streckenmessung wiederholen. | |||
</div> | |||
<div class="width-1-4">[[Bild:UhrPic.jpg|250px|center]] | |||
'''Nehmt euch zum Durchlesen der Wiederholung und des Abschnitts "Maßeinheiten beim Flächeninhalt des Rechtecks" 8 Minuten Zeit!'''</div> | |||
</div> | |||
==Wiederholung== | |||
====Wiederholung==== | |||
Ihr kennt bereits: | Ihr kennt bereits: | ||
| Zeile 192: | Zeile 239: | ||
==Maßeinheiten beim Flächeninhalt des Rechtecks== | ====Maßeinheiten beim Flächeninhalt des Rechtecks==== | ||
Betrachten wir nur eine Fläche, zum Beispiel unser lilafarbenes Rechteck von oben. | Betrachten wir nur eine Fläche, zum Beispiel unser lilafarbenes Rechteck von oben. | ||
| Zeile 200: | Zeile 247: | ||
Die Seite b ist 4 cm lang (ebenso die Seite d) | Die Seite b ist 4 cm lang (ebenso die Seite d) | ||
Aus unserer Formel <math>F = a | Aus unserer Formel <math>F = a \cdot b</math> wissen wir, dass hier gilt F = 2 x 4 = 8. Aber welche Einheit ordnen wir nun unserem Rechteck zu? | ||
| Zeile 217: | Zeile 264: | ||
<div>[[Bild:InfoPic.jpg|250px|center]] | |||
'''Man kann nur Seitenlängen mit gleicher Einheit miteinander muliplizieren!!!'''</div> | |||
Es funktioniert also 5cm x 7cm = 35 cm² zu rechnen. Will man hingegen 4cm x 25 mm berechnen, so muss man eine der beiden Einheiten umwandeln. | Es funktioniert also 5cm x 7cm = 35 cm² zu rechnen. Will man hingegen 4cm x 25 mm berechnen, so muss man eine der beiden Einheiten umwandeln. | ||
| Zeile 228: | Zeile 274: | ||
<div>[[Bild:InfoPic.jpg|250px|center]] | |||
'''Die Umrechnungsgrößen sind nicht die gleichen wie bei Streckenlängen!!!'''</div> | |||
Am obigen Beispiel seht ihr sehr gut, dass das Ergebnis des Produkts der Seitenlängen 4cm und 25mm gleich 1000mm² bzw. 10cm² ist. | Am obigen Beispiel seht ihr sehr gut, dass das Ergebnis des Produkts der Seitenlängen 4cm und 25mm gleich 1000mm² bzw. 10cm² ist. | ||
| Zeile 277: | Zeile 318: | ||
|} | |} | ||
=== Aufgaben === | ==== Aufgaben ==== | ||
<div>[[Bild:UhrPic.jpg|250px|center]] | |||
'''Für diese drei Aufgaben habt ihr 10 Minuten Zeit!'''</div> | |||
1. Verwandle in die in Klammern angegebene Einheit. | {{Box|1.Aufgabe| | ||
Verwandle in die in Klammern angegebene Einheit. | |||
a) 8 dm² ( cm² ) | a) 8 dm² ( cm² ) | ||
| Zeile 292: | Zeile 336: | ||
d) 18 cm² ( mm² ) | d) 18 cm² ( mm² ) | ||
|Arbeitsmethode}} | |||
2. Drücke in der in Klammern angegebenen Einheit aus. | |||
{{Box|2.Aufgabe| | |||
Drücke in der in Klammern angegebenen Einheit aus. | |||
a) 3800 cm² ( dm² ) | a) 3800 cm² ( dm² ) | ||
| Zeile 303: | Zeile 351: | ||
d) 25 km² ( cm² ) | d) 25 km² ( cm² ) | ||
|Arbeitsmethode}} | |||
{{Box|1=3.Aufgabe|2= | |||
Berechne jeweils den Flächeninhalt der Rechtecke in einer geeigneten Einheit. | |||
a) b = 5 cm, c = 70 dm | a) b = 5 cm, c = 70 dm | ||
| Zeile 317: | Zeile 368: | ||
f) b = 5 m, c= 200 cm (Gib hier den Flächeninhalt in dm² an.) | f) b = 5 m, c= 200 cm (Gib hier den Flächeninhalt in dm² an.) | ||
|3=Arbeitsmethode}} | |||
==Weitere Arbeitsaufträge== | |||
{{Box|1=5. Arbeitsauftrag - Anwendungsaufgabe Kinderzimmer|2= | {{Box|1=5. Arbeitsauftrag - Anwendungsaufgabe Kinderzimmer|2= | ||
<div class="grid"> | |||
<div class="width-3-4"> | |||
Nora und Paul besichtigen die neue Wohnung, in die sie umziehen wollen. | Nora und Paul besichtigen die neue Wohnung, in die sie umziehen wollen. | ||
| Zeile 328: | Zeile 384: | ||
Nora sagt: "Beide Zimmer sind gleich groß, denn 5 plus 4 ist 9 und 6 plus 3 ist auch 9." | Nora sagt: "Beide Zimmer sind gleich groß, denn 5 plus 4 ist 9 und 6 plus 3 ist auch 9." | ||
Was meinst du? Fertigt für eure Lösung im Heft eine Skizze an. | Was meinst du? Fertigt für eure Lösung im Heft eine Skizze an. | ||
</div> | |||
<div class="width-1-4">[[Bild:UhrPic.jpg|250px|center]] | |||
'''Für diese Aufgabe habt ihr 10 Minuten Zeit!'''</div> | |||
</div> | |||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
| Zeile 335: | Zeile 396: | ||
{{Box|1=6. Arbeitsauftrag - Check dein Wissen|2= | {{Box|1=6. Arbeitsauftrag - Check dein Wissen|2= | ||
<div>[[Bild:UhrPic.jpg|250px|center]] | |||
'''Für diese drei Aufgaben habt ihr 5 Minuten Zeit!'''</div> | |||
<div>[[Bild:InfoPic.jpg|250px|center]] | |||
'''Vorsicht: Ab Frage 7 auch auf Einheiten achten!'''</div> | |||
<quiz | <quiz> | ||
{Wie verändern sich der Flächeninhalt eines Rechtecks, wenn man eine Seitenlänge verdoppelt?} | {Wie verändern sich der Flächeninhalt eines Rechtecks, wenn man eine Seitenlänge verdoppelt?} | ||
- Der Flächeninhalt bleibt gleich. | - Der Flächeninhalt bleibt gleich. | ||
| Zeile 393: | Zeile 456: | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
= | ==Für die ganz Schnellen bzw. für zu Hause== | ||
[[Bild:Haus.jpg]] | |||
Klickt auf den folgenden Link und bearbeitet die Aufgaben zum Flächeninhalt: | Klickt auf den folgenden Link und bearbeitet die Aufgaben zum Flächeninhalt: | ||
* [[../Umfang und Flächeninhalt vom Rechteck|Umfang und Flächeninhalt vom Rechteck]] | * [[../Umfang und Flächeninhalt vom Rechteck|Umfang und Flächeninhalt vom Rechteck]] | ||
| Zeile 423: | Zeile 477: | ||
[[Kategorie:Interaktive Übungen/Mathematik]] | [[Kategorie:Interaktive Übungen/Mathematik]] | ||
[[Kategorie:Koffer gepackt]] | [[Kategorie:Koffer gepackt]] | ||
[[Kategorie:ZUM2Edutags]]<metakeywords>ZUM2Edutags,ZUM-Wiki,Mathematik-digital,Flächeninhalt des Rechtecks,Flächeninhalt,Rechteck,Mathematik,Lernpfad,5. Klasse</metakeywords> | [[Kategorie:ZUM2Edutags]] | ||
<metakeywords>ZUM2Edutags,ZUM-Wiki,Mathematik-digital,Flächeninhalt des Rechtecks,Flächeninhalt,Rechteck,Mathematik,Lernpfad,5. Klasse</metakeywords> | |||
Version vom 10. August 2018, 15:28 Uhr
Zielsetzung:
- Schüler entdecken Schritt für Schritt die Formel des Flächeninhalts und lernen damit zu rechnen.
Altersstufe:
- 5. Jahrgangsstufe am Gymnasium
Zeitbedarf:
- ca. 70 Minuten
Materialen:
- Computer (mit Java und GeoGebra) und Heft.
Arbeitsaufträge
Nun wollen wir zu Beginn erst einmal testen, was ihr denn noch über Vierecke wisst.
Dazu könnt ihr jetzt ein Quiz machen:
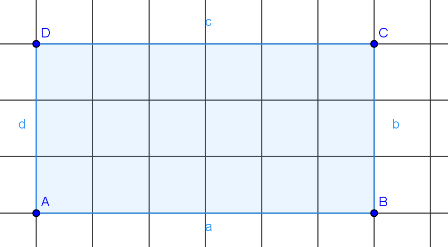
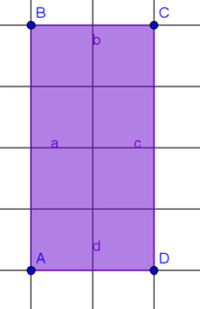
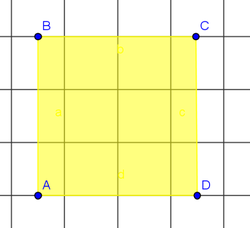
Heute wollen wir uns mit dem Flächeninhalt von geometrischen Figuren beschäftigen.
Betrachtet dazu die Zeichnungen und ermittelt, aus wie vielen Kästchen die Rechtecke bestehen.
Für diese Aufgabe habt ihr 3 Minuten Zeit!
Hast du richtig gezählt?
Hast du richtig gezählt?
Hast du richtig gezählt?
Vorsicht: Hier müsst ihr auch die halben Kästchen zählen!!!
Zeichnet ein Rechteck in eurem Heft mit Flächeninhalt 16 Kästchen.
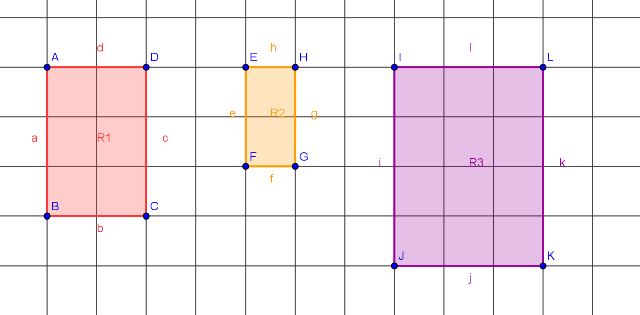
Ihr seht im nächsten Bild 3 verschiedene Rechtecke abgebildet:
Wie ihr leicht sehen könnt, besteht das Rechteck R1 aus 6 Kästchen. Gleichzeitig sind die Seitenlängen des Rechtecks a = c = 3cm
und b = d = 2cm.
Das Rechteck R2 besteht aus 2 Kästchen. Wie sind denn hier die Seitenlängen?
Das Rechteck R3 besteht aus 12 Kästchen. Könnt ihr auch hier die Seitenlängen angeben?
Was fällt euch dabei auf?Übertragt die Rechtecke auf Aufgabe 3 in euer Heft. Schreibt dabei unter jedes Rechteck die Seitenlängen und den Flächeninhalt.
Aus unseren Beobachtungen sehen wir, dass die Anzahl der Kästchen eines Rechtecks
immer gleich des Produkts der beiden Seitenlängen ist.
Wir notieren:
- Im Rechteck R1 haben wir die Seitenlängen a = 2 und b = 3 und der Flächeninhalt beträgt 2 x 3 = 6
- Im Rechteck R2 haben wir die Seitenlängen e = 2 und f = 1 und der Flächeninhalt beträgt 2 x 1 = 2
- Im Rechteck R3 haben wir die Seitenlängen i = 4 und j = 3 und der Flächeninhalt beträgt 4 x 3 = 12
Daher übertragen wir noch folgenden Satz in unserer Heft
Flächeninhalt des Rechtecks
- Die Fläche eines Rechtecks ergibt sich aus dem Produkt der Seitenlängen.
- Es gilt also:
Ein anschauliches Beispiel
Zum Schluss könnt ihr nun noch beobachten, wie sich der Flächeninhalt eines Rechtecks ändert, wenn man die Seitenlängen verändert. Wenn ihr die Punkte der Schieberegler e und f nach links und rechts bewegt, ändert sich auch der Flächeninhalt des Rechtecks.
Andere geometrische Figuren
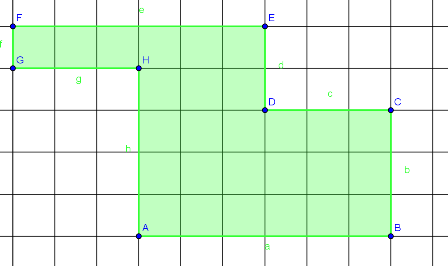
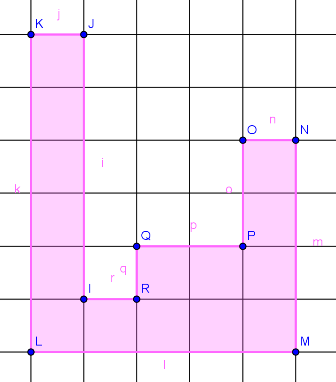
Wie könnte man den Flächeninhalt von diesen Figuren berechnen ohne die Kästchen zu zählen?
Maßeinheiten
Bisher haben wir uns nur mit der Angabe des Flächeninhalt durch Kästchen beschäftigt.
Nun wollen wir uns mit den Maßeinheiten bei Flächenberechnung beschäftigen.
Dazu wollen wir aber erst einmal die Maßeinheiten der Streckenmessung wiederholen.
Wiederholung
Ihr kennt bereits:
| Einheit | kurz | Umrechnung | Grafische Darstellung |
|---|---|---|---|
| Millimeter | mm | 
| |
| Zentimeter | cm | 1 cm = 10 mm | 
|
| Dezimter: dm | dm | 1 dm = 10 cm = 100 mm | 
|
| Meter | m | 1 m = 10 dm = 100 cm = 1000 mm | 
|
| Kilometer | km | 1 km = 1000 m = 10000 dm = 100000 cm = 1000000 mm |
Maßeinheiten beim Flächeninhalt des Rechtecks
Betrachten wir nur eine Fläche, zum Beispiel unser lilafarbenes Rechteck von oben.
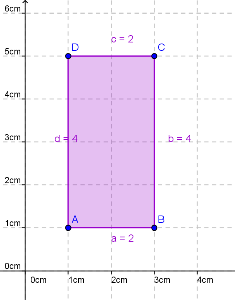
Die Seite a ist 2 cm lang (ebenso die Seite c) Die Seite b ist 4 cm lang (ebenso die Seite d)
Aus unserer Formel wissen wir, dass hier gilt F = 2 x 4 = 8. Aber welche Einheit ordnen wir nun unserem Rechteck zu?
Die Seiten a und b (bzw. c und d) können wir in cm angeben. Aber das Ergebnis, eine Fläche, lässt sich nicht durch cm ausdrücke, da eine Fläche nicht gleich einer Strecke ist!!!
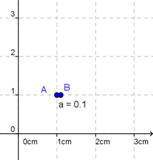
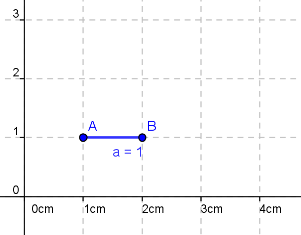
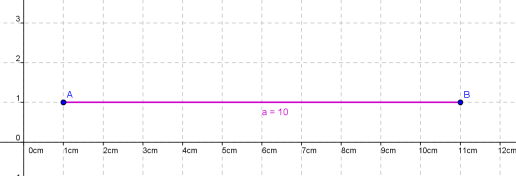
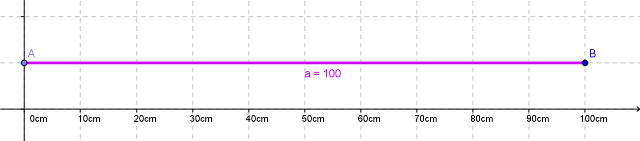
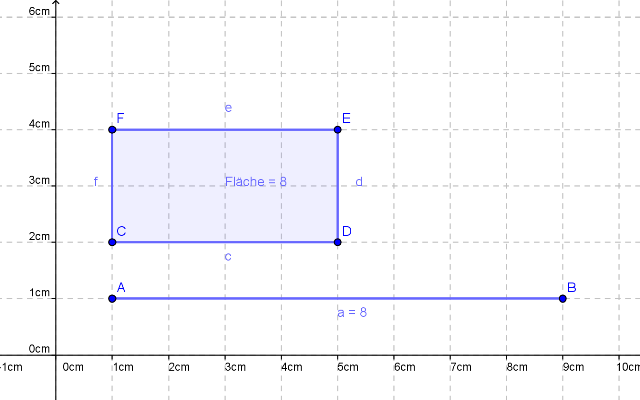
Verdeutlichen wir uns das anhand einer Zeichnung.
Hier seht ihr eine Strecke der Länge 8 cm und ein Rechteck mit Flächeninhalt 8 __ .
An diesem Beispiel könnt ihr erkennen dass die Steckeneinheit "cm" nicht zu der Fläche des Rechtecks passt. Schließlich multiplizieren wir bei einer Fläche ja eine Seitenlänge mit der anderen und rechnen somit auch mm x mm, bzw. cm x cm oder dm x dm ... Daher brauchen wir für die Fläche die Maßeinheiten wie mm², sprich Quadratmillimeter, da wir mm mit mm multiplizieren.
Es funktioniert also 5cm x 7cm = 35 cm² zu rechnen. Will man hingegen 4cm x 25 mm berechnen, so muss man eine der beiden Einheiten umwandeln.
Es bieten sich hier also folgende 2 Möglichkeiten an: 4cm x 25mm = 40mm x 25mm = 1000mm² oder 4cm x 2,5cm = 10cm²
Am obigen Beispiel seht ihr sehr gut, dass das Ergebnis des Produkts der Seitenlängen 4cm und 25mm gleich 1000mm² bzw. 10cm² ist. Die Tabelle oben zeigt, dass 1cm = 10mm ist. Somit ist 1cm² = 1 (cm x cm) = 1x (10mm x 10mm) = 100mm². Ebenso gilt für beispielsweise 2dm² = 2 x (dm x dm) = 2 x (10cm x 10cm) = 2 x (100cm²) = 200 cm² und hierfür gilt wiederum: 200 cm² = 200 x (cm x cm) = 200 x (10mm x 10mm) = 200 x (100mm²) = 20000mm²
Verdeutlichen wir und dies nochmal anhand einer Tabelle:
| Einheit bei Flächen | Produkt | Umrechnung | |
|---|---|---|---|
| Quadratmillimeter | mm x mm = mm² | 1mm² | |
| Zentimeter | cm x cm = cm² | 1cm² = 100mm² | |
| Dezimter: dm | dm x dm = dm² | 1dm² = 100cm² = 10000mm² | |
| Meter | m x m = m² | 1m² = 100dm² = 10000cm² = 1000000mm² | |
| Kilometer | km x km = km² | 1km² = 1000000m² = 100000000dm² = 10000000000cm² = 1000000000000mm² |
Aufgaben
Verwandle in die in Klammern angegebene Einheit.
a) 8 dm² ( cm² )
b) 27 m² ( dm² )
c) 43 km² ( m² )
d) 18 cm² ( mm² )
Drücke in der in Klammern angegebenen Einheit aus.
a) 3800 cm² ( dm² )
b) 5900 dm² ( m² )
c) 470000 m² ( km² )
d) 25 km² ( cm² )
Berechne jeweils den Flächeninhalt der Rechtecke in einer geeigneten Einheit.
a) b = 5 cm, c = 70 dm
b) a = 1200 mm, b = 9 dm
c) c = 5 km, d = 3000 m
d) a = 50 cm, d = 200 mm
e) a = 1200 dm, b = 15 m (Gib hier den Flächeninhalt in cm² an.)
f) b = 5 m, c= 200 cm (Gib hier den Flächeninhalt in dm² an.)Weitere Arbeitsaufträge
Nora und Paul besichtigen die neue Wohnung, in die sie umziehen wollen.
Paul misst die beiden Kinderzimmer aus: Das erste ist 5 m lang und 4 m breit, das zweite 6 m lang und 3 m breit.
Nora sagt: "Beide Zimmer sind gleich groß, denn 5 plus 4 ist 9 und 6 plus 3 ist auch 9."
Was meinst du? Fertigt für eure Lösung im Heft eine Skizze an.
Für die ganz Schnellen bzw. für zu Hause
Klickt auf den folgenden Link und bearbeitet die Aufgaben zum Flächeninhalt:
- [[../Umfang und Flächeninhalt vom Rechteck|Umfang und Flächeninhalt vom Rechteck]]
Vorlage:Mitgewirkt
<metakeywords>ZUM2Edutags,ZUM-Wiki,Mathematik-digital,Flächeninhalt des Rechtecks,Flächeninhalt,Rechteck,Mathematik,Lernpfad,5. Klasse</metakeywords>
