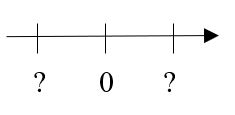Einführung in die Negativen Zahlen: Unterschied zwischen den Versionen
Main>Anto23 Keine Bearbeitungszusammenfassung |
Main>Anto23 Keine Bearbeitungszusammenfassung |
||
| Zeile 6: | Zeile 6: | ||
<b>Voraussetzungen:</b> | <b>Voraussetzungen:</b> | ||
<br> | <br> | ||
*Du kannst natürliche und gebrochene Zahlen am Zahlenstrahl abtragen. | *Du kannst natürliche und gebrochene Zahlen am Zahlenstrahl abtragen. | ||
*Du kannst natürliche und gebrochene Zahlen vergleichen und ordnen. | *Du kannst natürliche und gebrochene Zahlen vergleichen und ordnen. | ||
| Zeile 24: | Zeile 23: | ||
== Didaktische Hinweise für die Lehrkraft == | |||
Dieser Lernpfad ist entsprechend des Lehrplanes in Sachsens zur Einführung der negativen Zahlen im LB 2: "Arbeiten mit rationalen Zahlen" in Klasse 7 angelegt. | |||
==== Vorkenntnisse ==== | |||
Zur Nutzung dieses Lernpfades sind folgende Vorkenntnisse der Schülerinnen und Schüler erforderlich:<br> | |||
*Die SuS können natürliche und gebrochene Zahlen am Zahlenstrahl abtragen. | |||
*Die SuS können natürliche und gebrochene Zahlen vergleichen und ordnen. | |||
<br> | |||
==== Wissensziele ==== | |||
*Die SuS kennen den Alltagsbezug negativer Zahlen. | |||
*Die SuS beherrschen das Darstellen und Ablesen negativer Zahlen an der Zahlengerade. | |||
*Die SuS kennen die Begriffe "entgegengesetzte Zahl" und "Betrag". | |||
*Die SuS können negative Zahlen vergleichen und ordnen. | |||
<br> | |||
==== Einsatz ==== | |||
Die Schülerinnen und Schüler arbeiten alleine oder mit einem Partner. Wenn der Lernpfad in Einzelarbeit durchgeführt wird, kann bei Partnerarbeitsaufgaben die Busstop-Methode eingesetzt werden.<br> | |||
Der Lernpfad ist momentan für ca. 60min konzipiert, wurde aber noch nicht erprobt. | |||
== Technische Hinweise == | |||
Im Laufe des Lernpfades wirst du auf sogenannte Learning Apps treffen. Für eine angenehmere Optik wurden sie manchmal etwas verkleinert. Wenn dir das zu klein ist, kannst du bei jeder Learning App den Vollbild-Modus aktivieren, indem du auf das kleine Symbol oben rechts in dem Applet klickst. | |||
== Einführung == | == Einführung == | ||
| Zeile 37: | Zeile 55: | ||
|- | |- | ||
|valign=top width=50%| | |valign=top width=50%| | ||
{{Aufgabe|{{kommunizieren}}<br> Überlegt gemeinsam, wo uns negative Zahlen im Alltag begegnen. Notiert einige Beispiele auf dem Protokoll und löst dann das Suchsel.}}<br><popup name=" | {{Aufgabe|{{kommunizieren}}<br> Überlegt gemeinsam, wo uns negative Zahlen im Alltag begegnen. Notiert einige Beispiele auf dem Protokoll und löst dann das Suchsel.}}<br><popup name="Hinweise"> | ||
{{Ausblendung | |||
|1=[[Datei:NHP_1879_Berlin_Sternwarte_Skalastein_Tafel_IX.jpg|200px]][[Datei:Kontostand.JPG|200px]] [[Datei:Thermometer im Garten.jpg|200px]] | |||
|2=1. Hinweis | |||
}} | |||
<br> | |||
{{Ausblendung | |||
|1=M_ _ _ _ _ _ _ _ _ _ _ L<br>T_ _ _ _ _ _ _ _ R<br>K _ _ _ _ _ _ _ _ D<br>F _ _ _ _ _ _ _ L | |||
|2=2. Hinweis | |||
}} | |||
</popup> | |||
|width=50%| | |width=50%| | ||
<iframe src="https://learningapps.org/watch?v=pvnt1qzkj18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=pvnt1qzkj18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
| Zeile 55: | Zeile 83: | ||
{|width=100% | {|width=100% | ||
|- | |- | ||
| | |{{Merke| | ||
{{Merke| | |||
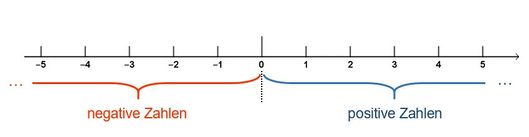
*Zahlen unter Null, wie z.B. am Thermometer oder im Fahrstuhl werden mit einem <b>Minus-Zeichen</b> geschrieben und heißen <b>negative Zahlen</b>. Das Minus-Zeichen ist ein Vorzeichen. | *Zahlen unter Null, wie z.B. am Thermometer oder im Fahrstuhl werden mit einem <b>Minus-Zeichen</b> geschrieben und heißen <b>negative Zahlen</b>. Das Minus-Zeichen ist ein Vorzeichen. | ||
*Zahlen über Null haben ein + als Vorzeichen und heißen <b>positive Zahlen</b>. | *Zahlen über Null haben ein + als Vorzeichen und heißen <b>positive Zahlen</b>. | ||
| Zeile 78: | Zeile 103: | ||
<iframe src="https://learningapps.org/watch?v=pafmickxt18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | <iframe src="https://learningapps.org/watch?v=pafmickxt18" style="border:0px;width:100%;height:500px" webkitallowfullscreen="true" mozallowfullscreen="true"></iframe> | ||
|} | |} | ||
{|width=100% | |||
|- | |||
|width=50%| | |||
{{Merke| | {{Merke| | ||
Wir erweitern unseren bekannten Zahlenstrahl zu einer Zahlengeraden.<br> | Wir erweitern unseren bekannten Zahlenstrahl zu einer Zahlengeraden.<br> | ||
[[Datei:Zahlengerade2.JPG|600px|links]]}} | [[Datei:Zahlengerade2.JPG|600px|links]]}} | ||
|width=50%| | |||
|} | |||
{|width=100% | |||
|- | |||
|width=18%| | |||
{{Übung|Bearbeite die folgenden Aufgaben.}} | |||
|width=82%| | |||
|} | |||
<br> | <br> | ||
<br> | <br> | ||
<b>1. Finde zu jeder Situation eine passende ganze Zahl. Ordne die Situation an die richtige Stelle auf der Zahlengeraden.</b> | <b>1. Finde zu jeder Situation eine passende ganze Zahl. Ordne die Situation an die richtige Stelle auf der Zahlengeraden.</b> | ||
Version vom 28. März 2018, 13:40 Uhr
Didaktische Hinweise für die Lehrkraft
Dieser Lernpfad ist entsprechend des Lehrplanes in Sachsens zur Einführung der negativen Zahlen im LB 2: "Arbeiten mit rationalen Zahlen" in Klasse 7 angelegt.
Vorkenntnisse
Zur Nutzung dieses Lernpfades sind folgende Vorkenntnisse der Schülerinnen und Schüler erforderlich:
- Die SuS können natürliche und gebrochene Zahlen am Zahlenstrahl abtragen.
- Die SuS können natürliche und gebrochene Zahlen vergleichen und ordnen.
Wissensziele
- Die SuS kennen den Alltagsbezug negativer Zahlen.
- Die SuS beherrschen das Darstellen und Ablesen negativer Zahlen an der Zahlengerade.
- Die SuS kennen die Begriffe "entgegengesetzte Zahl" und "Betrag".
- Die SuS können negative Zahlen vergleichen und ordnen.
Einsatz
Die Schülerinnen und Schüler arbeiten alleine oder mit einem Partner. Wenn der Lernpfad in Einzelarbeit durchgeführt wird, kann bei Partnerarbeitsaufgaben die Busstop-Methode eingesetzt werden.
Der Lernpfad ist momentan für ca. 60min konzipiert, wurde aber noch nicht erprobt.
Technische Hinweise
Im Laufe des Lernpfades wirst du auf sogenannte Learning Apps treffen. Für eine angenehmere Optik wurden sie manchmal etwas verkleinert. Wenn dir das zu klein ist, kannst du bei jeder Learning App den Vollbild-Modus aktivieren, indem du auf das kleine Symbol oben rechts in dem Applet klickst.
Einführung
Hier kommt das Video von Powtoon hin.
|
Frage
Was sind negative Zahlen und wo begegnen sie uns im Alltag?
|
|
Aufgabe
Vorlage:Kommunizieren Überlegt gemeinsam, wo uns negative Zahlen im Alltag begegnen. Notiert einige Beispiele auf dem Protokoll und löst dann das Suchsel. <popup name="Hinweise"> Vorlage:Ausblendung
|
|
|
2. Video von Powtoon |
|
Merke
|
Erweiterung der Zahlengeraden
3. Video von Powtoon
|
Frage
Was ist der Unterschied zwischen der 4 unter der Null und der 4 über der Null?
|
|
|
4. Video von Powtoon |
|
|
Übung
Bearbeite die folgenden Aufgaben.
|
1. Finde zu jeder Situation eine passende ganze Zahl. Ordne die Situation an die richtige Stelle auf der Zahlengeraden.
2. Von den beiden folgenden Aufgaben könnt ihr eine auswählen.
|
|
Welche Zahl liegt genau in der Mitte der angegebenen Zahlen? |
Entgegengesetzte Zahlen und Betrag
Welche Zahlen könnt ihr für die Fragezeichen einsetzen? Löst und begründet eure Antwort auf dem Protokoll.
<popup name="Lösungsvorschlag"> Man kann für die Fragezeichen alle Zahlen einsetzen, die sich nur durch das Vorzeichen unterscheiden, also z.B. -3 & 3, -18 & 18, -5 & 5,… , da diese Zahlenpaare denselben Abstand zur 0 haben. </popup>
|
Merke
Zwei Zahlen, die ein entgegengesetztes Vorzeichen, aber zur Null denselben Abstand haben, heißen entgegengesetzte Zahlen. Der Abstand einer Zahl zur 0 heißt Betrag und wird mit Betragsstrichen gekennzeichnet, z.B. <popup name="Weitere Erklärungen zum Betrag"> Der Betrag gibt den Abstand von einer Zahl zur 0 an. Sowohl von der -9 als auch von der 9 muss man 9 Schritte bis zur 0 gehen. Deswegen haben -9 und 9 denselben Abstand, also auch denselben Betrag. Demzufolge ist der Betrag immer positiv, hat also immer ein "+" als Vorzeichen.</popup> |
Ordnen von negativen Zahlen
5. Video von Powtoon
Wem von beiden gebt ihr Recht und warum? Macht zunächst Notizen auf dem Protokoll und tauscht euch dann mit dem Partner aus.
<popup name="Lösung und Erklärung">-4 ist kleiner als -1.
Vielleicht hat einer von euch argumentiert, dass doch aber bei -4°C die Kälte größer ist oder 4€ Schulden mehr als 1€ Schulden sind. Das ist prinzipiell auch nicht verkehrt. In der Mathematik jedoch werden häufig Regeln festgelegt, damit es logisch bleibt. Leider passen diese Regeln dann aber nicht immer in unser Alltagsdenken. Man hat sich also entschieden, dass Zahlen kleiner sind je weiter links sie auf der Zahlengeraden liegen, so wie das auch bei den positiven Zahlen ist. Das hat folgenden Grund:
Von den positiven Zahlen wissen wir:
11 > 8.
Nun ziehen wir links und rechts immer 4 ab:
7 > 4
3 > 0
-1 > -4
Wenn wir davon ausgehen, dass -4 größer wäre als -1, dann würde sich das Relationszeichen umdrehen und das wäre nicht logisch. </popup>
Im Folgenden findet ihr 10 Aufgaben, die mit Sternchen markiert sind. Ihr könnt auswählen, welche Aufgaben ihr bearbeiten wollt. Wichtig ist nur, dass ihr min. 8 Sternchen sammelt.
Aufgabe 1-4: *
Aufgabe 5-8: **
|
*1. Ordne die Aufgaben zu dem richtigen Relationszeichen zu. |
*2. Ordne die Aufgaben zu dem richtigen Relationszeichen zu. | ||||||||||||||||||
|
|
|||||||||||||||||||
|
*3. Ordne die Zahlen der Größen nach. |
*4. In den Niederlanden liegt rund ein Viertel der Gesamtfläche unter dem Meeresspiegel. In der folgenden Tabelle findest du die Höhenangaben für einige Städte.Schreibe sie in eine mathematische Schreibweise und ordne sie der Größe nach. | ||||||||||||||||||
|
|
|
|
**5. Setze für den Strich eine Ziffer so ein, dass die Aussage stimmt. |
**6.Gib vier Zahlen an, für die folgendes gilt: |
|
**7. Erstelle eine Beschreibung für die folgenden Zahlen.
|
Vorlage:Kommunizieren
**8. Nimm Stellung zu folgenden Schüleräußerungen: |
|
***9. Begründe mit Hilfe der Zahlengeraden oder widerlege mit einem Gegenbeispiel. |
***10.
b) Erfinde selbst so ein Zahlenrätsel und gib es deinem Partner zum Lösen.
|