Einführung in quadratische Funktionen/Übungen 3: Unterschied zwischen den Versionen
Main>Reinhard Schmidt Keine Bearbeitungszusammenfassung |
Main>Andrea Schellmann (inhalt von Abschlusstestseite eingefügt) |
||
| Zeile 51: | Zeile 51: | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
'''f(x) = –2x<sup>2</sup> + 3x – 4''' (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt | '''f(x) = –2x<sup>2</sup> + 3x – 4''' (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt \!\,(\!\,2|-6] liegt auf dem Graphen.) (Der Punkt [1|1] liegt nicht auf dem Graphen.) | ||
| Zeile 98: | Zeile 98: | ||
|} | |} | ||
</div> | </div> | ||
== Interaktive Übungen == | |||
*[http://www.mathe-online.at/galerie/fun1/funscribble/index.html Zeichne den Graphen] | |||
*[http://www.zum.de/dwu/depothp/hp-math/hpmqf12.htm Übung 1] | |||
---- | ---- | ||
{| | | ||
{{Autoren|[[Benutzer:Reinhard Schmidt|Reinhard Schmidt]], [[Benutzer:Christian Schmidt|Christian Schmidt]], [[Benutzer:Maria Eirich|Maria Eirich]], [[Benutzer:Andrea Schellmann|Andrea Schellmann]]}} | |||
[[ | |||
Version vom 1. April 2009, 19:21 Uhr
Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Allgemeine quadratische Funktion - Übungen 3 - Abschlusstest
Aufgabe 1: Funktionsterm finden
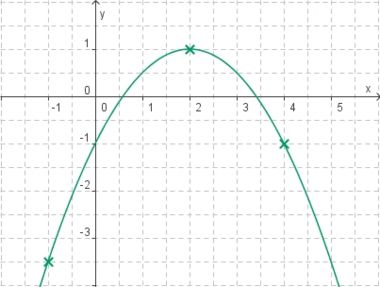
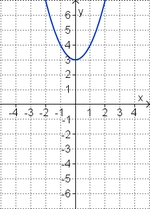
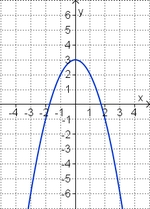
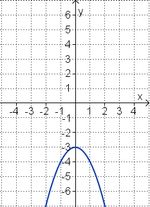
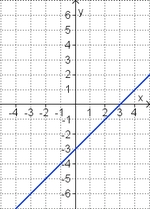
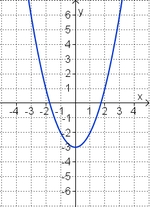
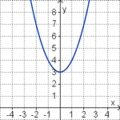
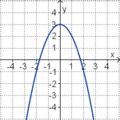
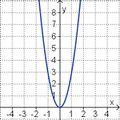
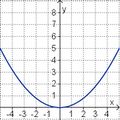
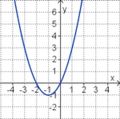
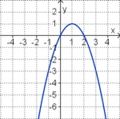
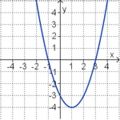
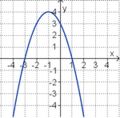
Aufgabe 2: Term und Graph zuordnen Ordne den Funktionsgraphen den richtigen Term zu.
Aufgabe 3: Multiple Choice Kreuze jeweils alle richtigen Aussagen an. f(x) = –2x2 + 3x – 4 (Die Parabel ist nach unten geöffnet.) (!Die Parabel ist nach oben geöffnet.) (Die Parabel ist enger als die Normalparabel.) (!Die Parabel ist weiter als die Normalparabel.) (Der Punkt \!\,(\!\,2|-6] liegt auf dem Graphen.) (Der Punkt [1|1] liegt nicht auf dem Graphen.)
Aufgabe 4: Memo-Quiz Finde die richtigen Paare - je ein Funktionsterm und ein Funktionsgraph gehören zusammen. Achte auf die wesentlichen Eigenschaften der Funktion (Öffnung der Parabel, Lage des Scheitels, Nullstellen).
Interaktive Übungen
|