Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Einführung in quadratische Funktionen/Übungen 2: Unterschied zwischen den Versionen
Main>Reinhard Schmidt Keine Bearbeitungszusammenfassung |
Main>Reinhard Schmidt Keine Bearbeitungszusammenfassung |
||
| Zeile 9: | Zeile 9: | ||
|- | |- | ||
|<div style="padding:10px;background:#ffffff;border:1px ;"> | |<div style="padding:10px;background:#ffffff;border:1px ;"> | ||
<big>''' | <big>'''Aufgabe 1: Anhalteweg'''</big> | ||
Die Funktion '''s(v) = 0,1v<sup>2</sup> + 1,5v''' ist ein Beispiel für eine Funktion, die den Zusammenhang zwischen der anfänglichen Geschwindigkeit eines Fahrzeuges in m/s und dem Anhalteweg für einen konkreten Bremsvorgang angibt. | Die Funktion '''s(v) = 0,1v<sup>2</sup> + 1,5v''' ist ein Beispiel für eine Funktion, die den Zusammenhang zwischen der anfänglichen Geschwindigkeit eines Fahrzeuges in m/s und dem Anhalteweg für einen konkreten Bremsvorgang angibt. | ||
| Zeile 34: | Zeile 34: | ||
|- | |- | ||
|<div style="padding:10px;background:#ffffff;border:1px ;"> | |<div style="padding:10px;background:#ffffff;border:1px ;"> | ||
<big>''' | <big>'''Aufgabe 2: Bestimme a und b'''</big> | ||
{| | {| | ||
| Zeile 71: | Zeile 71: | ||
<div style="padding:10px;background:#ffffff;border:1px grey;"> | <div style="padding:10px;background:#ffffff;border:1px grey;"> | ||
<big>''' | <big>'''Aufgabe 3: Term und Graph zuordnen'''</big> | ||
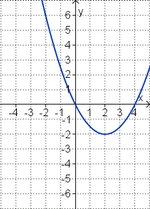
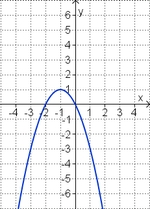
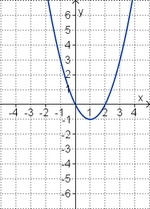
'''Ordne den Funktionsgraphen den richtigen Term zu.''' | '''Ordne den Funktionsgraphen den richtigen Term zu.''' | ||
| Zeile 87: | Zeile 87: | ||
{| | {| | ||
<div style="padding:10px;background:#ffffff;border:1px grey;"> | <div style="padding:10px;background:#ffffff;border:1px grey;"> | ||
<big>''' | <big>'''Aufgabe 4'''</big> | ||
'''Kreuze jeweils alle richtigen Aussagen an.''' | '''Kreuze jeweils alle richtigen Aussagen an.''' | ||
Version vom 29. März 2009, 07:24 Uhr
Einführung - Bremsweg - Unterschiedliche Straßenverhältnisse - Übungen 1 - Anhalteweg - Übungen 2 - Allgemeine quadratische Funktion - Übungen 3 - Abschlusstest
Aufgabe 1: Anhalteweg Die Funktion s(v) = 0,1v2 + 1,5v ist ein Beispiel für eine Funktion, die den Zusammenhang zwischen der anfänglichen Geschwindigkeit eines Fahrzeuges in m/s und dem Anhalteweg für einen konkreten Bremsvorgang angibt.
|
Aufgabe 2: Bestimme a und b
|
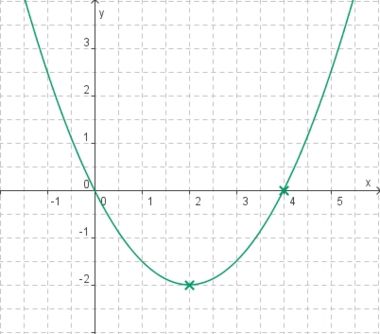
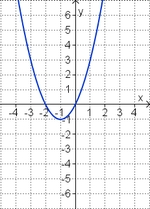
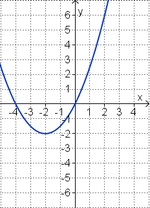
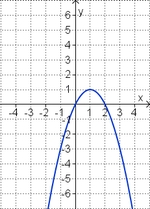
Aufgabe 3: Term und Graph zuordnen
Ordne den Funktionsgraphen den richtigen Term zu.
Aufgabe 4
Kreuze jeweils alle richtigen Aussagen an.
<b>f <b>Welche der Termpaare gehören zu Funktionen, deren Graphen bezüglich der y-Achse symmetrisch zueinander sind?</b> <b>f |