Diagramme auswerten und interpretieren/Dreiecksdiagramm

Kurzinfo

Hier lernst Du eine neue Diagrammform kennen und zu interpretieren. Man nennt diese Diagrammform Dreiecksdiagramm. Diese Art von Diagrammen sind in den Fächern Wirtschaft, Geographie (Geologie) und Chemie übliche Darstellungen}}

Einführung

Um die Abhängigkeit von zwei Größen in einem Diagramm darzustellen benutzt man üblicherweise ein x-y-Koordinatensystem. In vielen Fällen hängen aber drei auch mehr Größen voneinander ab. Speziell für drei Größen wie z.B.

• den primären, sekundären und tertiären Wirtschaftssektor oder
• die Anteile von Feldspat, Quarz und Glimmer in magmatischen Gesteinen
  

ist das sogenannte Dreiecksdiagramm eine übliche Darstellung.

Im folgenden Diagramm ist der Prozentanteil an Vollerwerbslandwirten, Zuerwerbslandwirten und Nebenerwerbslandwirten in der Bundesrepublik dargestellt.

Zur Begriffsklärung:

• Vollerwerbslandwirt: erzielt sein Einkommen zu 100 % aus der Landwirtschaft
• Zuerwerbslandwirt: der Anteil des Einkommens aus der Landwirtschaft beträgt mehr als 50 %
• Nebenerwerbslandwirt: der Anteil des Einkommens aus der Landwirtschaft beträgt weniger als 50 %

Ablesen von Werten im Dreiecksdiagramm

Merksatz

• Das Dreiecksdiagramm ist (üblicherweise ein gleichseitiges Dreieck) ein Diagramm, in dem man von drei Größen die Prozentanteile an der Summe der einzelnen Größen darstellt.
• In jedem Punkt ergibt sich als Summe der Prozentwerte der einzelnen Größen 100 %.
• Die Prozentanteile der einzelnen Größen liest man an den Parallele durch den Datenpunkt zur jeweils übernächsten Seite (gegen den Uhrzeigersinn) ab oder einfacher: vom Datenpunkt zu den Seiten des Dreiecks längs der Gitternetzlinien.
• Die Werte in einem Dreiecksdiagramm gestatten keinen Rückschluss auf Absolutwerte der einzelnen Größen. }}

Üben

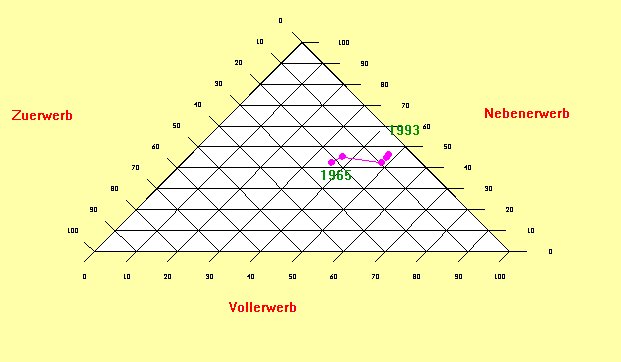
Übung zum Ablesen Anteil der in der Lw. Besch. nach Erwerbscharakter für die Jahre 1965, 1970, 1980, 1990 und 1993

1 Frage 1: Wie hoch war der Anteil der Vollerwerbslandwirte 1965?

	ca. 22 %
	ca. 37 %
	ca. 41 %

2 Frage 2: Wie hoch war der Anteil der Zuerwerbslandwirte in Deutschland 1965?

	ca 22 %
	ca.37 %
	ca 41 %

Üben

• Erstelle eine Tabelle für die Anteile der landwirtschaftlichen Voll-, Zu- und Nebenwerwerbsbetriebe in Deutschland aus dem Dreiecksdiagramm.
• Erstelle mittels eines Tabellenkalkulationsprogram aus der Tabelle verschiedene sinnvolle Diagramme.
• Überlege, weshalb es trotzdem sinnvoll ist, dass man manche Daten in einem Dreiecksdiagramm darstellt.

<popup> Lösung Datei:Tabauswertung2.xls </popup>

Merksatz

Bei der Darstellung einer zeitlichen Entwicklung kann man die Abhängikeit der drei Größen voneinander untersuchen. Ist die Kurve weitgehend (oder in Teilen) parallel zu einer der drei Seiten, so hat eine der drei Größen einen konstanten (im betrachteten Zeitraum konstanten) Anteil. Voneinander abhängig sind nur die beiden anderen Größen.

Erstellung eines Dreiecksdiagrammes

Üben

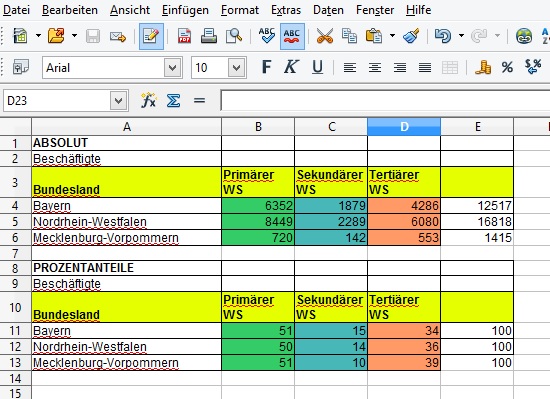
Umsetzen einer Tabelle in ein Dreiecksdiagramm |2=

Beschäftigte in 1000 im Jahr 2003
Bundesland	Primärer WS	Sekundärer WS	Tertiärer WS
Bayern	6352	1879	4286
Nordrhein-Westfalen	8449	2289	6080
Mecklenburg-Vorpommern	720	142	553

Vorlage zum Ausdrucken

Setze die obige Tabelle in ein Dreiecksdiagramm um.

Hilfe:

• Berechne die Summe aus den einzelnen Wirtschaftssektoren der jeweiligen Bundesländer
• Berechne die jeweiligen Prozentanteile der einzelnen Wirtschaftssektoren in den einzelnen Bundesländern

Das kannst Du mit dem Taschenrechner oder auch mit einem Tabellenkalkulationsprogramm machen.

Tabellenkalkulation

• Drucke Dir für das Einzeichnen das rechts oben abgebildete Dreiecksdiagramm aus und trage die Datenpunkte ein.

}}

Vorlage:Schrift grünn

Nun betrachten wir ein anderes Dreiecksgidagramm:

Erläuterung der Begriffe:

In der Geologie, der Bodenkunde aber auch im Baustoffhandel unterscheiden man verschiedene Korngrößen. Dafür gibt es die sog. DIN 4022:

Da in Böden nicht nur ein Korngröße vertreten ist (Wir erforschen den Boden, beschreibt man die sog. Bodenart durch die Prozentanteile der drei Korngrößengruppen Ton, Schluff und Sand. Je nach der Lage im Dreiecksdiagramm (nicht vollständige Begriffsdefinition) kennzeichnet man in Beschreibungen die Bodenart als schluffig sandigen Lehm, als lehmigen Sand, tonigen Schluff usw.

Vorlage:Aufgaben-blau

Vorlage:Schrift grün

Vorlage:Aufgaben-blau

Merke

Interpretieren des Diagrammes bedeutet das Verknüpfen der Daten des Diagrammes mit anderen Quellen, wie z.B. einem vorgegebenem Text, dem Atlas oder weiteren (anderen) Diagrammen. Es bedeutet Gründe für die zeitliche Entwicklung zu finden oder z. B. Gründe für die unterschiedlichen Anteile in den einzelnen Ländern zu finden.

<popup name="Eine mögliche Lösung"></popup>