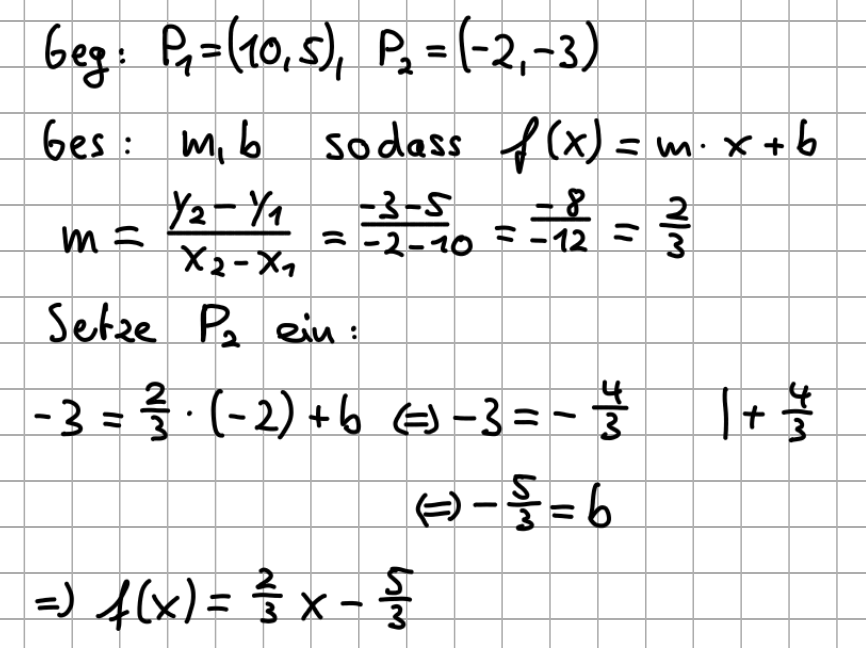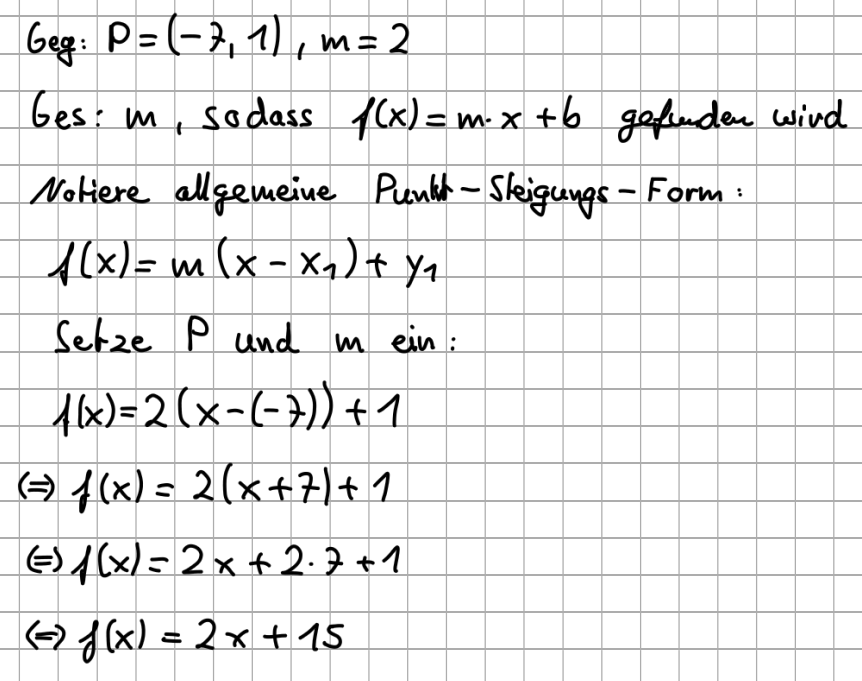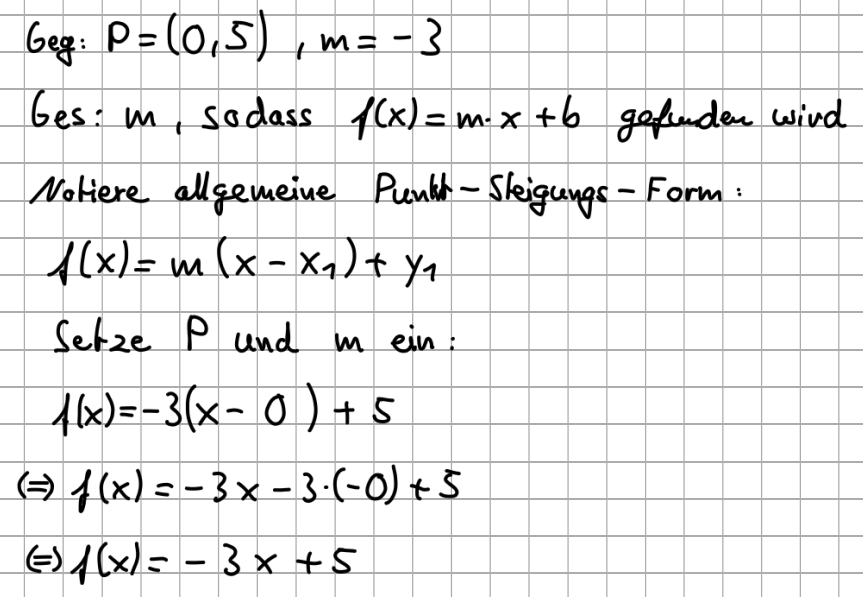Benutzer:Pascal Königstein/Wiederholung lineare Funktionen

Willkommen zum Lernpfad "Wiederholung lineare Funktionen"

Dieser Lernpfad ist für 4 Unterrichtsstunden konzipiert und dient dazu das Thema "lineare Funktionen" für den Einstieg in die Analysis der gymnasialen Oberstufe zu wiederholen. Er ist so gedacht, dass Sie sich durch die Themen systematisch durcharbeiten und je nach Wiederholungsbedarf diese Themen erneut aufarbeiten.

Intendiertes Ziel des Lernpfades ist es, den Umgang mit symbolisch-technischen Elementen der Mathematik im Bereich der Analysis zu verbessern.

Begriff der linearen Funktion

In diesem Kapitel werden die grundlegenden Eigenschaften einer linearen Funktion geklärt und die Parameter der Funktionsgleichung definiert.

Funktionsgleichung

Die allgemeine Funktionsgleichung einer linearen Funktion

Eine lineare Funktion besitzt eine Gleichung der Form y = m*x + b. In der gymnasialen Oberstufe verwendet man oft anstelle des "y" das "f(x)" (gesprochen: "f von x"). Beide Ausdrücke meinen dabei das Gleiche, also den Funktionswert an der Stelle x.

Aufgabe:

Entscheide, welche der folgenden Funktionsgleichung eine Funktionsgleichung einer linearen Funktion ist.

1) y = 3x + 4

Schaue dir die allgemeine Form an und versuche die Parameter m und b in der Funktionsgleichung von 1) zu identifizieren.

Die Funktionsgleichung ist eine lineare Funktion. Der Parameter m ist hier 3 und b ist 4. Die Funktionsgleichung besitzt also die Form der allgemeinen Funktionsgleichung einer linearen Funktion.

2) y = (7/2)x - 9/5

Dich verunsichern die Brüche? Brüche sind ebenfalls "nur" Zahlen. Kannst du die Brüche als Dezimalbruch (Kommazahl) darstellen und sie dann mit den Parametern m und b identifizieren?

Die Funktionsgleichung ist eine lineare Funktion. Der Parameter m ist hier 7/2 und b ist -9/5. Die Funktionsgleichung besitzt also die Form der allgemeinen Funktionsgleichung einer linearen Funktion.

3) y² = 20x + 4

Betrachte beide "Seiten" der Funktionsgleichung und vergleiche genauer y, m, x und b mit der allgemeinen Funktionsgleichung.

Diese Funktionsgleichung ist keine lineare Funktion! Bei dem y ist ein Exponent, welcher ungleich 1 ist (nämlich hier 2). Würde man die Wurzel auf beiden Seiten ziehen, steht links zwar dann y, allerdings würde die rechte Seite die Wurzel aus x abbilden. Die Funktionsgleichung gehört dann also zu einer Wurzelfunktion!

4) x + 3 = y

Überlege, ob man die beiden Seiten einer Gleichung tauschen darf.

Auch die Gleichung von 4) ist eine lineare Funktion. Es ist mathematisch völlig egal, ob man die Seiten einer Gleichung tauscht oder nicht.

5) y = -5x² - 9

Betrachte beide "Seiten" der Funktionsgleichung und vergleiche genauer y, m, x und b mit der allgemeinen Funktionsgleichung.

Bei dem x ist der Exponent nicht 1 sondern 2. Es handelt sich also nicht um eine lineare, sondern um eine quadratische Funktion.

6) y = x

Die Parameter m und b können alle reelle Zahlen sein!

Die Parameter m und b der linearen Funktion können alle reelle Zahlen sein, also auch 0. In diesem Beispiel ist m $=$ 1 und b $=$ 0. Es steht dort also y $=$ 1*x + 0 oder in kürzer: y $=$ x.

7) y = -3

Welche Überlegungen hast du bei Gleichung 6) gemacht?

Die Parameter m und b der linearen Funktion können alle reelle Zahlen sein, also auch 0. In diesem Beispiel ist m $=$ 0 und b $=$ -3. Es steht dort also y $=$ 0*x + (-3) oder in kürzer: y $=$ -3.

8) y = $\pi$

Überlege genauer: Was ist "$\pi$"?

Siehe dir die Hilfen zu den Gleichungen 6) und 7) an.

In diesem Beispiel ist m $=$ 0 und b $=$ $\pi$. Da $\pi$ $\thickapprox$ 3,141 lediglich eine reelle Zahl ist, haben wir eine gleiche Situation wie bei Gleichung 7), nur dass wir anstatt der -3 die irrationale Zahl $\pi$ haben.

Bedeutung der Parameter m und b

In diesem Kapitel schauen wir uns die beiden Parameter m und b der allgemeine Gleichung einer linearen Funktion an.

Wie beeinflussen die beiden Parameter die Lage des Graphen der Funktionsgleichung? Was passiert wenn ich diese variiere?

Wenn du dir schon sehr sicher bist, gehe zum Pfad "Experte", wenn du an manchen Stellen noch etwas unsicher bist, benutze den Pfad "Fortgeschritten".

Experte

Beantworte folgende Fragen schriftlich mit Hilfe der untenstehenden GeoGebra-Umgebung und vergleiche deine Ergebnisse mit den Lösungen am Ende:

1. Beschreibe die Lage (das "Aussehen") des Graphen, wenn man die Steigung m im Bereich von 0 $<$ m wählt bzw. verändert.
2. Beschreibe die Lage (das "Aussehen") des Graphen, wenn man die Steigung m im Bereich von 0 $>$ m wählt bzw. verändert.
3. Beschreibe die Lage (das "Aussehen") des Graphen, wenn man die Steigung m $=$ 0 wählt/einstellt.
4. Wie verändert sich die Lage (das "Aussehen") des Graphen, wenn man den y- Achsenabschnitt b verändert? Schreibe als je-desto-Satz.

Hat die Funktionsgleichung eine positive Steigung (0 $<$ m), so verläuft die Gerade von unten links nach oben rechts.

Hat die Funktionsgleichung eine negative Steigung (0 $>$ m), so verläuft die Gerade von oben links nach unten rechts.

Hat die Funktionsgleichung die Steigung m $=$ 0, so verläuft die Gerade horizontal, also parallel zur x-Achse (zur horizontalen Achse).

Erhöht (verringert) man den y-Achsenabschnitt b, so verschiebt sich die Gerade nach oben (nach unten). Je höher der y-Achsenabschnitt b ist, desto weiter oben verläuft die Gerade im Koordinatensystem. Je niedriger der y-Achsenabschnitt b ist, desto niedriger verläuft die Gerade im Koordinatensystem.

Fortgeschritten

Schreibe die folgenden Merksätze ab und fülle die Lücken mit Hilfe der untenstehenden GeoGebra-Umgebung aus. Vergleiche deine Ergebnisse mit den Lösungen am Ende:

1) Hat die Funktionsgleichung eine (?) Steigung (0 $<$ m), so verläuft die Gerade von unten (?) nach oben (?).

2) Hat die Funktionsgleichung eine negative Steigung (0 (?) m), so verläuft die Gerade von (?) links nach (?) rechts.

3) Hat die Funktionsgleichung die Steigung m $=$ (?), so verläuft die Gerade horizontal, also parallel zur (?)-Achse (zur horizontalen Achse).

4) (?) (verringert) man den y-Achsenabschnitt b, so verschiebt sich die Gerade nach oben ((?)). Je (?) der y-Achsenabschnitt b ist, desto weiter oben verläuft die Gerade im Koordinatensystem. Je (?) der y-Achsenabschnitt b ist, desto niedriger verläuft die Gerade im Koordinatensystem.

Hat die Funktionsgleichung eine positive Steigung (0 $<$ m), so verläuft die Gerade von unten links nach oben rechts.

Hat die Funktionsgleichung eine negative Steigung (0 $>$ m), so verläuft die Gerade von oben links nach unten rechts.

Hat die Funktionsgleichung die Steigung m $=$ 0, so verläuft die Gerade horizontal, also parallel zur x-Achse (zur horizontalen Achse).

Erhöht (verringert) man den y-Achsenabschnitt b, so verschiebt sich die Gerade nach oben (nach unten). Je höher der y-Achsenabschnitt b ist, desto weiter oben verläuft die Gerade im Koordinatensystem. Je niedriger der y-Achsenabschnitt b ist, desto niedriger verläuft die Gerade im Koordinatensystem.

Darstellungsformen

Lineare Funktionen lassen sich auf verschiedene Art und Weisen darstellen. Du kennst bereits die typischen Darstellungsweisen einer linearen Funktion, deswegen geht es sofort mit einer kleinen Aufgabe los.

AUFGABE: In der folgenden Tabelle fehlen die Definition und ein Beispiel für die Darstellungsweisen von Funktionen. Ordne die beispielhaften Darstellungsweisen von Funktionen dem richtigen Funktionsbegriff zu und formuliere eine passende Definition. Falls du nicht weiter kommst oder nochmal nachschauen möchtest findest du in den Hilfekarten die Definition der jeweiligen Begriffe.

algebraisch	tabellarisch	grafisch

Beispielhafte Darstellungsweisen von Funktionen
f(x) = 5x + 6

Die algebraische Darstellungsweise legt die Berechnung der Funktionswerte fest. Dies erfolgt i.d.R. durch eine Gleichung.

In einer (Werte-)Tabelle werden die Funktionswerte von ausgewählten Stellen der Funktion festgehalten.

Die eindeutige Zuordnung zwischen Stellen und Funktionswerten wird für einen ausgewählten Bereich in Form eines Graphen dargestellt.

Wertetabelle

Die Darstellung von linearen Funktionen in Wertetabellen

In einer (Werte-)Tabelle werden die Funktionswerte von ausgewählten Stellen der Funktion festgehalten. Der Funktionswert an der Stelle 0 gibt dabei den y-Achsenabschnitt an. Die Steigung kann aus der Veränderung des Funktionswertes von zwei aufeinanderfolgenden Stellen bestimmt werden.

AUFGABE:

Welche Funktionsvorschrift ist Grundlage der folgenden Wertetabellen? Beschreibe zunächst in Worten und gib falls möglich die Gleichung an.

3x+4

-2x+1

-0,75x+3

Graphische Darstellung im kartesischen Koordinatensystem

Die grafische Darstellung einer linearen Funktion kann mithilfe der Funktionsgleichung oder einer Wertetabelle erfolgen.

WERTETABELLE: Bei einer Wertetabelle werden mindestens zwei Punkte aus der Wertetabelle im Koordinatensystem eingetragen und anschließend zu einer Geraden verbunden. Geschickterweise nutzt man eine möglichst kleine Stelle und eine möglichst große Stelle aus der Wertetabelle.

FUNKTIONSGLEICHUNG: Bei einer Funktionsgleichung trägt man zuerst den y-Achsenabschnitt b im Koordinatensystem ein. Anschließend kann man eine Stelle mit entsprechend großem Abstand zur Stelle 0 in die Gleichung einsetzen und den Funktionswert berechnen und im Koordinatensystem eintragen. Diese zwei Punkte werden anschließend verbunden. Alternativ kann man sich mithilfe der Funktionsgleichung überlegen, wie groß die Steigung m der Funktion ist und ausgehend vom y-Achsenabschnitt den nächsten Punkt einzeichnen. Auch diese zwei Punkte werden anschließend verbunden. Je nach Steigung der Funktion ist der zweite Weg etwas ungenauer.

AUFGABE:

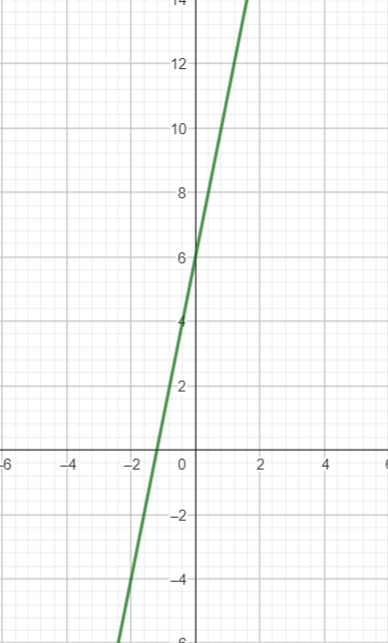
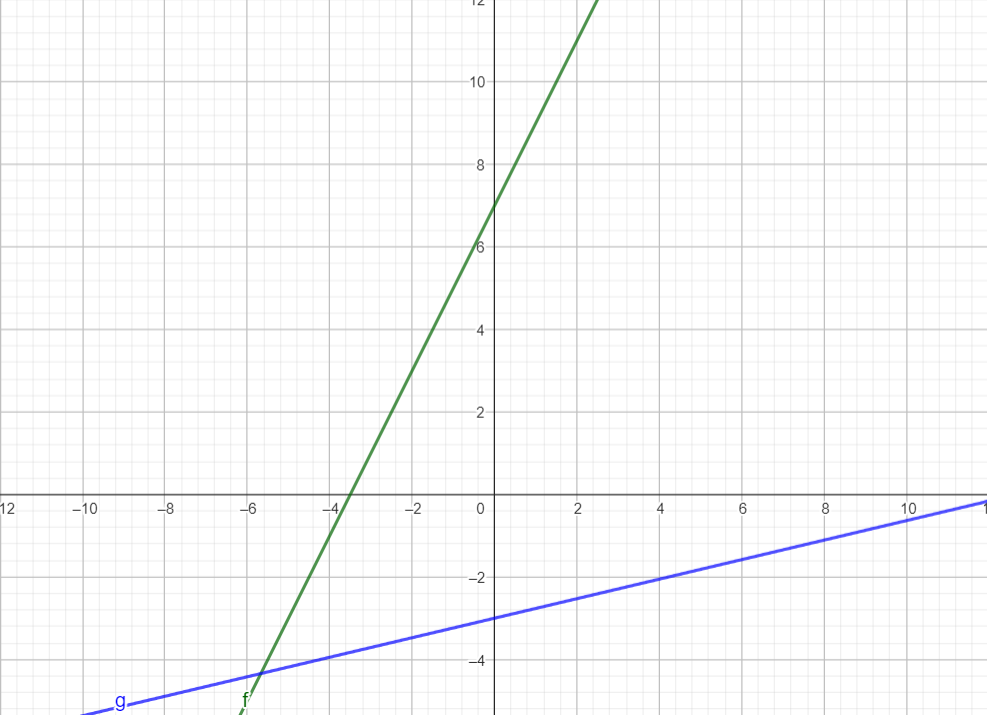
Stelle die Funktionen f(x)=2x+7 und g(x)=0,23667x-3 grafisch dar. Überlege dir welche der beiden aufgezeigten Vorgensweisen zur grafischen Darstellung von Funktionsgleichungen sinnvoller ist.

Die Funktionsgleichung f(x) ist einfacher mit der ersten Methode darstellbar und die Funktionsgleichung g(x) ist nur mit der zweiten Methode genau darstellbar.

Ablesen von Steigung und y-Achsenabschnitt

Das Ablesen von Steigung und y-Achsenabschnitt ist zentral bei der Arbeit mit den Graphen linearer Funktionen. Wie gut kannst du dich daran erinnern, wie das funktionierte? Wenn du dir noch ziemlich sicher bist kannst du die Expertenversion bearbeiten. Wenn du dir eher unsicher bist bearbeite vielleicht lieber die Forgeschrittenenversion.

Notiere dir den richtigen Merksatz nach der Bearbeitung der Aufgabe in deinem Heft.

Experte

Weißt du noch, wie man Steigung und y-Achsenabschnitt einer linearen Funktion bestimmt?

Fortgeschritten

Weißt du noch, wie man Steigung und y-Achsenabschnitt einer linearen Funktion bestimmt?

Zusammenhang zwischen Graph und Funktionsgleichung

Das Erkennen des Zusammenhangs zwischen Graph und Funktionsgleichung ist Übungssache und wird in der Oberstufe noch sehr wichtig. Lust auf ein bisschen Training?

Berechnungen an linearen Funktionen

Wir wissen nun was eine lineare Funktion ist, welche Bedeutung die Parameter m und b haben, wie man lineare Funktionen darstellen kann und welche Beziehungen diese Darstellungen zueinander haben.

Nun starten wir mit dem Rechnen mit den Funktionsgleichungen. Zunächst wiederholen wir, wie man eine Funktionsgleichung entweder aus zwei Punkten oder aus einem Punkt und der Steigung m erhalten, bevor wir uns die Schnittpunkte mit den Koordinatenachsen näher anschauen.

Bestimmung der Funktionsgleichung aus zwei Punkten (Zwei-Punkte-Form)

Um die Gleichung einer linearen Funktion aus gegebene Informationen zu berechnen gilt folgender Zusammenhang:

Die allgemeine lineare Funktion besitzt die Form y $=$ m*x + b. Wir haben also zwei unbekannte Parameter. Um diese genau bestimmen und berechnen zu können, benötigen wir zwei voneinander verschiedene Eigenschaften der Funktion, die diese beschreiben. Die erste Möglichkeit ist die Berechnung von m und b durch zwei voneinander verschiedene Punkte, welche auf dem Graphen der linearen Funktion liegen. Um sich dies wieder ins Gedächtnis zu rufen bearbeite dazu die folgenden beiden Aufgaben.

Schaue dir das folgende Video an und bearbeite die folgenden Aufgaben.

1. Schaue dir den gleichen Videoabschnitt noch einmal an und notiere dir schriftlich was bei der Berechnung der Gleichung einer linearen Funktion gegeben und gesucht ist, sowie die zentralen Schritte und wichtigsten Formeln.
2. Vergleiche mit der Lösung.

Gegeben: Zwei voneinander verschiedene Punkte auf der Geraden der gesuchten Funktion. Gesucht: m und b, sodass die Funktionsgleichung f(x)$=$m*x+b gefunden wird. Vorgehen: 1) Berechne die Steigung m mit Hilfe der Formel des Differenzenquotienten $m = {y_2-y_1 \over x_2-x_1}$. 2) Berechne b, indem du den x und y- (bzw. f(x)-) Wert eines Punktes (aber nicht den y-Achsenabschnitt!) sowie die gefundene Steigung in die allgemeine Form (y $=$ m*x + b) einsetzt und nach b umformst.

3) Schreibe die "fertige" Gleichung mit den berechneten m und b als Lösung auf.

Aufgabe: Berechne die Funktionsgleichung mit der Form f(x)$=$m*x+b aus den beiden gegebene Punkten schriftlich.

a) $P_1 = \bigl(1,3)$ und $P_2 = \bigl(4,8)$

b) $P_1 = \bigl(10,5)$ und $P_2 = \bigl(-2,-3)$

c) $P_1 = \bigl(4,8)$ und $P_2 = \bigl(-7,8)$

Die obigen Rechenschritte kann man auch in einer einzigen Formel zusammenfassen, um direkt aus zwei gegebenen Punkten die Gleichung der linearen Funktion zu bestimmen, ohne die Rechenschritte einzeln durchzuführen. Diese FOrmel nennt man auch die "Zwei-Punkte-Form" einer linearen Funktion.

Zwei-Punkte-Form einer linearen Funktion

Die "Zwei-Punkte-Form" einer linearen Funktion besitzt die Form: $f(x) = {y_2-y_1 \over x_2-x_1}*(x-x_1)+y_1$. Setzt man in diese Formel die Werte der beiden gegebenen Punkte ein, so erhält man direkt (nachdem die rechte Seite so weit wie möglich "vereinfacht" wurde) die fertige Gleichung der linearen Funktion.

Aufgabe:

Berechne die Gleichung der linearen Funktionen aus den Punkten von der Aufgabe von oben. Zur Kontrolle: Es müssen die gleichen Funktionsgleichungen herauskommen wie bei der obigen Aufgabe!

Bestimmung der Funktionsgleichung aus einem Punkt und der Steigung (Punkt-Steigungs-Form)

Die zweite Möglichkeit ist die Berechnung der Funktionsgleichung aus einen Punkt P welcher auf der Geraden der linearen Funktion liegt und die Steigung m. Um sich dies wieder ins Gedächtnis zu rufen bearbeite dazu die folgenden beiden Aufgaben.

Schaue dir das folgende Video an und bearbeite die folgenden Aufgaben.

1. Schaue es dir noch einmal an und notiere dir schriftlich was bei der Berechnung der Gleichung einer linearen Funktion gegeben und gesucht ist, sowie die zentralen Schritte und wichtigsten Formeln.
2. Vergleiche mit der Lösung.

Gegeben: Ein Punkt sowie die Steigung m Gesucht: b, sodass die Funktionsgleichung f(x)$=$m*x+b gefunden wird. Vorgehen: 1) Notiere die allgemeine Punkt-Steigungs-Form $f(x) = m*(x-x_1)+y_1$ 2) Setze m sowie die Koordinaten des gegebenen Punktes in die Formel ein.

3) "Vereinfache" die rechte Seite der Gleichung und schreibe die "fertige" Gleichung als Lösung auf.

Punkt-Steigungs-Form einer linearen Funktion

Die "Punkt-Steigungs-Form" einer linearen Funktion besitzt die Form: $f(x) = m*(x-x_1)+y_1$. Setzt man in diese Formel die Steigung m und die Koordinaten des Punktes ein, so erhält man direkt (nachdem die rechte Seite so weit wie möglich "vereinfacht" wurde) die fertige Gleichung der linearen Funktion.

Aufgabe: Berechne die Funktionsgleichung mit der Form f(x)$=$m*x+b aus den beiden gegebene Punkten schriftlich.

a) $P = \bigl(-7,1)$ und $m = 2$

b) $P = \bigl(0,5)$ und $m = -3$

c) $P = \bigl(2,2)$ und $m = 1$

Schnittpunkte mit den Koordinatenachsen

In diesem Abschnitt wiederholst du die Interkation einer linearen Funktion mit den beiden Koordinatenachsen des Koordinatensystems. Dazu betrachten wir zunächst den Schnittpunkt mit der x-Achse und im Anschluss den Schnittpunkt mit der y-Achse.

Schnittpunkt mit der x-Achse (Nullstelen)

Die Schnittpunkte einer Funktion mit der x-Achse nennt man auch Nullstellen, es sind also Stellen, an welchen der Funktionswert (y-Wert) den Wert 0 annimmt. Lineare Funktionen können entweder keine eine oder unendlich viele Nullstellen haben.

Beziehung zwischen Geraden

Zwei oder mehrere Geraden können zueinander in Beziehung stehen. Dabei sind lediglich die folgenden Fälle möglich:

a) Die Geraden schneiden sich

b) Die Geraden sind parallel

c) Die Geraden sind identisch

d) Die Geraden schneiden sich im rechten Winkel

Kennst du all diese Fälle noch und wie man sie am Graphen oder an der Funktionsgleichung erkennt?

Im folgenden ist ChatGPT in den Lernpfad eingebettet. Du hast damit die Möglichkeit deinem Wissenstand entsprechend zu wiederholen, indem du ChatGPT deine Fragen stellst und immer weiter nachfragst, wenn du etwas nicht richtig verstehst. Stell für die Fälle a) - d) Merksätze auf, die dir bei der Bearbeitung von Aufgaben helfen können. Notiere diese in deinem Heft.

Fühlst du dich fit genug, um Aufgaben zu bearbeiten?