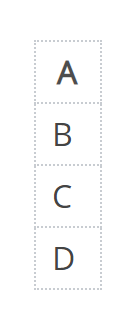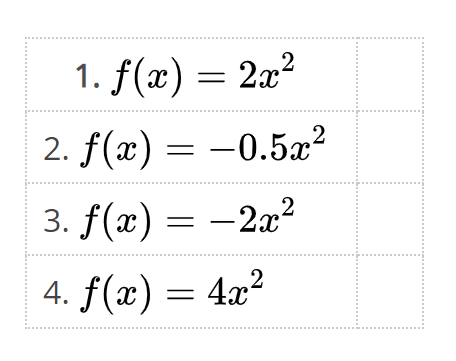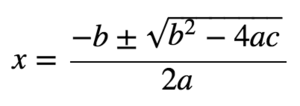Quadratische Funktionen - Was ist das?: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 9: | Zeile 9: | ||
}} | }} | ||
==Übersicht == | ==Übersicht== | ||
'''<big>Was dich im Laufe dieses Lernpfades erwarten wird:</big>''' | '''<big>Was dich im Laufe dieses Lernpfades erwarten wird:</big>''' | ||
<br /> | <br /> | ||
| Zeile 324: | Zeile 324: | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
{{Lösung versteckt|1=[[Datei:Lösung parameter 1.png|rahmenlos|500px|zentriert]]}}<br />{{Box | {{Lösung versteckt|1=[[Datei:Lösung parameter 1.png|rahmenlos|500px|zentriert]]}}<br />{{Box | ||
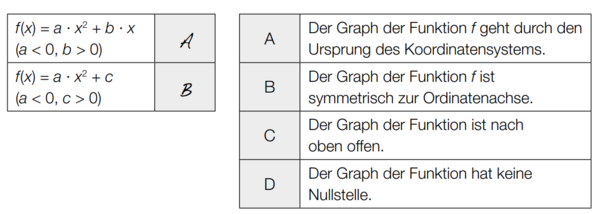
|1=Aufgabe | |1=Aufgabe 10 | ||
|2=Ordne den Funktionsgleichungen jeweils die zugehörige Bedingung aus A bis D zu. | |2=Ordne den Funktionsgleichungen jeweils die zugehörige Bedingung aus A bis D zu. | ||
| Zeile 342: | Zeile 342: | ||
{{Box | {{Box | ||
|1=Aufgabe | |1=Aufgabe 11 | ||
|2=Betrachte nun folgende Funktionsgraphen. | |2=Betrachte nun folgende Funktionsgraphen. | ||
| Zeile 420: | Zeile 420: | ||
<br />{{Box | <br />{{Box | ||
|1=Aufgabe | |1=Aufgabe 12 | ||
|2=Betrachte nun erneut die gleichen Funktionsgraphen aus Aufgabe 9. | |2=Betrachte nun erneut die gleichen Funktionsgraphen aus Aufgabe 9. | ||
| Zeile 442: | Zeile 442: | ||
Funktion C besitzt keine Nullstelle}}{{Box | Funktion C besitzt keine Nullstelle}}{{Box | ||
|1=Aufgabe | |1=Aufgabe 13 | ||
|2=Gegeben ist eine quadratische Funktion mit der Funktionsgleichung <math>f(x)=-4x^2-3x+1</math>. | |2=Gegeben ist eine quadratische Funktion mit der Funktionsgleichung <math>f(x)=-4x^2-3x+1</math>. | ||
| Zeile 463: | Zeile 463: | ||
<math>x_2 = 0.25 </math>}}{{Box | <math>x_2 = 0.25 </math>}}{{Box | ||
|1=Aufgabe | |1=Aufgabe 14 | ||
|2=Gegeben ist eine quadratische Funktion mit der Funktionsgleichung <math>f(x)=-x^2+2x+3</math>. | |2=Gegeben ist eine quadratische Funktion mit der Funktionsgleichung <math>f(x)=-x^2+2x+3</math>. | ||
| Zeile 515: | Zeile 515: | ||
=Anwendung quadratischer Funktionen= | =Anwendung quadratischer Funktionen= | ||
{{Box | {{Box | ||
|1=Aufgabe | |1=Aufgabe 15 | ||
|2=Der Graph der Funktion f beschreibt die Flugbahn einer Speerspitze bei einem bestimmten Wurf. | |2=Der Graph der Funktion f beschreibt die Flugbahn einer Speerspitze bei einem bestimmten Wurf. | ||
| Zeile 529: | Zeile 529: | ||
2) Berechne die horizontale Entfernung vom Abwurfpunkt, in der die Speerspitze bei diesem Wurf auf dem Boden auftrifft. | 2) Berechne die horizontale Entfernung vom Abwurfpunkt, in der die Speerspitze bei diesem Wurf auf dem Boden auftrifft. | ||
|3=Arbeitsmethode}}{{Box | |||
|1=Aufgabe | {{Lösung versteckt|1=1) Betrachte dazu den Schnittpunkt mit der y-Achse (Parameter c) |2=Hilfe anzeigen|3=Hilfe verbergen}} | ||
<br /> | |||
{{Lösung versteckt|1=2) Horizontale Entfernung = Nullstelle. |2=Hilfe anzeigen|3=Hilfe verbergen}} | |||
<br /> | |||
|3=Arbeitsmethode}}{{Lösung versteckt|1=1) Der Sperr wurde aus einer Höhe von 1.8m abgeworfen. | |||
f(0) = 1.8m | |||
Wir erhalten den Wert auch, indem wir x = 0 in die Funktionsgleichung einsetzen. | |||
<math>f(0)=-0.01*0^2+0.7*0+1.8 = 1.8</math> | |||
2) Horizontale Entfernung = Nullstelle | |||
<math>0=-0.01x^2+0.7x+1.8</math> | |||
abc Formel: | |||
<math>x = \frac{-b\pm\sqrt{b^2 -4ac}}{2a}</math> | |||
<math>x = \frac{-0.7\pm\sqrt{0.7^2 -4*-0.01*1.8}}{2*-0.01}</math> | |||
<math>x_1 = -2.5</math> | |||
<math>x_2 = 72.5 </math> | |||
Für die Interpretation kommt nur die positive Lösung <math>x_2 </math> in Frage: | |||
Der Sperr trifft also nach ca. 72.5 Meter auf dem Boden auf.}}<br />{{Box | |||
|1=Aufgabe 16 | |||
|2=Die Wurfbahn eines schräg nach oben geworfen Balles kann mit der Funkion: <math>h(x)=-0.2x^2+x+1.5</math> beschrieben werden. | |2=Die Wurfbahn eines schräg nach oben geworfen Balles kann mit der Funkion: <math>h(x)=-0.2x^2+x+1.5</math> beschrieben werden. | ||
x ist die horizontale Entfernung von der Abwurfstelle in Meter | x ist die horizontale Entfernung von der Abwurfstelle in Meter | ||
| Zeile 542: | Zeile 570: | ||
3) Bestimmt die Maximale Höhe, die der Ball erreicht. | 3) Bestimmt die Maximale Höhe, die der Ball erreicht. | ||
|3=Arbeitsmethode}}{{Box | |||
|1=Aufgabe | {{Lösung versteckt|1=1) Abschusshöhe |2=Hilfe anzeigen|3=Hilfe verbergen}} | ||
<br /> | |||
{{Lösung versteckt|1=2) waagrechte Entfernung = Nullstelle. |2=Hilfe anzeigen|3=Hilfe verbergen}} | |||
<br /> | |||
{{Lösung versteckt|1=1) Maximum = Scheitelpunkt |2=Hilfe anzeigen|3=Hilfe verbergen}} | |||
<br /> | |||
|3=Arbeitsmethode}}{{Lösung versteckt|1=1) h(0) gibt die Höhe nach 0 Metern an. Das bedeutet die Höhe beim Abschuss = Abschusshöhe. | |||
Diese entspricht dem Schnittpunkt mit der y-Achse. (Parameter c = 1.5) | |||
Wir erhalten den Wert auch, indem wir x = 0 in die Funktionsgleichung einsetzen. | |||
<math>h(0)=-0.2*0^2+0+1.5 = 1.5</math> | |||
2) Der Sperr wurde aus einer Höhe von 1.8m abgeworfen. | |||
f(0) = 1.8m | |||
2) Horizontale Entfernung = Nullstelle | |||
<math>0=-0.01x^2+0.7x+1.5</math> | |||
abc Formel: | |||
<math>x = \frac{-b\pm\sqrt{b^2 -4ac}}{2a}</math> | |||
<math>x = \frac{-1\pm\sqrt{1^2 -4*-0.2*1.5}}{2*-0.2}</math> | |||
<math>x_1 = -1.2</math> | |||
<math>x_2 = 6.2 </math> | |||
Für die Interpretation kommt nur die positive Lösung <math>x_2 </math> in Frage: | |||
Der Ball trifft also nach ca. 6.2 Meter auf dem Boden auf. | |||
3) Die maximale Höhe kann durch den Scheitelpunkt ermittelt werden. | |||
<math>S = \Bigl(\frac{-b}{2a}|\frac{-4ac-b^2}{4a} | |||
\Biggr)</math>}}{{Box | |||
|1=Aufgabe 17 | |||
|2=Im Computerspiel Angry Birds muss man mithilfe einer Schleuder grüne Schweine treffen. Als Wurfgeschoße stehen verschiedene Vögel zur Verfügung. | |2=Im Computerspiel Angry Birds muss man mithilfe einer Schleuder grüne Schweine treffen. Als Wurfgeschoße stehen verschiedene Vögel zur Verfügung. | ||
| Zeile 554: | Zeile 619: | ||
1) Bestimme die Funktionsgleichung f(x) die "Red"s Flugbahn beschreibt, damit er das Schwein trifft. | 1) Bestimme die Funktionsgleichung f(x) die "Red"s Flugbahn beschreibt, damit er das Schwein trifft. | ||
|3=Arbeitsmethode}}{{Box | |3=Arbeitsmethode}}{{Box | ||
|1=Aufgabe | |1=Aufgabe 18 | ||
|2=Eine einspurige Tordurchfahrt hat die Höhe 5 m und die Bodenbreite 6m. Der Torbogen lässt sich durch eine quadratische Funktion f der Form <math>h(x)=ax^2+c</math> beschreiben, wenn der Ursprung im Fußpunkt der größten Höhe gewählt wird. | |2=Eine einspurige Tordurchfahrt hat die Höhe 5 m und die Bodenbreite 6m. Der Torbogen lässt sich durch eine quadratische Funktion f der Form <math>h(x)=ax^2+c</math> beschreiben, wenn der Ursprung im Fußpunkt der größten Höhe gewählt wird. | ||
Version vom 4. April 2023, 17:52 Uhr
Quadratische Funktionen - was ist das?
Bisher hast du bereits gelernt, was Funktionen sind und dabei besonders die Linearen Funktionen unter die Lupe genommen. In diesem Lernpfad geht es nun darum Eigenschaften einer weiteren Art von Funktionen zu entdecken. Du hast hier die Möglichkeit, dir selbstständig Wissen über Quadratische Funktionen anzueignen.
Übersicht
Was dich im Laufe dieses Lernpfades erwarten wird:
- Quadratische Funktionen im Alltag
- Quadratische Funktionen kennenlernen
- Die Parameter a und c
- Nullstellen Quadratischer Funktionen
- Anwendung Quadratischer Funktionen
Bevor es losgeht:
Bevor du mit der Bearbeitung des Lernpfades starten kannst, erfährst du hier noch einige Informationen, die dabei Helfen die Übersicht zu bewahren. Außerdem erfährst du welche Lernziele du durch den Lernpfad erreichen wirst.
Infos für die Bearbeitung
Damit du dich in dem Lernpfad leicht zurechtfindest, sind auf dieser Seite einige Informationen zusammengestellt.
Oben auf dem Bildschirm im Inhaltsverzeichnis siehst du eine Aufzählung der Kapitel, die du durchlaufen wirst. Du kannst durch einfaches Anklicken zwischen den Kapiteln hin- und herspringen.
Im Lernpfad triffst du auf folgende Bausteine:
Hier sollst du aktiv werden und selbstständig Neues entdecken.
Neben klassischen Aufgaben, die du in deinem Heft mit Papier und Stift bearbeiten sollst, können Aufgaben auch in Form interaktiver Applets auftreten. Von Kreuzworträtseln über GeoGebra-Applets und Zuordnungsaufgaben wird dir hier eine große Spannbreite begegnen. Genauere Erklärungen stehen bei der jeweiligen Aufgabe.Bei einigen Aufgaben stehen dir außerdem Hilfen und Tipps zur Verfügung, wenn du nicht weiter kommst. Versuche immer zuerst die Lösung alleine herauszufinden, dann kannst du dir die Tipps anschauen. Diese bekommst du durch das Anklicken von:
Wenn du eine Aufgabe gelöst hast, bekommst du sofort eine Rückmeldung, ob dein Ergebnis richtig ist oder nicht. Dies geschieht entweder durch einen entsprechenden Lösungs-Button innerhalb interaktiver Applets oder durch Anklicken von:
Lernziele
Das wirst du lernen:
- Quadratische Funktionen in Wertetabellen, als Graphen und in Termen darstellen und erkennen
- Auswirkungen der Parameter a und c in einem quadratischen Funktionsterm auf den zugehörigen Graphen erkennen und beschreiben
- Graphen quadratischer Funktionen als Parabeln identifizieren und interpretieren
- Nullstellen quadratischer Funktionen berechnen
- Quadratische Funktionsterme interpretieren und mit ihnen rechnen
Ein letzter Hinweis bevor es losgeht!
Du kannst dir die Zeit bei der Bearbeitung der einzelnen Kapitel des Lernpfades selber einteilen. Das heißt einerseits, dass du alle neuen Entdeckungen und Übungen in deinem Tempo durchlaufen kannst, andererseits musst du aber auch selbstständig darauf achten, nicht unnötig zu trödeln und voranzukommen.
Nun kann es losgehen!
Quadratische Funktionen im Alltag
Um uns quadratische Funktionen leichter vorstellen zu können betrachten wir zunächst einige Beispiele, wo quadratische Funktionen im realen Leben vorkommen. So kannst du im Alltag oder auf einem Städtetrip immer wieder bogenförmige Bauwerke und Brücken entdecken. Ich bin mir sicher, dass so derartige Bauwerke auch in deiner Stadt finden kannst.
Auch in der Natur kommen solche Bögen immer wieder vor, so zum Beispiel bei Bergmassiven.
Hier sind einige Beispiele von quadratischen Funktionen, wie sie im im echten Leben auftreten.Aber nicht nur bei Bauwerken oder in der Natur kommen quadratische Funktionen häufig vor. Auch bei vielen Sportarten, sind wir unbewusst mit quadratischen Funktionen konfrontiert.
Ob beim Basketball- oder Fußball spielen ist es möglich vergleichbare Bögen zu entdecken. Achte einmal darauf, wie ein abgeworfener oder abgeschossener Ball durch die Luft fliegt.
Bei dieser Aufgabe sollst du nun selbst eine Quadratische Funktion in deiner Umgebung finden.
a) Suche dazu parabelförmige Bögen in deiner Umgebung. Du kannst bei dir Zuhause suchen oder auch im Park oder in der Stadt suchen. Fotografiere mindestens eine Parabel und notiere dir, wo du sie entdeckt hast und wie sie aussieht (z. B. breit, schmal, nach oben oder nach unten geöffnet).
b) Bring dein Foto in der nächsten Stunde mit und vergleiche sie mit einem Partner. Berichte deinem Partner von deinen Entdeckungen. Sammelt die Orte, Bilder und Beschreibungen in euren Schulübungsheftern.
Quadratische Funktionen kennenlernen
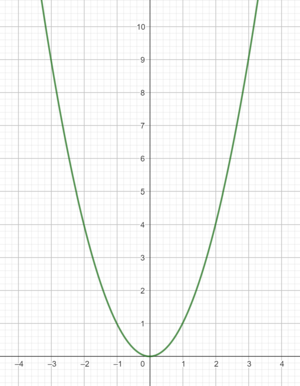
Nachdem wir nun eine bessere Vorstellung darüber haben, wie quadratische Funktionen aussehen können und wo sie auch im Alltag vorkommen, betrachten wir nun die zunächst die einfachste quadratische Funktion mit der Funktionsgleichung .
Für diese Aufgabe benötigst du dein Schulübungsheft.
a) Übernimm die Werte aus der dargestellten Wertetabelle in dein Heft und ergänze sie um weitere Werte, die dir helfen den passenden Graphen in ein Koordinatensystem einzuzeichnen.
b) Zeichne den zugehörigen Graphen in ein Koordinatensystem.
| x | y = f(x) |
|---|---|
| -3 | 9 |
| -2 | 4 |
| 1 | 1 |
| 0 | 0 |
| 1 | |
| 2 | |
| 3 |
Wenn du dir nicht mehr sicher bist, wie du eine Wertetabelle erstellst oder Hilfe beim Einzeichnen in das Koordinatensystem benötigst, kannst du dir dieses Video bis Minute 4 anschauen:
Den Graph dieser quadratischen Funktion nennt man Normalparabel.
Die Normalparabel hat ihren tiefsten Punkt an der Stelle . Dieser Punkt wird Scheitelpunkt genannt.
Die Parabel der Form hat noch zweit weitere besondere Eigenschaften:
- Die Parabel ist nach oben geöffnet.
- Die Parabel ist symmetrisch zur y-Achse.
Wenn du dir die Bilder vom Beginn des Lernpfades noch einmal anschaust, dann fällt auf, dass die abgebildeten Parabeln alle anders aussehen als die gerade kennengelernte Normalparabel. In der Natur und in Anwendungen wird der Funktionsterm der Normalparabel (f(x) = x2) variiert und es entstehen die unterschiedlichsten Parabeln.
Die Normalparabel kann also gestreckt, gestaucht oder auch gespiegelt werden, wodurch sie eine andere Form annimmt.
Um herauszufinden, wie genau sich die bereits kennengelernte Normalparabel der Form verändern kann bist nun du wieder an der Reihe!
Die Parameter a und c
Für diese Aufgabe benötigst du dein Schulübungsheft.
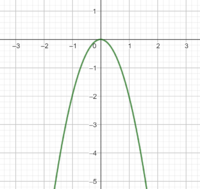
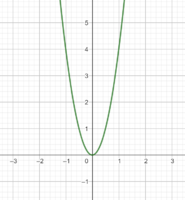
Wie verändert sich der Graph, wenn man statt der Funktion folgende Funktionen gegeben hat:
- (1) , (2) und (3) ?
a) Notiere Vermutungen darüber, wie die Graphen der Funktionen (1), (2) und (3) aussehen könnten (ohne diese zu zeichnen!).
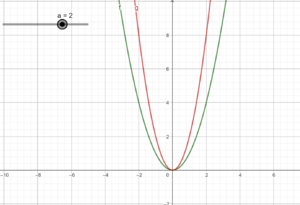
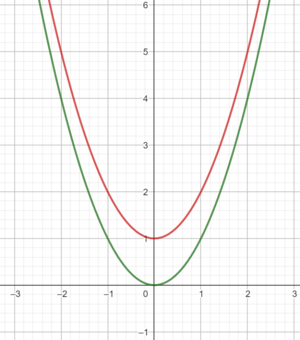
In dem Applet ist die Normalparabel die du bereits kennengelernt hast grün eingezeichnet. Du kannst mit dem Schieberegler verschiedene Werte für "" eingeben. Dadurch wird der rote Graph verändert.
Klicke auf folgenden Link um zum Geogebra Applet zu gelangen:
https://www.geogebra.org/m/fwjxkegk
Richtige Vermutungen können wie folgt lauten:
1. Die Parabel von Funktion (1) ist im Vergleich zu der Normalparabel schmaler, da die quadrierten x-Werte () durch den Vorfaktor 2 immer verdoppelt werden. Der zugehörige y-Wert wird dadurch größer.
2. Die Parabel von Funktion (2) ist im Vergleich zu der Normalparabel breiter, da die quadrierten x-Werte () durch den Vorfaktor 1/2 immer halbiert werden. Der zugehörige y-Wert wird dadurch kleiner.
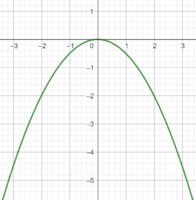
3. Die Parabel von Funktion (3) ist im Vergleich zu der Normalparabel "umgedreht", da die quadrierten x-Werte () durch den Vorfaktor -1 immer negative Werte annehmen. Der y-Wert ist also immer negativ.
In dem folgenden Lückentext werden die Erkenntnisse, die du aus Aufgabe 1 mitnehmen konntest, noch einmal ausformuliert. Füge die fehlenden Begriffe und Zahlen in die Lücken.
Wenn a kleiner Null ist (), dann ist die Parabel nach unten geöffnet.
Wenn a größer Null ist (), dann ist die Parabel nach oben geöffnet.
Wenn a zwischen minus Eins und Eins liegt (), dann wird der Graph der Funktion breiter. Man nennt das auch eine gestauchte Parabel.
Wenn a kleiner als minus Eins () oder größer als Eins ist (), dann wird der Graph der Funktion gestreckt. Er ist somit schmaler als die Normalparabel.
Multipliziert man mit einem Faktor a, wird die Parabel gestreckt, gestaucht und/oder gespiegelt. Für (mit a ≠ 0) gilt demnach:
a > 0: Die Parabel ist nach oben geöffnet.
a < 0: Die Parabel ist nach unten geöffnet.
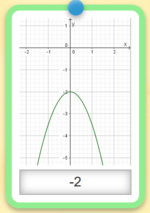
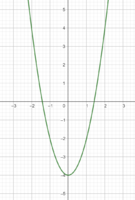
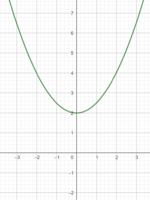
Knobelaufgabe
Tipp: Wenn du die Kärtchen mit den Graphen anklickst, werden sie dir vergrößert angezeigt.
Nun hast du bereits herausgefunden, wie sich eine Quadratische Funktion der Form durch Multiplikation mit dem Parameter a verändern lässt.
Die Quadratische Funktion kann zudem durch den Parameter c verändert werden. Inwiefern der Parameter c die Normalparabel verändert, wirst du durch die nächste Aufgabe selbst herausfinden.
Für diese Aufgabe benötigst du dein Schulübungsheft.
Wie verändert sich der Graph, wenn man statt der Funktion folgende Funktionen gegeben hat:
- (1) , (2) ?
a) Notiere Vermutungen darüber, wie die Graphen der Funktionen (1) und (2) aussehen könnten. Skizziere die Funktionsgraphen dazu in ein passendes Kooridinatensystem.
In dem Applet ist die Normalparabel die du bereits kennengelernt hast grün eingezeichnet. Du kannst mit dem Schieberegler verschiedene Werte für "" eingeben. Dadurch wird der rote Graph verändert.
Klicke auf folgenden Link um zum Geogebra Applet zu gelangen:
https://www.geogebra.org/m/dzeed7zm
Richtige Vermutungen können wie folgt lauten:
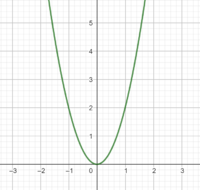
1. Die Parabel von Funktion (1) ist im Vergleich zu der Normalparabel nach oben verschoben, da die x-Werte nach dem quadrieren mit 3 addiert werden.
2. Die Parabel von Funktion (2) ist im Vergleich zu der Normalparabel nach unten verschoben, da die x-Werte nach dem quadrieren mit 2 subtrahiert werden.
Addiert oder subtrahiert man eine Zahl c von , wird die Parabel entlang der y-Achse verschoben. Für gilt:
c > 0: Die Parabel wird entlang der y-Achse nach oben verschoben.
c < 0: Die Parabel wird entlang der y-Achse nach unten verschoben.
Nun versuchen wir die Auswirkungen der beiden Parameter a und c zu verbinden.
Für diese Aufgabe benötigst du dein Schulübungsheft.
Zeichne folgende quadratische Funktionen in geeignete Koordinatensysteme.
- (1) , (2) und (3) ?
Wir haben die Parameter a und c genauer untersucht, und herausgefunden wie sie die Quadratische Funktion verändern. Um zur allgemeinen Funktionsgleichung zu gelangen, fehlt uns noch der Parameter b. Welchen Einfluss dieser auf den Graphen einer quadratischen Funktion hat, kannst du erneut in folgender Geogebra Datei selbst erkunden.
Klicke auf folgenden Link um zum Geogebra Applet zu gelangen:
https://www.geogebra.org/m/svmwzgzg
Die auf dieser Seite gewonnen Erkenntnisse können kombiniert werden und ergeben quadratische Funktion der Form . Diese Form heißt Normalform.
Zur Berechnung der nächsten Aufgaben werden wir stets diese Form verwenden.
Wir haben zu Beginn dieses Lernpfads bereits den Begriff des Scheitelpunktes kennengelernt. Wir können nun nicht nur von der Normalparabel, sondern von jeder beliebigen quadratischen Funktion den Scheitelpunkt bestimmen.
1)
Scheitelpunkt A = (2|- 4)
Scheitelpunkt B = (2|1)
Scheitelpunkt C = (- 2|- 2)
2)
Ob eine Funktion einen Hoch- oder Tiefpunkt besitzt, hängt vom Parameter a ab.
Wenn a > 0 ist die Parabel nach oben offen. Dadurch hat die Funktion einen Tiefpunkt als Scheitelpunkt.
Wenn a < 0 ist die Parabel nach unten offen. Dadurch hat die Funktion einen Hochpunkt als Scheitelpunkt.Der Scheitelpunkt ist abhängig vom Parameter a entweder ein Hoch- oder Tiefpunkt.
Den Scheitelpunkt kann man nicht nur vom Funktionsgraphen anlesen. Mann kann ihn auch mit folgender Formel berechnen.
Nullstellen
Nachdem wir nun eine genauere Vorstellung von quadratischen Funktionen der Form haben, können wir uns nun dem Rechnen mit quadratischen Funktionen widmen.
Wie du möglicherweise bereits aus den bisher betrachteten Parabeln erkennen konntest, gibt es quadratische Funktionen, welche die x Achse keinmal, einmal oder sogar 2 mal schneiden.
Diese Schnittpunkte mit der x-Achse nennt man Nullstellen. An diesen Nullstellen hat die Funktion den Funktionswert y = 0.
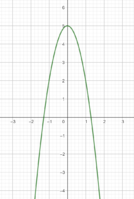
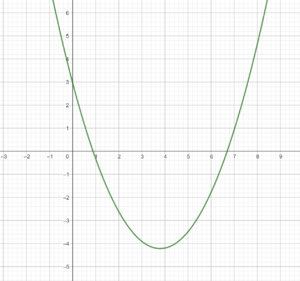
Du kannst die Nullstellen also aus den jeweiligen Funktionsgraphen ablesen. So sehen wir, dass die erste Funktion keine Nullstellen besitzt und die dritte Funktion genau eine Nullstelle an der Stelle x = 0 besitzt.
Anhand der Grafik der zweiten Funktion können wir zwar ablesen, dass diese zwei Nullstellen besitzt. Den genauen Wert können wir durch das Ablesen hier allerdings nicht genau bestimmen.
Daher benötigen wir eine Möglichkeit zur genauen Berechnung von Nullstellen.
Zur Berechnung dieser Nullstellen benötigst du quadratische Gleichungen. Wir setzen den y-Wert dazu 0.
Nun können wir mit der bereits bekannten a,b,c Formel die Nullstellen der quadratischen Funktion berechnen.
Ausschlaggebend für die Anzahl der Lösungen einer quadratischen Gleichung und damit für die Nullstellen einer quadratischen Funktion ist der Ausdruck unter der Wurzel, die Diskriminante.
- 2 Nullstellen: Unter der Wurzel steht eine positive Zahl.
- 1 Nullstelle: Unter der Wurzel steht 0.
- Keine Nullstelle: Unter der Wurzel steht eine negative Zahl.
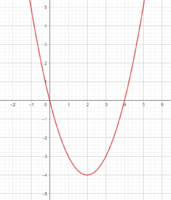
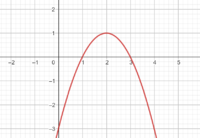
Funktion A besitzt 2 Nullstellen: x1 = 0 x2 = 4
Funktion B besitzt 2 Nullstellen: x1 = 1 x2 = 3
Funktion C besitzt keine NullstelleGegeben ist eine quadratische Funktion mit der Funktionsgleichung .
Gegeben ist eine quadratische Funktion mit der Funktionsgleichung .
1) Die Funktion f ist der Form . Gib a, b und c an!
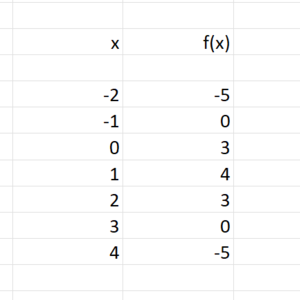
2) Erstelle eine Wertetabelle und zeichne den Graphen von f.
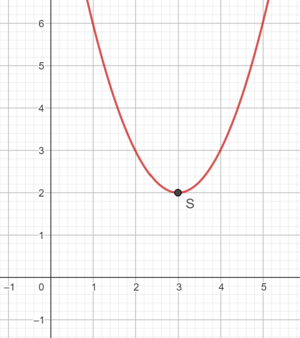
3) Ermittle den Scheitelpunkt der Funktion.
4) Lese die Nullstellen aus dem Funktionsgraphen ab.
5) Ermittle die Nullstellen rechnerisch und vergleiche sie mit deinen abgelesenen Werten.
1)
a = - 1
b = 2
c = 3
2)
3) Scheitelpunkt S = (1|4)
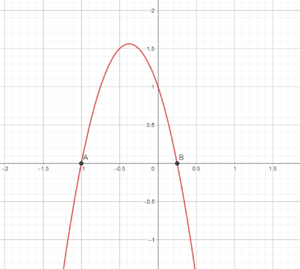
4) Die Funktion besitzt 2 Nullstellen. x1 = -1 und x2 = 3.
5) Rechnerisch mithilfe der abc Formel:
Anwendung quadratischer Funktionen
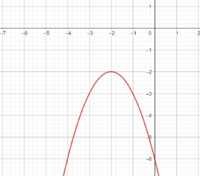
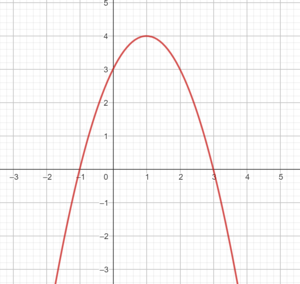
Der Graph der Funktion f beschreibt die Flugbahn einer Speerspitze bei einem bestimmten Wurf.
x ... horizontale Entfernung vom Abwurfpunkt in m
f(x) ... Höhe über dem Boden bei der horizontalen Entfernung x in m
1) Gib an, aus wie vielen m Höhe der Speer abgeschossen wurde.
2) Berechne die horizontale Entfernung vom Abwurfpunkt, in der die Speerspitze bei diesem Wurf auf dem Boden auftrifft.
1) Der Sperr wurde aus einer Höhe von 1.8m abgeworfen. f(0) = 1.8m
Wir erhalten den Wert auch, indem wir x = 0 in die Funktionsgleichung einsetzen.
2) Horizontale Entfernung = Nullstelle
abc Formel:
Für die Interpretation kommt nur die positive Lösung in Frage:
Der Sperr trifft also nach ca. 72.5 Meter auf dem Boden auf.Die Wurfbahn eines schräg nach oben geworfen Balles kann mit der Funkion: beschrieben werden. x ist die horizontale Entfernung von der Abwurfstelle in Meter h(x) ist die Höhe des Balles in Meter über dem waagrechten Boden.
1) Bestimme und interpretiere h(0).
2) Berechne in welcher waagrechten Entfernung von der Abwurfstelle der Ball wieder auf den Boden auftritt.
3) Bestimmt die Maximale Höhe, die der Ball erreicht.
1) h(0) gibt die Höhe nach 0 Metern an. Das bedeutet die Höhe beim Abschuss = Abschusshöhe. Diese entspricht dem Schnittpunkt mit der y-Achse. (Parameter c = 1.5) Wir erhalten den Wert auch, indem wir x = 0 in die Funktionsgleichung einsetzen.
2) Der Sperr wurde aus einer Höhe von 1.8m abgeworfen.
f(0) = 1.8m
2) Horizontale Entfernung = Nullstelle
abc Formel:
Für die Interpretation kommt nur die positive Lösung in Frage:
Der Ball trifft also nach ca. 6.2 Meter auf dem Boden auf.
3) Die maximale Höhe kann durch den Scheitelpunkt ermittelt werden.
Im Computerspiel Angry Birds muss man mithilfe einer Schleuder grüne Schweine treffen. Als Wurfgeschoße stehen verschiedene Vögel zur Verfügung.
Der Vogel "Red" sitzt auf seiner Schleuder, 0.5m über dem Boden. Das zu treffende Schwein sitzt im Punkt (11|1.5). Außerdem weiß man, dass "Red" seinen höchste Höhe von 4 m nach 6m erreicht.
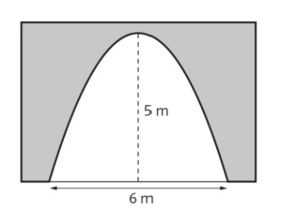
1) Bestimme die Funktionsgleichung f(x) die "Red"s Flugbahn beschreibt, damit er das Schwein trifft.Eine einspurige Tordurchfahrt hat die Höhe 5 m und die Bodenbreite 6m. Der Torbogen lässt sich durch eine quadratische Funktion f der Form beschreiben, wenn der Ursprung im Fußpunkt der größten Höhe gewählt wird.
In der EU dürfen Lastwägen höchstens 4 m hoch und höchstens 2,55 breit sein. Kann jeder Lastwagen, der diese Vorschriften erfüllt, die Tordurchfahrt passieren?