Verhalten an den Definitionslücken

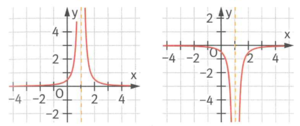
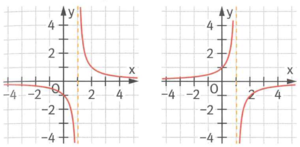
Eine Definitionslücke $x_p$ der Funktion, für die der Nenner, aber nicht Zähler null wird, ist eine Polstelle. Hier hat der Graph der Funktion eine senkrechte Asymptote mit der Gleichung $x=x_p$

Es gilt: $\textstyle \lim_{x \to x_p} \displaystyle f(x) = \pm\infty$

Tipp: Faktorsiere den Nenner bevor die die Grenzwertbetrachtung durchführst.

Hierbei unterscheidet man zwischen Polstellen gerader Ordnung, also mit VZW

und ungerader Ordnung, also ohne VZW

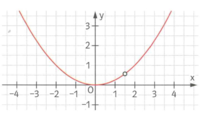
Ist eine Definitionslücke auch gleichzeitig die Nullstelle der Zählers, ist es eine hebbare Definitionslücke.

Es gilt: $\textstyle \lim_{x \to x_p} \displaystyle f(x) = a$

Es bietet sich hier an, die Symmetrie des Graphen auszunutzen.

zurück

Verhalten im Unendlichen

zurück zur Übersicht