Modellieren digital/Spielplatz: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 10: | Zeile 10: | ||
|Arbeitsmethode | |Arbeitsmethode | ||
}} | }} | ||
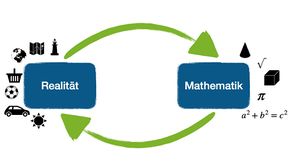
{{Box|Merke|Die Aufgabe Spielplatz, welche auch eine Modellierungsaufgabe ist, zeigt, dass man mit Hilfe von Mathematik Probleme aus der Realität lösen kann. Deshalb erfordern Modellierungsaufgaben auch immer, dass du ein Problem aus der Realität in die Mathematik übersetzt, indem du zum Beispiel eine passende Formel oder Konstruktion suchst. Das Ergebnis musst du dann am Ende wieder zurück in die Realität übersetzen, indem du es auf die Frage beziehst, interpretierst und dich fragst, ob das Ergebnis realistisch ist. | |||
[[Datei:Uebersetzungsprozesse Modellieren.jpg|zentriert|mini]] | |||
|Merksatz | |||
}} | |||
Du bist jetzt einer von Münsters Stadträten: Mache einen Vorschlag, wo der Spielplatz am besten gebaut werden sollte, indem du den gesuchten Ort in GeoGebra mathematisch modellierst und den Punkt S dort positionierst. | |||
<ggb_applet id="a2kpjxw2" width="600" height="500" border="888888" /> | |||
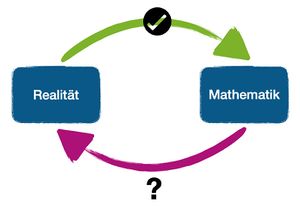
{{Box|Merke|Du konntest oben mithilfe von GeoGebra innerhalb der Mathematik ein Ergebnis für die Spielplatzaufgabe suchen. Dieses Ergebnis musst du nun wieder zurück in die Realität übersetzen, indem du es nutzt, um die Frage zu beantworten. | |||
Im Anschluss solltest du dich außerdem fragen, ob das Ergebnis realistisch ist. Dabei kannst du dich zum einen fragen, ob die gewählte mathematische Vorgehensweise sinnvoll war und zum anderen, ob das Ergebnis so in der Realität verwendbar ist, oder ob du zum Beispiel etwas über Parks weißt, das gegen deine Lösung spricht. | |||
[[Datei:UebersetzungsprozessMathematikRealität.jpg|zentriert|mini]] | |||
|Merksatz | |||
}} | |||
[[Datei:Notepad-117597.svg|links|43x43px]] Bearbeite in deinem Hefter folgende Aufträge: | |||
*Benenne, wo der Spielplatz gebaut werden sollte! | |||
*Beschreibe dein Vorgehen in GeoGebra! | |||
{{Lösung versteckt| | |||
Es soll ein Spielplatz gebaut werden, der möglichst nah an allen vier eingezeichneten Eingängen liegt. Es soll also ein Ort gefunden werden, der möglichst zu allen Eingängen den gleichen Abstand hat, damit man , egal von wo man den Park betritt, immer gleich weit zum Spielplatz laufen muss. Es wird also der Mittelpunkt eines Kreises durch alle vier Punkte gesucht. Der Park wird als eben angenommen und umfasst auch eine Wasserfläche. Als kürzeste Entfernung wird die Luftlinie betrachtet. <br \> | |||
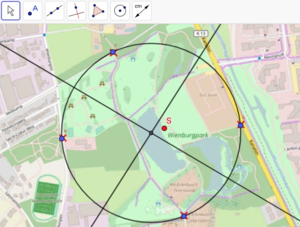
[[Datei:SpielplatzLoesung.png|links|mini]] So könnte ein Ausschnitt des GeoGebra-Applets aussehen. Der Ort, der von allen Eingängen gleich weit entfernt ist, ist der Mittelpunkt eines Kreises durch die vier Eingänge. <br \> | |||
Der ideale Bauort des Spielplatzes ist der konstruierte Schnittpunkt in der Abbildung, da dieser Punkt von allen Eingängen gleich weit entfernt liegt. <br \> | |||
Der konstruierte Punkt ist zwar mathematisch gesehen optimal, jedoch liegt er genau in dem eingezeichneten See. Da es wahrscheinlich nicht sinnvoll ist, eine Insel oder etwas Ähnliches im See zu errichten, sollte ein anderer Standort gewählt werden. Dazu könnte die Anbindung an die Wege betrachtet werden (optimaler Standort ist der, bei dem man vom Eingang etwa den gleichen Fußweg zum Spielplatz zurücklegen muss) oder die Lage anderer Ortspunkte (etwa des Sportplatzes) berücksichtigt werden. <br \> | |||
|Mögliche Lösung anzeigen|Mögliche Lösung verbergen}} | |||
{{Fortsetzung|weiter=Aufgabe 4: Torschuss|weiterlink=Modellieren digital/Torschuss}} | |||
Erstellt von: [[Benutzer:LFrenken|Lena Frenken]] ([[Benutzer Diskussion:LFrenken|Diskussion]]) | |||
[[Kategorie:Modellieren]] | |||
[[Kategorie:Geometrie]] | |||
[[Kategorie:GeoGebra]] | |||
Version vom 17. Juli 2022, 09:11 Uhr
Liebe Stadträte!
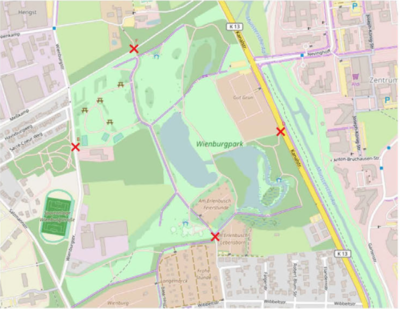
Dieses Jahr soll in den Wienburg-Park im Norden von Münster ein neuer Spielplatz gebaut werden. Unten seht ihr eine Karte des Parks abgebildet. In der Karte markiert sind die vier Eingänge des Parks. Nur an diesen vier Stellen kann man den Park betreten und wieder verlassen. Uns als Stadtrat ist es wichtig, dass keine Familie benachteiligt wird, egal an welchem Eingang sie den Park betritt. Heute wollen wir die Frage klären:
Wo sollte der Spielplatz gebaut werden?
Die Aufgabe Spielplatz, welche auch eine Modellierungsaufgabe ist, zeigt, dass man mit Hilfe von Mathematik Probleme aus der Realität lösen kann. Deshalb erfordern Modellierungsaufgaben auch immer, dass du ein Problem aus der Realität in die Mathematik übersetzt, indem du zum Beispiel eine passende Formel oder Konstruktion suchst. Das Ergebnis musst du dann am Ende wieder zurück in die Realität übersetzen, indem du es auf die Frage beziehst, interpretierst und dich fragst, ob das Ergebnis realistisch ist.
Du bist jetzt einer von Münsters Stadträten: Mache einen Vorschlag, wo der Spielplatz am besten gebaut werden sollte, indem du den gesuchten Ort in GeoGebra mathematisch modellierst und den Punkt S dort positionierst.

Du konntest oben mithilfe von GeoGebra innerhalb der Mathematik ein Ergebnis für die Spielplatzaufgabe suchen. Dieses Ergebnis musst du nun wieder zurück in die Realität übersetzen, indem du es nutzt, um die Frage zu beantworten.
Im Anschluss solltest du dich außerdem fragen, ob das Ergebnis realistisch ist. Dabei kannst du dich zum einen fragen, ob die gewählte mathematische Vorgehensweise sinnvoll war und zum anderen, ob das Ergebnis so in der Realität verwendbar ist, oder ob du zum Beispiel etwas über Parks weißt, das gegen deine Lösung spricht.
Bearbeite in deinem Hefter folgende Aufträge:
- Benenne, wo der Spielplatz gebaut werden sollte!
- Beschreibe dein Vorgehen in GeoGebra!
Es soll ein Spielplatz gebaut werden, der möglichst nah an allen vier eingezeichneten Eingängen liegt. Es soll also ein Ort gefunden werden, der möglichst zu allen Eingängen den gleichen Abstand hat, damit man , egal von wo man den Park betritt, immer gleich weit zum Spielplatz laufen muss. Es wird also der Mittelpunkt eines Kreises durch alle vier Punkte gesucht. Der Park wird als eben angenommen und umfasst auch eine Wasserfläche. Als kürzeste Entfernung wird die Luftlinie betrachtet.
Der ideale Bauort des Spielplatzes ist der konstruierte Schnittpunkt in der Abbildung, da dieser Punkt von allen Eingängen gleich weit entfernt liegt.
Der konstruierte Punkt ist zwar mathematisch gesehen optimal, jedoch liegt er genau in dem eingezeichneten See. Da es wahrscheinlich nicht sinnvoll ist, eine Insel oder etwas Ähnliches im See zu errichten, sollte ein anderer Standort gewählt werden. Dazu könnte die Anbindung an die Wege betrachtet werden (optimaler Standort ist der, bei dem man vom Eingang etwa den gleichen Fußweg zum Spielplatz zurücklegen muss) oder die Lage anderer Ortspunkte (etwa des Sportplatzes) berücksichtigt werden.
Erstellt von: Lena Frenken (Diskussion)