Lernpfad 8a - Volumina und Flächen/Cavalieri

Zur Person

Bonaventura Francesco Cavalieri (1598-1647) war ein
italienischer Mathematiker und Astronom.
Im "Satz von Cavalieri" (auch "Prinzip von Cavalieri" genannt)
geht es um die Volumengleichheit zweier Körper.

Erarbeitung des Satzes von Cavalieri

Peter: "Gib mir das rechte Glas, da passt mehr rein! Ich hab so einen Durst!"

Sandra: "So ein Quatsch! In die Gläser passt doch gleich viel!"

Wer hat nun Recht?

Um diese Frage zu beantworten, musst du wissen, welche Kriterien zwei Körper erfüllen müssen, damit sie das gleiche Volumen besitzen!

Arbeite diese Kriterien mit Hilfe der folgenden beiden Geogebra-Applets heraus und notiere deine Beobachtungen bzgl. der Volumina in deinem Heft unter der Überschrift "Der Satz von Cavalieri"

Zusätzliches Anschauungsmaterial zum Anfassen:

Wenn es dir schwer fällt, dir das Ganze richtig vorzustellen, nimm dir vorne am Pult zwei der Bierdeckelstapel und stelle die einzelnen Situationen damit nach.

Volumenvergleich von Zylindern 1

• Ziehe an dem grünen Punkt, um den Grundflächeninhalt des zweiten Zylinders zu verändern.
• Ziehe an dem roten Punkt, um die Höhe des dritten Zylinders zu verändern.

Volumenvergleich von Zylindern 2

• Welche der Zylinder besitzen das gleiche Volumen? Begründe deine Antwort! Nutze dazu die beweglichen Elemente!

Zurück zur Ausgangsfrage:Wer hat nun Recht? Peter oder Sandra? Begründe deine Antwort!

Verallgemeinerung der Erkenntnisse

Es ist relativ leicht nachzuvollziehen, dass die Kriterien, die du für die Volumengleichheit von Zylindern herausgearbeitet hast, auch für andere volumengleiche Körper (z.B. Prismen) gelten müssen.
Fasse deine gewonnenen Erkenntnisse zusammen und formuliere eine allgemeine Regel: Zwei Körper haben das gleiche Volumen, wenn für sie gilt ...

Du hast gerade Sachverhalte herausgearbeitet, welche Bonaventura Cavalieri in seinem berühmten (grundlegenden) Satz formuliert hat: Zwei Körper besitzen dasselbe Volumen, wenn alle ihre Schnittflächen in Ebenen parallel zu einer Grundebene in gleichen Höhen den gleichen Flächeninhalt haben.

Was ist bei unterschiedlichen Grundflächen?

Bisher haben wir nur Zylinder in Bezug auf ihr Volumen miteinander verglichen. Jeder Zylinder hat die gleiche Grundflächenform - einen Kreis.

Gilt der Satz von Cavalieri auch für Körper mit unterschiedlicher Grundflächenform? Untersuche dies mit Hilfe des folgenden Geogebra-Applets und begründe deine Antwort!

Volumenvergleich von Prismen mit unterschiedlicher Grundflächenform

• Nutze die beweglichen Elemente!
• Durch Ziehen an dem orangenen Punkt kannst du auch das dreiseitige gerade Prisma in ein dreiseitiges schiefes Prisma überführen.

Es kommt nicht auf die Form der Grundfläche, sondern auf den Grundflächeninhalt an!

Bsp.: Ein Prisma mit quadratischer Grundflächen und ein Prisma mit dreieckiger Grundfläche haben das gleiche Volumen, wenn ihre Grundflächeninhalte, ihre Höhe und die zur Grundfläche parallelen Schnittflächen in gleicher Höhe gleich groß sind.

Übungsaufgaben

Aufgabe

Berechne die Volumina der beiden Körper und gib das Ergebnis in Kubikdezimeter an!

a)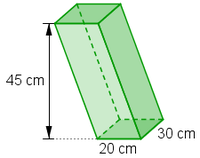 b)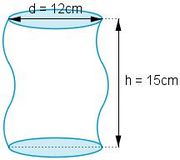

Das schiefe Prisma besitzt das gleiche Volumen wie ein senkrechtes Prisma mit den angegebenen Maßen. Also: $V=27000cm^{3}=27dm^{3}$
Der geschwungene Zylinder besitzt das gleiche Volumen wie ein senkrechter Zylinder mit den angegebenen Maßen. Also: $V\approx 1696,46cm^{3}\approx 1,7dm^{3}$

Zu deiner Lösung gehört auch der Rechenweg!

zurück