Nachricht für neue Nutzer.
Nachricht für engagierte Nutzer.
Lernpfad 8a - Volumina und Flächen/vermischte Übung: Unterschied zwischen den Versionen
Aus ZUM-Unterrichten
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 47: | Zeile 47: | ||
Insgesamt benötigt Familie Mertens also <math> 4 \cdot 18.000 cm^3= 72.000cm^3=72 dm^3=72L</math> Blumenerde. Sie brauchen also vier 20L-Säcke.|Lösung anzeigen|Lösung verbergen}} | Insgesamt benötigt Familie Mertens also <math> 4 \cdot 18.000 cm^3= 72.000cm^3=72 dm^3=72L</math> Blumenerde. Sie brauchen also vier 20L-Säcke.|Lösung anzeigen|Lösung verbergen}} | ||
<div class="center"><span class="brainy hdg- | <div class="center"><span class="brainy hdg-award04 fa-6x"></span></div> | ||
Version vom 19. Juni 2022, 09:49 Uhr
Info
Auf dieser Seite findest du vermischte Übungen Prismen und Zylindern. Du kannst jederzeit zu einer vorhergehenden Seite zurückgehen, wenn du eine Formel nachschauen möchtest oder sich bei den Übungsaufgaben noch allgemeine Fragen ergeben. Bearbeite die Aufgaben in deinem Heft unter der Überschrift "Übung". Notiere auch bei Applets bzw. Spielen deinen Lösungsweg und dein Ergebnis.
Übung 1
In dem folgenden Applet siehst du die Skizze eines Partyzelts. Bestimme zunächst, wie groß die Zeltplane dieses Zeltes ist. Berechne dann die Luftmenge, die in dem Zelt enthalten ist. Über den Button "anzeigen" kannst du dir verschiedene Maße anzeigen lassen. Sollte das Applet nicht richtig laden, klicke [1].

Übung 2
In der Tabelle sind jeweils zwei Größen eines Zylinders gegeben. Berechne die fehlenden Größen. Runde dabei auf zwei Nachkommastellen.
| Radius | Höhe | Mantel | Oberfläche | Volumen |
|---|---|---|---|---|
| 3 cm | 5 cm | 94,25 cm2 | 150,8 cm2 | 141,37 cm3 |
| 1,5 cm | 1,06 cm | 10 cm2 | 24,14 cm2 | 7,49 cm3 |
| 8 dm | 22 dm | 1105,84 dm2 | 1507,96 dm2 | 4423,36 m3 |
| 4 m | 2 m | 50,27 m2 | 150,8 m2 | 100,53 m3 |
Übung 3
Bestimme das Volumen der abgebildeten Prismen. Du kannst die einzelnen Skizzen vergrößern, indem du auf das Bild klickst.
Übung 4
Auf dem Bild siehst du zwei unterschiedliche Gläser. Das linke ist mit Saft gefüllt. Kann die Flüssigkeit vollständig in das rechte Glas umgefüllt werden?
Die Gläser haben die Form eines Zylinders. Berechne das Volumen der beiden Zylinder.
[cm3] [cm3]
In das rechte Glas passt etwas weniger Flüssigkeit rein. Da das linke Glas nicht komplett gefüllt ist und der Unterschied mit ca. 1 cm3 sehr gering ist, kann man den Saft vollständig umfüllen.Übung 5
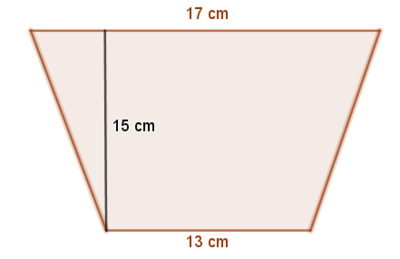
Familie Mertens möchte ihre vier 80cm langen Blumenkästen auf dem Balkon neu bepflanzen. Wie viel Säcke Blumenerde benötigt sie, wenn ein Sack 20L Erde enthält? Die Skizze zeigt den Querschnitt der Blumenkästen an.
Die Blumenkästen haben die Form eines Prismas, wobei die Grundfläche ein Trapez ist und die Höhe 80 cm beträgt.
1 L entspricht 1 dm3, also 1.000 cm3
Ein Blumenkasten hat folgendes Volumen: [cm3]
Insgesamt benötigt Familie Mertens also Blumenerde. Sie brauchen also vier 20L-Säcke.