Goldener Schnitt: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| Zeile 11: | Zeile 11: | ||
==Unterrichtsideen== | ==Unterrichtsideen== | ||
*''' | *'''Fächerverbindendes Unterrichten''': den goldenen Schnitt mit Zirkel und Geodreieck konstruieren (eventuell: Fächerverbindend mit der Mathematik) | ||
*'''Kunstgeschichte''': mithilfe eines "goldenen Zirkels" Bilder und Gebäude aus Renaissance und Antike analysieren | *'''Kunstgeschichte''': mithilfe eines "goldenen Zirkels" Bilder und Gebäude aus Renaissance und Antike analysieren | ||
*'''Kunstgeschichte''': eine Kompositionsskizze zu einem Werk zeichnen, den goldenen Schnitt nachweisen | *'''Kunstgeschichte''': eine Kompositionsskizze zu einem Werk zeichnen, den goldenen Schnitt nachweisen | ||
*'''Abstraktion, Fächerverbindendes Unterrichten''': | *'''Abstraktion, Fächerverbindendes Unterrichten''': Die Fibonaccireihe besprechen (eventuell fächerverbindend mit der Mathematik, Thema Wachstum). Eine "goldene Spirale" auf einem Blatt Papier konstruieren (DIN-A4 Blatt, Rechteck von 21x13cm zeichnen und mit Quadraten - 13x13cm, 8x8cm, 5x5cm, 3x3cm, 2x2cm, 1x1cm - füllen, mit dem Zirkel die Rundungen einzeichnen) und farbig ausmalen lassen. | ||
*'''Abstraktion''': ein abstraktes Bild konstruieren, das viele goldene Schnitt enthält | *'''Abstraktion''': ein abstraktes Bild konstruieren, das viele goldene Schnitt enthält | ||
| Zeile 28: | Zeile 28: | ||
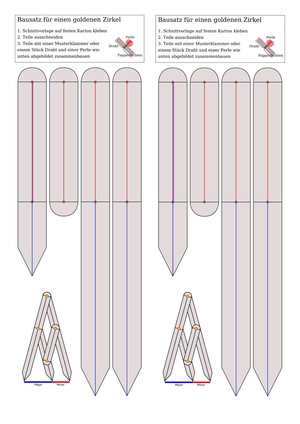
Der goldene Zirkel ist ein Proportionszirkel, mit dem man den goldenen Schnitt auf Bildern nachweisen kann. Aus Pappe kann dieser auch leicht selbst angefertigt werden. | Der goldene Zirkel ist ein Proportionszirkel, mit dem man den goldenen Schnitt auf Bildern nachweisen kann. Aus Pappe kann dieser auch leicht selbst angefertigt werden. | ||
[[Datei:GoldenerZirkel.jpg|mini|Goldener Zirkel, Instrument, das eine Strecke automatisch im goldenen Schnitt teilt.]] | [[Datei:GoldenerZirkel.jpg|mini|Goldener Zirkel, Instrument, das eine Strecke automatisch im goldenen Schnitt teilt.]] | ||
[[Datei:GoldenerZirkelBauanleitung.pdf|mini|verweis=Special:FilePath/GoldenerZirkelBauanleitung.pdf]] | [[Datei:GoldenerZirkelBauanleitung.pdf|mini|verweis=Special:FilePath/GoldenerZirkelBauanleitung.pdf|Die PDF kann direkt ausgedruckt werden. Wichtig ist dabei, darauf zu achten, dass die Datei beim Drucken nicht verzerrt wird. ]] | ||
| Zeile 38: | Zeile 38: | ||
Datei:Albrecht DÜRer - Melencolia I - Google Art Project.jpg|Albrecht Dürer: Melencolia, 1514 | Datei:Albrecht DÜRer - Melencolia I - Google Art Project.jpg|Albrecht Dürer: Melencolia, 1514 | ||
Datei:2003 Niemeyer-1.JPG|Jo Niemeyer, Skulptur at the Kunsthalle Villa Kobe in Halle | Datei:2003 Niemeyer-1.JPG|Jo Niemeyer, Skulptur at the Kunsthalle Villa Kobe in Halle | ||
Datei:Da Vinci Vitruve Luc Viatour.jpg|Leonardo da Vinci: Der Vitruvianische Mensch, 1492 | |||
</gallery> | </gallery> | ||
[[Kategorie:Kunst]] | [[Kategorie:Kunst]] | ||
Aktuelle Version vom 19. Januar 2022, 19:12 Uhr
Der goldene Schnitt ist ein Proportionsverhältnis zwischen zwei Strecken. Bilder oder architektonische Werke, die nach diesem System komponiert wurden, haben den Ruf, besonders harmonisch zu wirken. Besonders häufig wird der goldene Schnitt bei Renaissancewerken und in der Antike verwendet.
Definition
Als Goldener Schnitt (lateinisch sectio aurea, proportio divina) wird das Teilungsverhältnis einer Strecke oder anderen Größe bezeichnet, bei dem das Verhältnis des Ganzen zu seinem größeren Teil (auch Major genannt) dem Verhältnis des größeren zum kleineren Teil (dem Minor) gleich ist. [1]
Relevanz für den Kunstunterricht
Der goldene Schnitt ist eine wichtige Kompositionsmöglichkeit, die Schüler*Innen sowohl für eigene Werke als auch bei der Analyse von Bildern und Gebäuden anwenden können.
Unterrichtsideen
- Fächerverbindendes Unterrichten: den goldenen Schnitt mit Zirkel und Geodreieck konstruieren (eventuell: Fächerverbindend mit der Mathematik)
- Kunstgeschichte: mithilfe eines "goldenen Zirkels" Bilder und Gebäude aus Renaissance und Antike analysieren
- Kunstgeschichte: eine Kompositionsskizze zu einem Werk zeichnen, den goldenen Schnitt nachweisen
- Abstraktion, Fächerverbindendes Unterrichten: Die Fibonaccireihe besprechen (eventuell fächerverbindend mit der Mathematik, Thema Wachstum). Eine "goldene Spirale" auf einem Blatt Papier konstruieren (DIN-A4 Blatt, Rechteck von 21x13cm zeichnen und mit Quadraten - 13x13cm, 8x8cm, 5x5cm, 3x3cm, 2x2cm, 1x1cm - füllen, mit dem Zirkel die Rundungen einzeichnen) und farbig ausmalen lassen.
- Abstraktion: ein abstraktes Bild konstruieren, das viele goldene Schnitt enthält
- Fotografie: eigene Bilder fotografieren, in denen mit dem goldenen Schnitt gearbeitet wird (Da man hier notfalls auch nachträglich zuschneiden kann, fällt hier aufwändiges Konstruieren weg.)
Das Thema "Goldener Schnitt" eignet sich außerdem auch gut für Referate.
Unterrichtsmaterial: Goldener Zirkel
Der goldene Zirkel ist ein Proportionszirkel, mit dem man den goldenen Schnitt auf Bildern nachweisen kann. Aus Pappe kann dieser auch leicht selbst angefertigt werden.
Exemplarische Werke für die Analyse
Leonardo da Vinci: Das letzte Abendmahl, 1495-1498
Rafael: Sixtinische Madonna, 1513-1514
Albrecht Dürer: Melencolia, 1514
Jo Niemeyer, Skulptur at the Kunsthalle Villa Kobe in Halle
Leonardo da Vinci: Der Vitruvianische Mensch, 1492
_-_The_Last_Supper_(1495-1498).jpg)
.jpg)
