Prozente und Prozentrechnung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 31: | Zeile 31: | ||
|3=Beispiel}} | |3=Beispiel}} | ||
<body> | <body> | ||
<div id="ggbApplet"></div> | <div id="ggbApplet"></div> | ||
| Zeile 87: | Zeile 78: | ||
</script> | </script> | ||
</body> | </body> | ||
Version vom 20. August 2021, 21:12 Uhr
Herzlich willkommen im Lernpfad Prozente und Prozentrechnung!
Dieser Lernpfad soll dir dabei helfen, dein Wissen aus der Bruchrechnung auf die Prozentrechnung zu übertragen und deine Vorstellung von Prozenten auf- bzw. auszubauen.
Das Schöne daran ist, dass du vieles von dem, was du bereits aus der Bruchrechnung kennst, hier direkt anwenden kannst.
Der Begriff "Prozent" heißt dabei nichts anderes als "von Hundert". Du hast es also im Prinzip mit nichts anderem zu tun, als einem Bruch, dessen Nenner immer 100 ist. Es gibt also keinen Grund, vor der Prozentrechnung Angst zu haben!
Also: Leg los!
Wiederholung: Bruchteil, Anteil und Ganzes
In diesem Beispiel schauen wir uns noch einmal eines Kreises an.
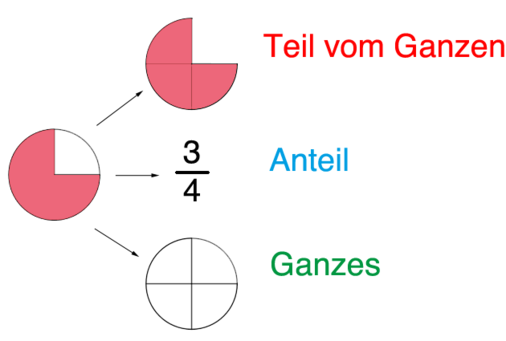
|
|
In der Prozentrechnung gibt es nun andere Begriffe für das, was du bereits aus der Bruchrechnung kennst. |
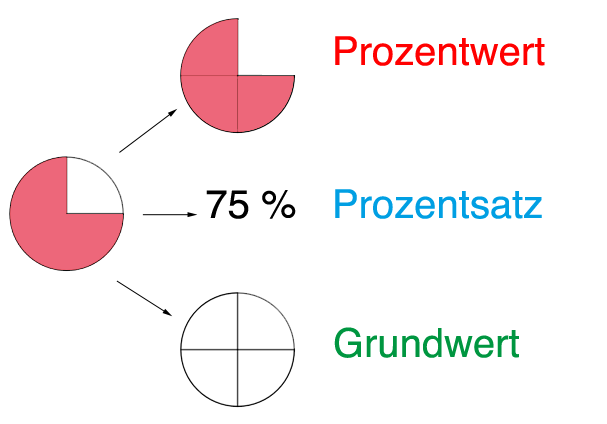
<body> <script> var parameters = { "id": "ggbApplet", "width":1920, "height":1017, "showMenuBar":true, "showAlgebraInput":true, "showToolBar":true, "customToolBar":"0 73 62 | 1 501 67 , 5 19 , 72 75 76 | 2 15 45 , 18 65 , 7 37 | 4 3 8 9 , 13 44 , 58 , 47 | 16 51 64 , 70 | 10 34 53 11 , 24 20 22 , 21 23 | 55 56 57 , 12 | 36 46 , 38 49 50 , 71 14 68 | 30 29 54 32 31 33 | 25 17 26 60 52 61 | 40 41 42 , 27 28 35 , 6", "showToolBarHelp":true, "showResetIcon":false, "enableLabelDrags":false, "enableShiftDragZoom":true, "enableRightClick":false, "errorDialogsActive":false, "useBrowserForJS":false, "allowStyleBar":false, "preventFocus":false, "showZoomButtons":true, "capturingThreshold":3, // add code here to run when the applet starts "appletOnLoad":function(api){ /* api.evalCommand('Segment((1,2),(3,4))');*/ }, "showFullscreenButton":true, "scale":1, "disableAutoScale":false, "allowUpscale":false, "clickToLoad":false, "appName":"classic", "buttonRounding":0.7, "buttonShadows":false, "language":"de", // use this instead of ggbBase64 to load a material from geogebra.org // "material_id":"RHYH3UQ8", // use this instead of ggbBase64 to load a .ggb file // "filename":"myfile.ggb", "ggbBase64":"UEsDBBQAAAAIAEC5FFP7dINnCwUAAP0lAAAXAAAAZ2VvZ2VicmFfZGVmYXVsdHMyZC54bWztmk9z2jgUwM/bT+HRafcQsAEDycTppJ3Z2cykaWeT2dmrMMJoIySvJQeTT98nydgmxCmYtEBTDshP1t/fe5KeJJ+/z2bMeSCJpIIHyGu5yCE8FGPKowClanIyRO8v3p1HRERklGBnIpIZVgHydcoiH0itvt/XcTiOAxQyLCUNkRMzrHSWAInJhFFOkONkkp5xcYNnRMY4JLfhlMzwtQixMmVNlYrP2u35fN5a1toSSdSGgmU7k+N2FKkWhMiBpnMZoPzhDMpdyT3vmnwd1/Xa/366tvWcUC4V5iE0BLo1JhOcMiXhkTAyI1w5ahGTAMWCcoUchkeEBeiLlpzfJwkhfyAnzwS0XHTx7rdzORVzR4z+IyHEqSSFovN8RmjrNPD6o2AicZIADQbIAbg6GAWo4/sAjcVTHCDXJmZ4QRLnAUMJeQxOlQhNfhM7wUzmBZuaPokxsW96eXpOQUuA05GKgD7cloccGRMyhlajvI/wAOpZGE1XSgyFSMbSyQJ0g2+Qs8jDRxuaJIbOLX3MK/WrsWrB8mjT9vN2DnYzxGMSEz6GRCucvUac+0PDWQfAWQfHjTmv9Pth7h8J5j1AhqG+LeXPvMq204it14HJAbpkwl+TxQrfK/43iaDVVcrd46F8FIxXbbjXiC74BNAf+D9KsiaJZSj1P/g2YhYzkr0ieOsX5RCvjVBA7zTzMarQtVO2jykD6m0IXQOx+NSUhvecSHDzwHKKcvXDX3QMK5ipT4AfSRWU5A2GtgTyP19RGgWdUUjzsiImKQ91rwq4H9PkoaqNbs/dhz7KMhuPgBpl7Eq6nqUkkZYKLrdLuTTtZm7dWzdtkSqma77iCrZfQA3aKtc6d09IfAdFfeZ3CeZS78FWbalecwlevKQ1/xi09tZ0tpy5+ANOCk1UtdbMM6pdu1tgBntW3RbTeBXE7k7MQZnvlra5kxH1mw39jtt7nl5rcMBG9ADdEyWGf3KxdAV+OWZNZsJn/GmcKCIp5t/anbBFVBnTX5ZyoZGB1cjubdx6/+h3jVZ9KO2JhXuu/Xm9U9fz+nAMsHdFv4x4ZS+iGduIErJ12n485IMdOPU8Q8H1GfhyL2GlgmTvp5tAXmHbRiPC7cwr4aLANckWEEDmRy3pG4bMM/ICAnj7qAOINvmh6QnNnEub49ImvOzYoGuDng38AlGzvaJRbgxzV8VXfrJE9JptcA5hOnnTSv8B/jpPZySpTA43S7kwHt9OD1BeWj1F2mgyqLOTequQjI7BhGYUlHQC2pthcAO0vz+SgqUKLung7ouXl3TWjOd0rKbawYO6JzTT5mLLdKYioY+Cq4KGo0fBJTPXeSsHGs+ZT+cl/3XFWHeboDGPWDkaL61UasCe2ZtETw/znlNMlSE0xCDstzrDrjf0u+7AG5z6w/6GSL1hidS+2Jjoun2ANexuIVuNc1Dg+jjHSVielIL7XLPeuN6g53c7px3fOz3twQNU8tobwj+LiHJzc4gHe8YC1pJ+tzM7JsJUlifRVioIgUn+ZA4LTjPKKE4Wu1n7VowVyUqX4c4IlQ8KDhBxfVcAfFQ27cpKlVt725kJBYocvvaAswRTCeUfcHgfJSLluW1XF6JX6Xq+UBziucJICEZgs7vs1oelXLkrXlv66wDlq+0+xx98VRPej0S2slp947pLliPg2giVG9xnRsDmvVxf6U72bgpNzui2uliscVGqCmhXPnRqL7+quvgKUEsDBBQAAAAIAEC5FFMwuba3fAMAAE8RAAAXAAAAZ2VvZ2VicmFfZGVmYXVsdHMzZC54bWztmM1u2zgQgM/bpyB4ryXZkhIFUQqje9gF2iKLXvbKUGObuzKpkrRl5dX6Dn2mDn/iyG0S1EESoEV98PBHM0N+MxqJOn+zW7dkC9oIJWuaTVJKQHLVCLms6cYuXp/SNxevzpeglnClGVkovWa2poW7cq+HvUlZlG6MdV1NecuMEZySrmXWqdRULRatkEAJ2RlxJtUHtgbTMQ4f+QrW7J3izHpbK2u7syTp+35y43Wi9DJBwybZmSZZLu0EJSW4dGlqGhtnaPdAu595vWmaZsm/798FP6+FNJZJjgvBbTWwYJvWGmxCC2uQltihA9yAkoLP0EfLrqCt6d/S4l6BuyUSvtFb1I/KNZ1lRUovXv1xzpXSjSFqV1MkoYYgroPoES8iC3PbMLcNc30Y7MNg7wcTZ9CsVE/U1X/ouKZWb9BrXJDv+Gtw+q1qlSa6plP0gHHLUpRXKKspBqTtVgwtTrI0/LK8SrOszKZBv2UDaLJlaDR6ZRuruDfpRxesNdGXd/5eNRBm8ni9FJgTjoyxgNFH56YDaHwr8MRtYSoMPqvG9jAjPtqhBWJXgv8vwWA8i5GSa/wlmgZccgYdEEuQWySitMFkSr2XAQVefu16Lgt3me8PKHD22gkc9vq4VC12ZB405uHC+TSIWRB5EMUeCXySYZ3G/de0YxrzFw1xN3+exOz5Lo/YTpjZn/uozWN3lDrpzKfOsZHG5SFK/Mcwu7suBvm5QorZ87xBvZ8viW3AXX/5/DBuf2dypi0YweTo/n3rJr4lX/4M5J+T+/0g0b6EEb9L3z/gh3X1UfyqygOcZigRoZf7GlU8FcZYikNhDXU11tq9yQVzT7no5d7qeBfUyPJoqKodVtBoJW+5joZu0c4i2sfcSceGIytmPh5FeGSMMnqSRyRFVaZ5mT9ZbB6b4keRnWu+EmtogB2ixcC+FNppFh7H+YlH68SvwfZywIossDqMub5cyvqSgYuvAtfpL5Ozl1qY9SHV7AWplqEwB6oV9n5CqhLsfp8fXHtcVYvfVfUYlp82rPFvYHGr/9z0x0xDgj5laSzzyv1Oyqw4zXI80jwRoOc4bNx51HCD4TwxBHGNIho89vRB5mUQJ0GcBlHdezIR664VXNiHQ2s2eoFn77telePUYZTzx0UZ9e58WZ6c/Gja3xp+kdflsdKDb3bJ6NNBcvOd4uIrUEsDBBQAAAAIAEC5FFPWN725GQAAABcAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwMEFAAAAAgAQLkUU2Xa+BHICQAA3CwAAAwAAABnZW9nZWJyYS54bWzdWu1y28YV/e08xQ5m0rFbkcTik3RJZyRbsjOjJJrI7XT6DwSW5FYgwAKgRHryOH2TvljO3QVAUJBM0ZRjKbLJBRYXd3fPPfdjQQx/WM1jdi2yXKbJyOBd02AiCdNIJtORsSwmnb7xw5vvhlORTsU4C9gkzeZBMTJckqzvw1nXcz3qCxaLkRHGQZ7L0GCLOCjolpGRTiaxTITBZAR56/TUP/OszonP3Y5zZtmdY+74HXNw6vGzd/7x2empwdgql6+T9OdgLvJFEIrLcCbmwXkaBoUadVYUi9e93s3NTbeaXzfNpj1MIe+t8qg3nY67aA2GRSb5yCgPXkPv1t03trrPMk3e+9dP53qcjkzyIkhCTJkAWMo3370Y3sgkSm/YjYyKGeAaWFjxTMjpDJBwk/sG65HYAsAsRFjIa5Hj5sapWn4xXxhKLEjo+gt9xOJ6ZQaL5LWMRDYyzC4f+APuNf4MlmZSJEUpzPWgLSXob2jxTMvs25u/u5UMe9WchtdS3OjJ0ZE2G7cMVqRpPA5IJ/uNceaa+DA+YEfM89FjMe4yBz199PjMpj6XO8xmJMJt5jhoHermHq7QZXy7rsk4xxVmmcyymMWZZePUdZkLMZ/utSDrDZQ+Ex+SxozwsanPtvFRfbaDj0VHUORqNZiHa3vqyFXffboHo7gY7zemLqHPGWA46nB9zmzMBOe+yaAX6jFjtRrHZPSfM4cGsXxm9ZnSqvSbwOha5nIci5ExCeKcOJ9MMrC4Ps+LdSwUiGVHw2pH+AcJ+Qnirgl+ac4Rv8wj+nj4OHRBW722Du6qxy2y5b7DghF6UM5dUOyhozrbjAABQDSCxQS4qoHZqBc8oVOTzIFGQWeaRAY0rpYBrHQKaFWjZRRh0GCCh+FaLdDeB9V+Y32QI76iISqisRnNGweYPzVOeerpU0VyE2TVvUQ5NGAweHzgYmpr7bUYxxwgRD2YJfr63Rh6AOb2sD4+cOTWsE2P2HfMzUL7UFwE45FxfP7+9OTX4z0840C078TaxVrpv/q0hrT3igItoL9gRG/LEx9nwQ5h/rDhuQVC/MFj+sSIdvDRLTxVtY9jiMEOQwx7Vb4cljNi+YxkS74XYo4CxGS+zTwVPFTiRMZExtDZ07eY7zKfQkeVQ5Hz+syjtkyklEb7W4nUpTTbyKYedSJjUaRhKhHqtGo5VWbFscqtlHe3cyuSoLPJg5ggqeKMIXszj4JXmRAxC6tOiRamjwzoMaRN12IeBch7siPKwTSXNbAzEaNULE2gMJTJYlls4RbOqVxSh0UK6SBWZV4pH6Xh1UmNdKlJBDmKsY1alDSb8kuXOFvV2YthHIwFatPpJdGAsesgJgdSI0zSpGBVXvSob9hTpeBQLMNYRjJI/gm7V/XSz8v5WGTgGw5TWqRSQrezumZU2bWqGQfwWiUTpmkWXa5z8ISt/i0y3D1wur7joPjzbBs1IHcNttZXUPt0uef00WvaLhq4fh4GxHDH7LrOwLYt3+YofQa4554rllrOi6G4vhRFgeXnLFgJkFTDPc3Iw0oY6eTH/CSNN12LVCbF22BRLDO1V0CczmhNx8k0FgpJZWSU0uHVOF1dKggxptL1cb3AWafEZzx9m8ZpxuB/lotVQptqEeqpVTI0tVoKPgcZfEOiNBRpra+jLlcSqoUMtUqKdiDaynqpmKBeZ6klWMlcRRbobtJQMYTK8mUii/PqpJDh1WalJK/tX2G4rbIUOVjlsHeLesPSKSoiztNIaBLbWn7r+vBKZImINecS2H2ZLnMtri2rZr3MxUVQzI6T6FcxhcNeBBQwC0xEi27WF4lQznGj7i9xDogE/8DCdG8kppmo8NCT0VYoZ8nyRSaCKJ8JAZ8obaE9YiOmuoe9avpDlAKxUKlgLhFQOjD1PFipYgNehFih2DXMw0wuiN5sjLB+JTYMjmROKuoOkgYkOdaG2JAmMEZBhrjI0k/YKKFfyIlIsMVdFrMUNIOKoIAA9nJDEYs5hFihmJ0s5yKj/W9pZam2e1jGslxMRWuyMEvH/0E0ukWMDcK4fA/zWRAvZoHaI5r6jzsDk3MP+zTN92BN4agR0JT2n7YZgmmATxBUQEKtwhEqKePpoIVD6uq6vmPavuO7po99kY24swbiXdvnjode2xs4lu3DohO5akANuOQnsK2mjqL2saZCc60bBy1mcAVsRclLKc0rXMuDDzKKhEoiJdvAQGWxyvAglKDhcVTfiEcRaxWpGjQPEb/oPoXFgo3Y99fs+9LJtEF3mja5bVrM9hua9pfJJBcFGatDDwpgnQ4vU8xu0yPmahfCQcvyHKb3vb5vwe4ctR5Uu12L983+wPFMbvum9zztfv7//yVTwSKRs8vSx/PXxIRw3qLCCoEKT7Zwa2nLdyg4Vhj7ZXLEzFfVsCo56upjmz3lhfrmFlGquvhzTOFkH0pv1JZJsubLAx2/GWRzZWFABZPi+1MNsJotZe4yaDV7W4F5g1KYzudBErFE1dg/JpQ2sDi1WF3iBebIWB0jM2LefGSs1aFe57KoBI613lLbDiiPvwxK2sUCSWoAJDWH4rgbxtIdd8LYJttJRTbziHXsW2zbRbaTL0PIxwMDIETNYVS77a2IbG1/xcGd/noL3g4izcE0beP7tuHMLXx3evPbbwxwy5cfBaVtZ75I4/U01Tlv48p4FENuDHoGlkIxsCm43Xboa1iX5LB9I7mxlkMqDRzUiLu8XQ9cYQld9+YNIHhP2mApfkeQBbDhfn9Xmm7wr2mvaouiM7VLa6pT9UPLrjYXtxabiymd1TMJ2sw6bKZ7eu5yJWMZZOvWNmFDOVCtDnuVsoNtA+7EFAvqFAJfbe9VroRY0Ibyl+RjFiQ5/dy0vUl5ONDjpw+0dm3ycCBtP1+ow6cPNcXPmtTPGOro6UNdJqyS1k8a6lbV8L6qGl6uXr59xf7KJOvR7zyvjtgaHfuWEe+fTBnhdumR41ertvALf13N3t467QLp9JvvnB6znH2MTVcb3w+H7BY+/KkA/koMPmt4/rvbnv9ub88/e3Ke//hPA+7eQCAU0MYAeNLGAAGVNgYf2hsIPNslOSBCchMtN9UbiNmeGwjrW20g9IM+7oKTZC8TD1HrHQQeoX2VHYT4shLgM1P9WjWAot5TrwE+i/XkGWDdrGw73APmzxXt6TNAu0xCFbWfN+CzZwD41s7tSUeSVk3xUawKjK7qir/8d5kWf9ff7G+stcF4hc6mzF0lRgF9tW208gf8OsXENb369tAfqfazIF6rzYoLqhvIVla3T6+32rbvenh50qaXaMlbnK7r9i0fr9jiBYe+5eDXrKoWaSKIhL/5yVa9nlG+Cvzmd1BLAQIUABQAAAAIAEC5FFP7dINnCwUAAP0lAAAXAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9kZWZhdWx0czJkLnhtbFBLAQIUABQAAAAIAEC5FFMwuba3fAMAAE8RAAAXAAAAAAAAAAAAAAAAAEAFAABnZW9nZWJyYV9kZWZhdWx0czNkLnhtbFBLAQIUABQAAAAIAEC5FFPWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAPEIAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAAAAgAQLkUU2Xa+BHICQAA3CwAAAwAAAAAAAAAAAAAAAAAPgkAAGdlb2dlYnJhLnhtbFBLBQYAAAAABAAEAAgBAAAwEwAAAAA=", }; // is3D=is 3D applet using 3D view, AV=Algebra View, SV=Spreadsheet View, CV=CAS View, EV2=Graphics View 2, CP=Construction Protocol, PC=Probability Calculator DA=Data Analysis, FI=Function Inspector, macro=Macros var views = {'is3D': 0,'AV': 1,'SV': 0,'CV': 0,'EV2': 0,'CP': 0,'PC': 0,'DA': 0,'FI': 0,'macro': 0}; var applet = new GGBApplet(parameters, '5.0', views); window.onload = function() {applet.inject('ggbApplet')}; applet.setPreviewImage('data:image/gif;base64,R0lGODlhAQABAAAAADs=','https://www.geogebra.org/images/GeoGebra_loading.png','https://www.geogebra.org/images/applet_play.png'); </script> </body> |



