Vektorrechnung/WHG Q1 Vermischte Übungen zu Vektoren: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 16: | Zeile 16: | ||
====Der Weg durch das Labyrinth - Vektoren zeichnen==== | ====Der Weg durch das Labyrinth - Vektoren zeichnen==== | ||
*Zeichnen Sie mit Hilfe von Vektoren einen lückenlosen Weg durch das Labyrinth vom Start- zum Zielpunkt ein. Geben Sie dazu im Eingabefeld die Vektoren einzeln in folgender Schreibweise ein: ''Vektor((<math>a_1</math>, <math>a_2</math>), (<math>b_1</math>, <math>b_2</math>))'' <math>-</math> Dies beschreibt den Vektor vom Punkt <math>A(a_1|a_2)</math> zum Punkt <math>B(b_1|b_2)</math>. | *Zeichnen Sie mit Hilfe von Vektoren einen lückenlosen Weg durch das Labyrinth vom Start- zum Zielpunkt ein. Geben Sie dazu im Eingabefeld die Vektoren einzeln in folgender Schreibweise ein: ''Vektor((<math>a_1</math>, <math>a_2</math>), (<math>b_1</math>, <math>b_2</math>))'' <math>-</math> Dies beschreibt den Vektor vom Punkt <math>A(a_1|a_2)</math> zum Punkt <math>B(b_1|b_2)</math>. | ||
| Zeile 38: | Zeile 39: | ||
<br> | <br> | ||
==== | ====Parallelogramm im Raum==== | ||
Überprüfen Sie, ob die Punkte <math>A(2|3|4)</math>, <math>B(4|-1|2)</math>, <math>C(3,25|-0,3|8)</math> und <math>D(1,25|3,7|10)</math> die aufeinanderfolgenden Ecken eines Parallelogramms <math>ABCD</math> sind. | |||
{{Lösung versteckt| | |||
[[Datei:0 Abbildung 4.png|200|center|Abbildung 4]] | |||
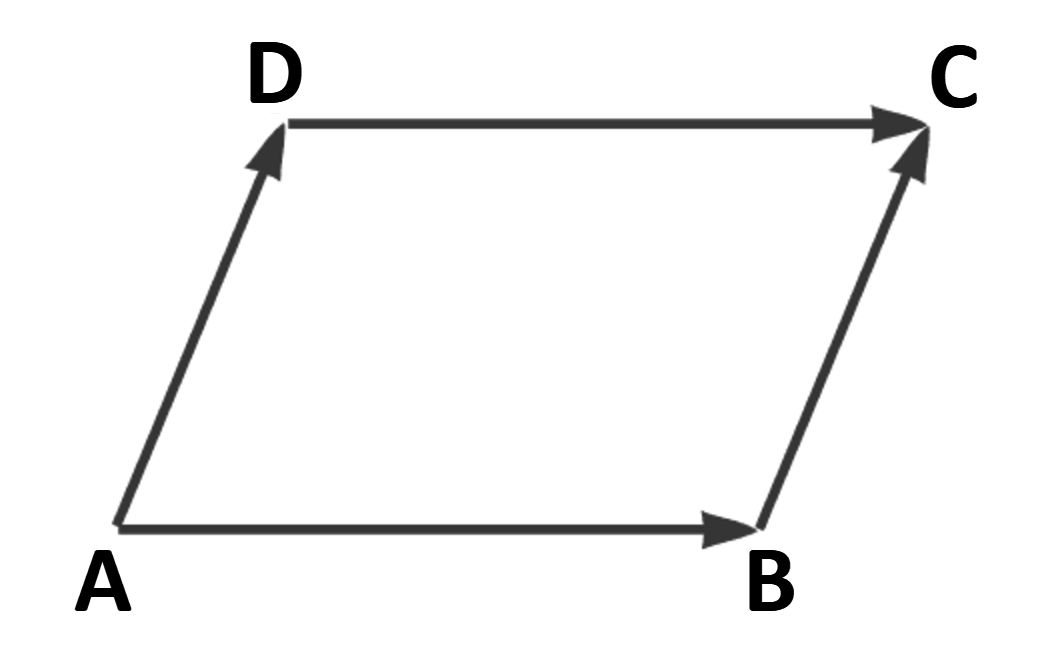
Die Abbildung verdeutlich, dass es genügt zu überprüfen, ob <math>\vec{AB}=\vec{DC}</math> (bzw. <math>\vec{AD}=\vec{BC}</math>) gilt: | |||
<math>\vec{AB}=\begin{pmatrix}4-2\\-1-3\\2-4\end{pmatrix}=\ begin{pmatrix}2\\-4\\-2\end{pmatrix}</math>; <math>\vec{DC}=\begin{pmatrix}3,25-1,25\\-0,3-3,7\\8-10\end{pmatrix}=\ begin{pmatrix}2\\-4\\-2\end{pmatrix}</math>; also gilt <math>\vec{AB}=\vec{DC}</math>. Folglich sind <math>A</math>, <math>B</math>, <math>C</math> und <math>D</math> die Ecken eines Parallelogramms. | |||
}} | |||
<br> | <br> | ||
<br> | <br> | ||
{{Fortsetzung|weiter=zurück zur Übersicht|weiterlink=WHG_Q1_Vektorrechnung|vorher=Definition (Orts-)Vektor|vorherlink=WHG Q1 Vektorrechnung/WHG Q1 Definition (Orts-)Vektor}} | {{Fortsetzung|weiter=zurück zur Übersicht|weiterlink=WHG_Q1_Vektorrechnung|vorher=Definition (Orts-)Vektor|vorherlink=WHG Q1 Vektorrechnung/WHG Q1 Definition (Orts-)Vektor}} | ||
Version vom 21. September 2020, 09:21 Uhr
Auf dieser Seite finden Sie vermischte Übungen zum Rechnen mit Vektoren.
Im Rahmen unterschiedlicher Aufgabentypen können Sie Ihr neu erworbenes Wissen vertiefen.
Ortsvektoren
Bestimmen Sie den Ortsvektor des Punktes , indem Sie Anfangs- und Endpunkt des Pfeiles bewegen.

Der Weg durch das Labyrinth - Vektoren zeichnen
- Zeichnen Sie mit Hilfe von Vektoren einen lückenlosen Weg durch das Labyrinth vom Start- zum Zielpunkt ein. Geben Sie dazu im Eingabefeld die Vektoren einzeln in folgender Schreibweise ein: Vektor((, ), (, )) Dies beschreibt den Vektor vom Punkt zum Punkt .
- Begründen Sie anschließend, welche der Pfeile zum selben Vektor gehören.

Vektoren im Koordinatensystem
Gegeben ist der Vektor .
- Zeichnen Sie drei Pfeile, die den Vektor repräsentieren, in ein Koordinatensystem.
- Es gilt: mit bestimmen Sie die Koordinaten von .
- Es gilt: mit bestimmen Sie die Koordinaten von .
- -
- Geht man von aus drei Einheiten in Richtung der -Achse und anschließend eine Einheit in Richtung der -Achse, so erreicht man : bzw. .
- Geht man von aus drei Einheiten in Richtung der -Achse und anschließend eine Einheit gegen die Richtung der -Achse, so erreicht man : bzw. .
Parallelogramm im Raum
Überprüfen Sie, ob die Punkte , , und die aufeinanderfolgenden Ecken eines Parallelogramms sind.
Die Abbildung verdeutlich, dass es genügt zu überprüfen, ob (bzw. ) gilt: Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \vec{AB}=\begin{pmatrix}4-2\\-1-3\\2-4\end{pmatrix}=\ begin{pmatrix}2\\-4\\-2\end{pmatrix}} ; Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \vec{DC}=\begin{pmatrix}3,25-1,25\\-0,3-3,7\\8-10\end{pmatrix}=\ begin{pmatrix}2\\-4\\-2\end{pmatrix}} ; also gilt . Folglich sind , , und die Ecken eines Parallelogramms.