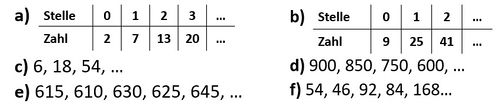Muster erkennen und geschickt fortsetzen/Vertiefungsaufgaben: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 57: | Zeile 57: | ||
'''b)''' Hinter den Schubladenschränken verstecken sich Zahlenfolgen. Welche Zahlen müssen in den Schubladen des nächsten Schrankes stehen? Überprüfe dein Ergebnis, indem du auf den Schrank in der App klickst. | '''b)''' Hinter den Schubladenschränken verstecken sich Zahlenfolgen. Welche Zahlen müssen in den Schubladen des nächsten Schrankes stehen? Überprüfe dein Ergebnis, indem du auf den Schrank in der App klickst. | ||
{{Lösung versteckt|1= | |||
Findest du eine Regelmäßigkeit, wenn du das arithmetische Mittel des ersten, zweiten und dritten Schrankes als Zahlenfolge nebeneinander schreibst? | |||
Jetzt untersuche auch die Zahlen, die jeweils in den Schubladen auf gleicher Höhe stecken! Setze auch diese Zahlenfolge fort! | |||
|2=Tipp zu Aufgabenteil b)|3=Tipp ausblenden}} | |||
'''c)''' Beschreibe die Regelmäßigkeiten aus Aufgabenteil b) mit Worten. | '''c)''' Beschreibe die Regelmäßigkeiten aus Aufgabenteil b) mit Worten. | ||
'''d)''' Den linken Schrank mit den Zahlen 3, 4, 8, 9 zählen wir als 0. Schrank. Berechne die Zahlen im Schrank an der 10. Stelle mithilfe von Termen! Überprüfe dein Ergebnis wieder mit der App! | '''*d)''' Den linken Schrank mit den Zahlen 3, 4, 8, 9 zählen wir als 0. Schrank. Berechne die Zahlen im Schrank an der 10. Stelle mithilfe von Termen! Überprüfe dein Ergebnis wieder mit der App! | ||
'''*e)''' Erfinde selbst einen ähnlichen Schrank. Entscheide dabei selbst, welche Regelmäßigkeiten zwischen Zahlen vorkommen. | '''*e)''' Erfinde selbst einen ähnlichen Schrank. Entscheide dabei selbst, welche Regelmäßigkeiten zwischen Zahlen vorkommen. | ||
{{H5p-zum|id= | {{H5p-zum|id=4365|height=300}} | ||
|Üben}} | |Üben}} | ||
Version vom 20. Mai 2020, 14:46 Uhr
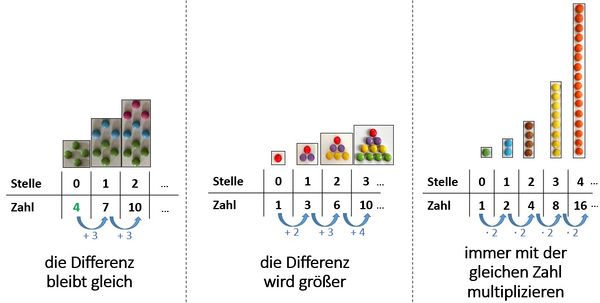
Um eine Regelmäßigkeitn zu erkennen, musst du immer die Veränderung zwischen den benachbarten Zahlen untersuchen.
Im ersten Beispiel ist die Differenz zwischen benachbarten Zahlen immer gleich. Hier kannst du mit einem Term zu einer Zahl an einer bestimmten Stelle "hinspringen". Beispiel:
Den Term für eine x-beliebige Stelle schreibst du auf, indem du anstatt einer bestimmten Stelle einfach "x" als Platzhalter schreibst. Für "x" kannst du dann jede Stelle einsetzen und so die Zahl an dieser Stelle ausrechnen.
Bearbeite diese Aufgabe in deinem Hefter!
a) Beschreibe jeweils die Regelmäßigkeiten in den Zahlenfolgen mit einem Satz und setze die Zahlenfolgen um drei Zahlen fort.
b) Schreibe einen Term mit "x" für die Zahlenfolge (b) auf. Erkläre, warum du für die anderen Zahlenfolgen keinen solchen Term aufstellen kannst.
c) Schreibe eine Zahlenfolge für den Term auf.
Für manche Fragen kann es helfen, dir Notizen zu machen!
Für ausgewählte Fragen im Quiz, sollst du auch etwas in deinen Hefter schreiben. Dies ist dann in der jeweiligen Frage gekennzeichnet!
Bearbeite diese Aufgabe in deinem Hefter!
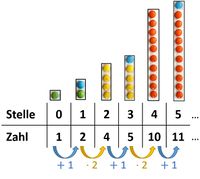
a) Berechne jeweils das arithmetische Mittel der Zahlen in einem Schubladenschrank. Was fällt dir dabei auf?
b) Hinter den Schubladenschränken verstecken sich Zahlenfolgen. Welche Zahlen müssen in den Schubladen des nächsten Schrankes stehen? Überprüfe dein Ergebnis, indem du auf den Schrank in der App klickst.
Findest du eine Regelmäßigkeit, wenn du das arithmetische Mittel des ersten, zweiten und dritten Schrankes als Zahlenfolge nebeneinander schreibst?
Jetzt untersuche auch die Zahlen, die jeweils in den Schubladen auf gleicher Höhe stecken! Setze auch diese Zahlenfolge fort!c) Beschreibe die Regelmäßigkeiten aus Aufgabenteil b) mit Worten.
*d) Den linken Schrank mit den Zahlen 3, 4, 8, 9 zählen wir als 0. Schrank. Berechne die Zahlen im Schrank an der 10. Stelle mithilfe von Termen! Überprüfe dein Ergebnis wieder mit der App!
*e) Erfinde selbst einen ähnlichen Schrank. Entscheide dabei selbst, welche Regelmäßigkeiten zwischen Zahlen vorkommen.
Die italienische Mathematiker Leonardo von Pisa, auch bekannt als "Leonardo Fibonacci"
Künstlerische Darstellung der Fibonacci-Zahlen und der "goldenen Spirale" im Züricher Hauptbahnhof
Wo finden wir die Fibonacci-Folge in der Natur außer bei der von Fibonacci beschriebenen Vermehrung von Kaninchenpopulationen? Was hat die oben abgebildete Spirale im Züricher Hauptbahnhof damit zu tun? Diese Fragen kannst du dir von Lehrer Schmidt beantworten lassen - folge dazu diesem Link zu Lehrer Schmidts Erklärung
